Bài viết bao gồm đầy đủ lý thuyết về hai đường thẳng song song. Trong bài còn có các dạng bài tập áp dụng và lời giải chi tiết giúp các em có thể nắm chắc và hiểu sâu bài học.
LÝ THUYẾT VÀ BÀI TẬP VỀ HAI ĐƯỜNG THẲNG SONG SONG
I/ Lý thuyết
1. Nhắc lại kiến thức lớp 6
+) Hai đường thẳng song song là hai đường thẳng không có điểm chung.
+) Hai đường thẳng phân biệt thì cắt nhau hoặc song song.
2. Dấu hiệu nhận biết hai đường thẳng song song
+) Ta thừa nhận tính chất sau:
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì:
a) a và b song song với nhau
b) Hai góc so le trong còn lại bằng nhau
c) Các góc đồng vị còn lại bằng nhau.
+) Hai đường thẳng a, b song song với nhau được kí hiệu là a // b.
+) Khi a và b là hai đường thẳng song song ta còn nói: Đường thẳng a song song với đường thẳng b, hoặc đường thẳng b song song với đường thẳng a.
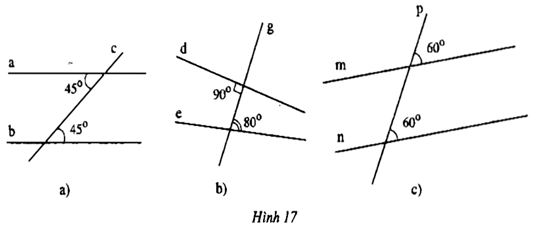
VD1: Xem hình 17 (a, b, c). Đoán xem các đường thẳng nào song song với nhau.
Giải:
Các đường thẳng song song với nhau là a và b ; m và n
VD2: Thế nào là hai đoạn thẳng song song?
Trong các câu trả lời sau, hãy chọn câu đúng:
a) Hai đoạn thẳng song song là hai đoạn thẳng không cắt nhau.
b) Hai đoạn thẳng song song là hai đoạn thẳng nằm trên hai đường thẳng song song.
Giải
a) Sai.
b) Đúng.
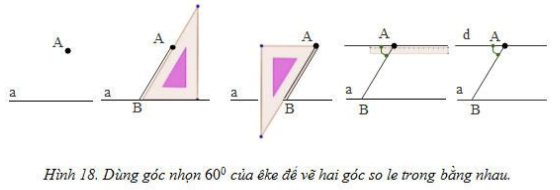
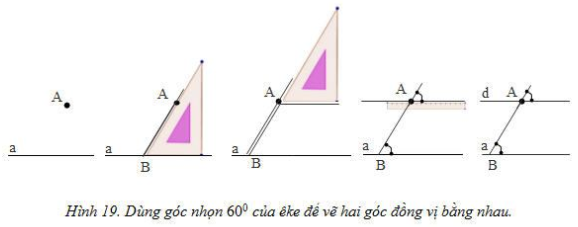
3. Vẽ hai đường thẳng song song
Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Hãy vẽ đường thẳng b đi qua A và song song với a.
Một số cách được minh họa ở hình 18, 19:
II/ Bài tập
Bài 1:
Điền vào chỗ trống (…) trong các phát biểu sau:
a) Hai đường thẳng a, b song song với nhau được kí hiệu là …
b) Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì …
Giải:
a) Hai đường thẳng a, b song song với nhau được kí hiệu là a // b.
b) Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a song song với b.
Bài 2:
Làm thế nào để nhận biết a // b?
Trong các câu trả lời sau, hãy chọn câu trả lời đúng?
a) Nếu a và b cắt c mà trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a // b.
b) Nếu a và b cắt c mà trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a // b.
c) Nếu a và b cắt c mà trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì a // b.
Giải
Để nhận biết hai đường thẳng song song thì phải dựa vào định nghĩa hoặc dựa vào tính chất.
a) Đúng b) Đúng c) Đúng
Bài 3:
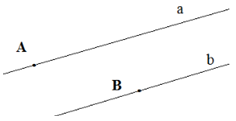
Cho hai điểm A và B. Hãy vẽ một đường thẳng a đi qua A và đường thẳng b đi qua B sao cho b song song với a.Giải:
Qua A, dùng êke vẽ đường thẳng a bất kì. Thế thì bài toán đưa về trường hợp vẽ đường thẳng b đi qua B và song song với a. Ta có thể dùng một trong ba góc của êke để vẽ hai góc so le trong bằng nhau hoặc hai góc đồng vị bằng nhau.
Bài 4:
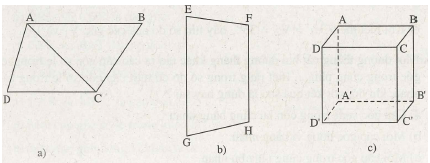
Kiểm tra xem trong các hình dưới, các đoạn thẳng nào song song với nhau
Giải
Hình a: AB // CD
Hình b: EG // FH
Hình c: AB // CD // A’B’// C’D’
AD // BC // A’D’ // B’C’
AA’ // BB’ //CC’ // DD’
Bài 5:
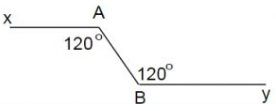
Vẽ cặp góc so le trong xAB, yBA điều có số đo bằng 120 độ. Hỏi đường thẳng Ax, By có song song với nhau không? vì sao?
Giải:
Ta có hình vẽ như sau:
Ta có Ax và By cắt đường thẳng AB và tạo ra một cặp góc so le trong bằng nhau. (left( {widehat {xAB} = widehat {yBA} = {{120}^0}} right))
Vậy Ax // By (theo dấu hiệu nhận biết hai đường thẳng song song).
Bài 6:
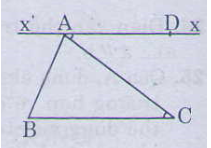
Cho tam giác ABC. Hãy vẽ một đoạn thẳng AD sao cho AD=BC và đường thẳng AD song song với đường thẳng BC.
Giải:
Cách vẽ:
– Đo góc (widehat C)
– Vẽ góc (widehat {CAx} = widehat C)
– Khi đó ta được đoạn thẳng BC, đo độ dài BC
– Trên tia Ax đặt đoạn thẳng AD có độ dài bằng độ dài đoạn thẳng BC. Ta được đoạn thẳng AD cần vẽ
– Vẽ tia đối của tia Ax ta được tia Ax’. Đường thẳng xx’ là đường thẳng song song với BC.
Bài 7:
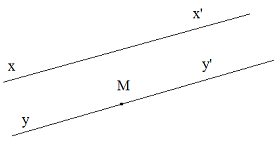
Vẽ hai đường thẳng xx’, yy’ sao cho xx’ // yy’.
Giải:
Cách vẽ:
+) Vẽ một đường thẳng tùy ý (đường thẳng xx’)
+) Vẽ một điểm M tùy ý nằm ngoài đường thẳng xx’
+) Vẽ qua M đường thẳng yy’ sao cho yy’ // xx’.
Bài 8:
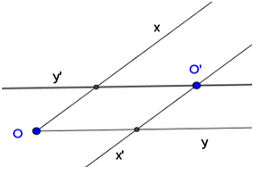
Cho góc nhọn xOy và một điểm O’. Hãy vẽ một góc nhọn x’Oy’ có O’x’ // Ox và O’y’ // Oy. Hãy đo xem hai góc xOy và x’O’y’ có bằng nhau hay không?
Giải:
Cách vẽ:
+) Từ O vẽ O’x’ // Ox
+) Từ O’ vẽ O’y’ //Oy sao cho góc x’Oy’ là góc nhọn.
Nhận xét: (widehat {xOy} = widehat {x’Oy’})
Bài 9:
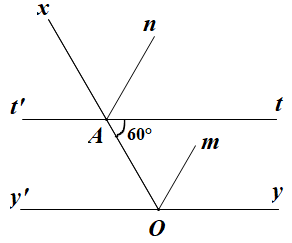
Cho góc (widehat {xOy} = {120^0}.) Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là Ox, vẽ tia At sao cho (widehat {OAt} = {60^0}.) Gọi At’ là tia đối của tia At.
a) Chứng tỏ tt’ // Oy.
b) Gọi Om, An theo thứ tự là các tia phân giác của các góc (widehat {xOy}) và (widehat {xAt}). Chứng tỏ Om // An.
Giải:
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Tải về