Bất đẳng thức Côsi là một trong những bất đẳng thức cổ điển. Tên chính xác là bất đẳng thức giữa trung bình cộng và trung bình nhân, nhiều người gọi là bất đẳng thức AM – GM (AM là viết tắt của Arithmetic mean và GM là viết tắt của Geometric mean). Do nhà toán học người Pháp Augustin – Louis Cauchy (1789 – 1857), người đã đưa ra một cách chừng mình đặc sắc nên nhiều người hay gọi là bất đẳng thức Cauchy.
Nó ứng dụng rất nhiều trong những bài Toán về bất đẳng thức và cực trị. Trong khoanh vùng phạm vi chương trình Toán trung học cơ sở, tất cả chúng ta chăm sóc đến những trường hợp riêng của bất đẳng thức Cauchy .
1. Các dạng biểu diễn của bất đẳng thức Cosi
a. Dạng tổng quát bất đẳng thức cosi
Cho x1, x2, x3, …, xn là những số thực không âm ta có :

Cho x1, x2, x3, …, xn là những số thực dương ta có :
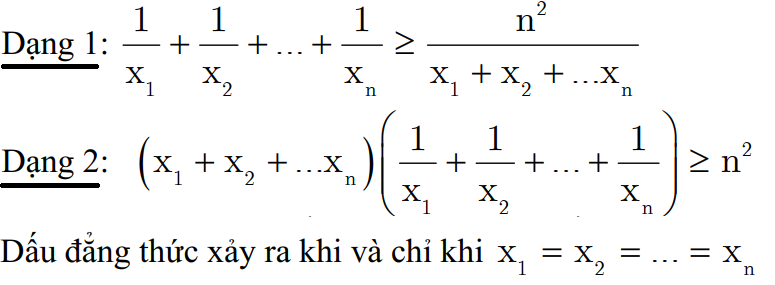
b ) Các bất đẳng thức côsi đặc biệt quan trọng

c) Một số bất đẳng thức được suy ra từ bất đẳng thức Cauchy

d) Chú ý khi sử dụng bất đẳng thức AM – GM
- Khi áp dụng bất đẳng thức cô si thì các số phải là những số không âm
- Bất đẳng thức côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích
- Điều kiện xảy ra dấu ‘=’ là các số bằng nhau
- Bất đẳng thức côsi còn có hình thức khác thường hay sử dụng
Đối với hai số :
- ${{x}^{2}}\,\,+\,{{y}^{2}}\,\,\ge \,\,2xy$.
- $\,{{x}^{2}}\,\,+\,{{y}^{2}}\,\,\ge \,\,\frac{{{(x\,+\,y)}^{2}}}{2}$
- $\,xy\le \,\,{{\left( \frac{x+y}{2} \right)}^{2}}$
Đối với ba số : USD abc \ le \ frac { { { a } ^ { 3 } } + { { b } ^ { 3 } } + { { c } ^ { 3 } } } { 3 }, \, \, abc \ le { { \ left ( \ frac { a + b + c } { 3 } \ right ) } ^ { 3 } } $
2. Các dạng bài tập
Dạng 1: Vận dụng trực tiếp bất đẳng thức côsi
Ví dụ: Cho a, b là số dương thỏa mãn a2 + b2 = 2. Chứng minh rằng ${{\left( a+b \right)}^{5}}\ge 16ab\sqrt{\left( 1+{{a}^{2}} \right)\left( 1+{{b}^{2}} \right)}$
Lời giải

Dạng 2: Kĩ thuật tách, thêm bớt, ghép cặp
- Để chứng minh BĐT ta thường phải biến đổi (nhân chia, thêm, bớt một biểu thức) để tạo biểu thức có thể giản ước được sau khi áp dụng BĐT côsi.
- Khi gặp BĐT có dạng x + y + z ≥ a + b + c (hoặc xyz ≥ abc), ta thường đi chứng minh x + y ≥ 2a (hoặc ab ≤ x2), xây dựng các BĐT tương tự rồi cộng(hoặc nhân) vế với vế ta suy ra điều phải chứng minh.
- Khi tách và áp dụng BĐT côsi ta dựa vào việc đảm bảo dấu bằng xảy ra(thường dấu bằng xảy ra khi các biến bằng nhau hoặc tại biên).
Ví dụ: Cho a, b, c là số dương thỏa mãn a + b + c = 3.
Chứng minh rằng 8( a + b )(b + c)(c + a) ≤ (3 + a)(3 + b)(3 + c)
Lời giải

Dạng 3: Kĩ thuật tham số hóa
Nhiều khi không Dự kiến được dấu bằng xảy ra ( để tách ghép cho hợp lý ) tất cả chúng ta cần đưa tham số vào rồi chọn sau sao cho dấu bằng xảy ra .
Ví dụ: Cho a, b, c là số dương thỏa mãn 2a + 4b + 3c2 = 68. Tìm giá trị nhỏ nhất của A = a2 + b2 + c3.
Phân tích

Lời giải
Áp dụng Bất đẳng thức côsi ta có

Dạng 4: Kĩ thuật bất đẳng thức côsi ngược dấu
Ví dụ: Cho a, b, c là các số thực không âm thỏa mãn a2 + b2 + c2 = 1.
Chứng minh rằng $\frac{c}{1+ab}+\frac{b}{1+ac}+\frac{a}{1+bc}\ge 1$
Lời giải

Source: https://futurelink.edu.vn
Category: Tin tổng hợp