Hình thoi nằm trong phần kiến thức ta đã được làm quen lần đầu năm lớp 4. Tới chương trình toán lớp 8, định nghĩa về hình thoi là gì được mở rộng và chuyên sâu hơn, giải đáp các thắc mắc về tính chất hình thoi, ý nghĩa của hình thoi, dấu hiệu nhận biết,…Hãy cùng nhau ôn lại kiến thức về hình thoi và tập giải các dạng toán liên quan trong bài viết sau
Định nghĩa hình thoi là gì?
Hình thoi trong tiếng Anh là Rhombus. Hình thoi là tứ giác có 4 cạnh bằng nhau.
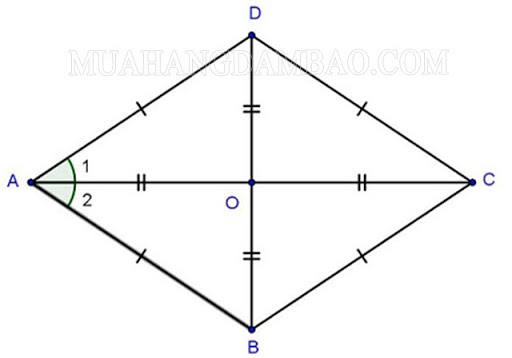
- Hình thoi cũng là hình bình hành có 2 cặp cạnh kề bằng nhau hoặc hình bình hành có 2 đường chéo vuông góc với nhau.
- Hình thoi có đầy đủ các tính chất của hình bình hành.
Lưu ý:
Nếu bạn có một hình thoi với bốn góc trong bằng nhau, bạn có một hình vuông . Hình vuông là một trường hợp đặc biệt của hình thoi, vì nó có bốn cạnh dài bằng nhau và có bốn góc vuông.

Tính chất của hình thoi là gì?
- Hình thoi có đầy đủ tính chất của hình bình hành
- Hai đường chéo vuông góc với nhau
- Hai đường chéo là đường phân giác góc của hình thoi
- Hình thoi có các góc đối bằng nhau, tổng các góc trong hình thoi bằng 360 độ
- Hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc trong hình thoi
Dấu hiệu nhận biết hình thoi
Các dấu hiệu nhận biết 1 hình là hình thoi:
- Tứ giác có 4 cạnh bằng nhau
- Hình bình hành có hai cạnh kề bằng nhau
- Hình bình hành có hai đường chéo vuông góc với nhau
- Hình bình hành có đường chéo là đường phân giác của một góc
Công thức tính diện tích, chu vi hình thoi
Cho hình thoi ABCD có độ dài cạnh là a, độ dài 2 đường chéo là d1 và d2

Công thức tính diện tích hình thoi
* Công thức tính diện tích hình thoi dựa vào 2 đường chéo
Diện tích của hình thoi được tính bằng một nửa tích (1/2) độ dài hai đường chéo.
S = ½ d1.d2
Trong đó:
- S: Diện tích hình thoi
- d1, d2: Độ dài 2 đường chéo của hình thoi
Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao

Diện tích của hình thoi được tính bằng nửa tích (1/2) chiều cao và 1 cạnh
S = ½(a+a).h = a.h
Trong đó:
- h: Chiều cao của hình thoi
- a: Cạnh đáy
* Công thức tính diện tích hình thoi dựa vào hệ thức trong tam giác (Nếu biết góc của hình thoi)
S = a2.sinA = a2.sinB = a2.sinC = a2.sinD
Trong đó:
- a: cạnh hình thoi
Công thức tính chu vi hình thoi
Chu vi của hình thoi được tính bằng độ dài một cạnh nhân với 4. Số 4 ở đây là 4 cạnh của hình thoi.
P = a.4
Trong đó:
- P: Chu vi hình thoi
- a: Một cạnh bất kỳ của hình thoi
Công Thức Tính Đường Chéo Hình Thoi
Dựa vào các công thức tính chu vi, diện tích hình thoi ở trên, ta có được công thức tính đường chéo hình thoi như sau:
* Tính đường chéo hình thoi khi biết diện tích, độ dài 1 đường chéo:
Nếu đã biết diện tích hình thoi, độ dài đường chéo (d1), dễ dàng tìm được 1 cạnh còn lại của hình thoi theo công thức sau:
d2= 2S / d1
Cách vẽ hình thoi chuẩn và nhanh chóng

Vẽ hình thoi ABCD
Có 2 cách để vẽ chính là thước kẻ – êke và thước kẻ – compa
Cách 1 : Vẽ bằng thước kẻ và êke
- Bước 1: Vẽ đoạn thẳng AC bất kì và xác định trung điểm O của đoạn thẳng AC đó.
- Bước 2: Dùng êke vẽ đoạn thẳng BD vuông góc với AC tại O và nhận O là trung điểm của BD.
- Bước 3: Nối các đỉnh A với B, B với C, C với D, D với A => được hình thoi ABCD.
Cách 2 : Vẽ bằng thước kẻ và compa
- Bước 1: Vẽ đoạn thẳng AC có độ dài bất kỳ.
- Bước 2: Dùng compa, mở rộng độ mở compa lớn hơn 12 AC. Vẽ cung tròn tâm A và tâm C sao cho hai cung tròn cắt nhau tại hai điểm, hai giao điểm này gọi là B và D.
- Bước 3: Nối các điểm A,B,C,D với nhau => được hình thoi ABCD.
Các dạng bài tập về hình thoi
Tính diện tích hình thoi biết độ dài cạnh và đường chéo
Bài 1: Cho hình thoi ABCD có độ dài AB = 10 cm, đường chéo AC = 16 cm. Tính diện tích hình thoi ABCD

Giải:
Gọi O là giao điểm hai đường chéo AC và BD, ta có OC = ½ AC = ½ . 16=8
Xét tam giác vuông BOC ta có OB2= BC2- OC2=102-82=36 ⇒OB=6(cm)
⇒ DB = 2.BO = 2.6 = 12
Suy ra diện tích hình thoi là SABCD= ½ AC.BD = ½.12.16 = 96 (cm2)
Tính diện tích hình thoi khi biết số đo góc và độ dài một cạnh kề
Ví dụ 2: Tính S hình thoi ABCD có góc A=30∘, biết AD = 4cm,
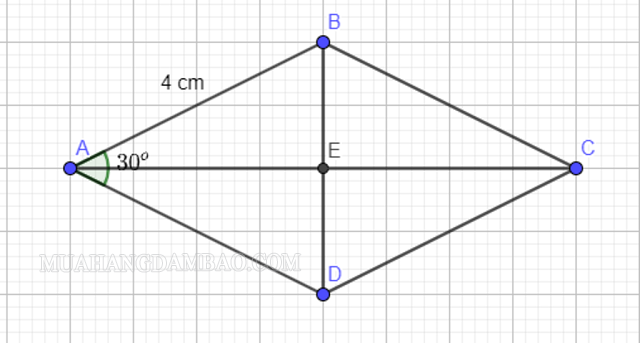
Giải:
Vì ABCD là hình thoi nên các tam giác đều là tam giác cân.
Gọi E là trung điểm 2 đường chéo. ⇒AE⊥BD và góc EAB=15∘
Áp dụng định lý Pitago trong ΔABH ta có:
BE2=AB2-AE2=42- 32⇒BE = √7(cm)
⇒DB = 2EB = 2√7(cm)
SABCD=2.SABD=2. ½ .BD.AE=2.½ 2√7.3 = 6√7 cm2
Trên đây là tổng hợp toàn bộ kiến thức liên quan đến hình thoi trong chương trình toán học lớp 4, lớp 5 và lớp 8. Ý nghĩa của hình thoi là tạo tiền đề tính toán diện tích, chu vi, các công thức liên quan tới các hình như hình vuông, hình chữ nhật, hình bình hành. Nếu bạn nắm vững kiến thức về hình thoi, khi áp dụng vào các hình học khác sẽ logic và dễ dàng hơn nhiều. Chúc các bạn có những giờ học vui vẻ và bổ ích