Bên cạnh các công thức tính diện tích, tính chu vi tam giác thì cách tính đường cao trong tam giác cân cũng là một trong những dạng bài tập thường gặp ở Toán lớp 9. Vậy đường cao trong tam giác cân là gì? Cùng GiaiNgo tìm hiểu qua bài viết sau đây.
Đường cao trong tam giác là gì?
Đường cao trong tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện. Cạnh đối diện này được gọi là đáy tương ứng với đường cao.
Mỗi tam giác có 3 đường cao. Độ dài của đường cao trong tam giác được xác định là khoảng cách giữa đỉnh và đáy.
Khi làm bài tập, các bạn cần phải xác định đúng và phân loại được các loại đường cao trong tam giác thường, vuông, cân để giải cho nhanh và chính xác.
Từ đường cao trong tam giác, bạn dễ dàng suy luận đường cao trong tam giác cân là gì rồi nhé!
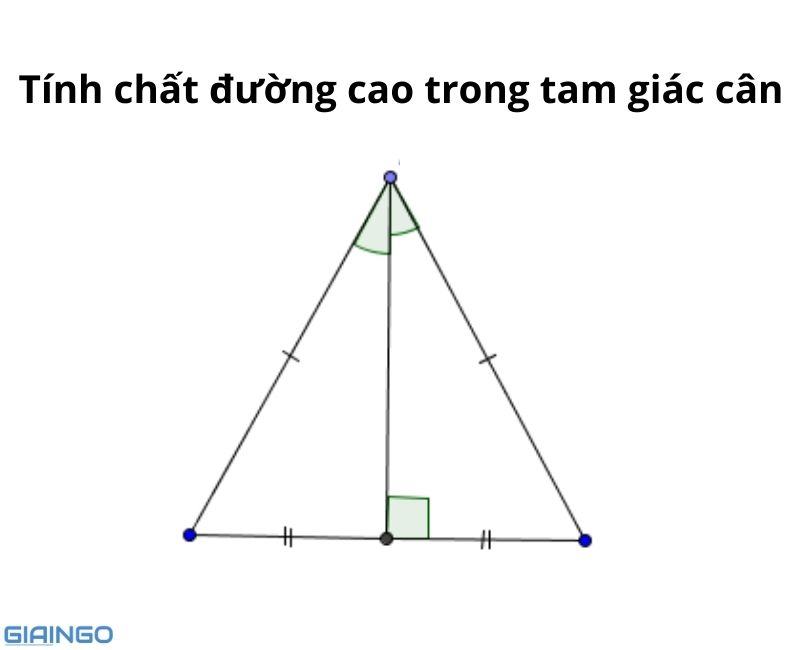
Tính chất đường cao trong tam giác cân
Tính chất đường cao trong tam giác cân gồm:
- Đường cao tam giác cân đi qua trung điểm của cạnh đáy tương ứng.
- Đường cao tam giác cân đồng thời cũng là đường phân giác của góc ở đỉnh và đường trung trực của đáy tương ứng.
- Nếu như một tam giác các có đường cao đồng thời cũng là đường trung tuyến hoặc phân giác thì tam giác đó chính là tam giác cân.
Công thức tính đường cao trong tam giác cân
Đường cao trong tam giác cân bằng bình phương độ dài một cạnh của tam giác trừ bình phương độ dài cạnh đáy chia bốn.
Công thức: h2 = a2 − b2/4
Trong đó:
- h: Chiều cao của tam giác cân
- a: Cạnh của tam giác cân
- b: Cạnh đáy tương ứng với chiều cao từ đỉnh của hình tam giác cân
Như vậy, khi biết thành phần như độ dài một cạnh của tam giác và cạnh đáy tương ứng với chiều cao từ đỉnh của là có thể tính được đường cao trong tam giác.
Cách tính đường cao trong tam giác cân
Để nắm rõ hơn về cách tính đường cao trong tam giác cân, mời mọi người cùng theo dõi ví dụ sau.
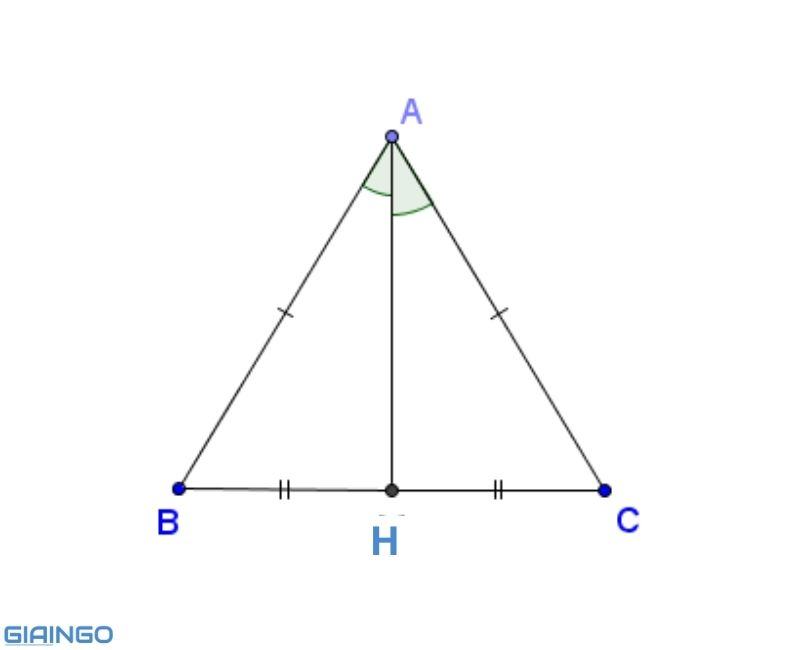
Cho tam giác ABC cân tại A, đường cao AH vuông góc tại H như sau. Tính đường cao AH.
Hướng dẫn
Vì tam giác ABC cân tại A, đường cao AH đồng thời là đường trung tuyến nên:
Áp dụng định lý Pythagore trong tam giác vuông ABH vuông tại H ta có:
AH2 + BH2 = AB2
=> AH2 = AB2 − BH2
Xem thêm:
- Tính chất đường phân giác trong tam giác? Lý thuyết & bài tập
- Cách chứng minh tam giác cân? Dấu hiệu, tính chất, công thức
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
Bài tập về tính đường cao trong tam giác cân
Để hiểu hơn về nội dung đường cao trong tam giác cân, chúng ta cùng giải các bài tập về tính đường cao trong tam giác cân nhé.
Bài tập 1
Cho tam giác cân ABC cân tại A có độ dài hai cạnh AB = AC = 4cm, BC = 14m. Tính chiều dài đường cao trong tam giác cân ABC.
Trả lời
Kẻ đường cao AH vuông góc với BC tại H.
Vì đường cao tam giác cân đi qua trung điểm của cạnh đáy nên:
BH = HC = BC/2 = 14/2 = 7 cm
Áp dụng công thức bên trên ta có:
AH2 + BH2 = AB2
=> AH2 = AB2 − BH2 = 16 – 7 = 9
Độ dài AH = √9 = 3 cm.
Bài tập 2
Tính chiều dài đường cao trong tam giác cân có độ dài 2 cạnh bằng nhau là 2cm và độ dài cạnh còn lại là 3.
Trả lời
Áp dụng công thức trên ta có :
Độ dài đường cao trong tam giác cân h = √[ a2 – (b/2)2] = √(4 – (1.5)2) = 1.32 (cm)
Bài tập 3
Cho tam giác DEF cân tại A có DE + DF = 22cm, EF = 10. Kẻ DI vuông góc với EF tại I. Tính độ dài đường cao DI.
Trả lời
Vì tam giác DEF cân tại D nên DE = DF = 22/2 = 11 cm
Vì đường cao tam giác cân đi qua trung điểm của cạnh đáy nên
EI = IF = EF/2 = 10/2 = 5 cm
Áp dụng công thức bên trên ta có:
DI2 + EI2 = DE2
=> DI2 = DE2 − EI2 = 121 – 25 = 96
Độ dài DI = √96 = 4√6 cm.

Vừa rồi GiaiNgo đã chia sẻ cho bạn những thông tin về đường cao trong tam giác cân. Hy vọng qua bài viết trên bạn đã làm được chính xác dạng Toán này. Đừng quên theo dõi GiaiNgo để biết thêm nhiều kiến thức bổ ích trong học tập nhé!