Giải Toán 12 bài: Nguyên hàm
Trả lời câu hỏi SGK Toán Giải tích 12 Bài 1 (Chương 3):
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 93 (1):
Tìm hàm số F ( x ) sao cho F ’ ( x ) = f ( x ) nếu :
a ) f ( x ) = 3×2 với x ∈ ( – ∞ ; + ∞ ) ;
b) f(x) = 1/(cosx)2 với x ∈ ((-π)/2; π/2).
Bạn đang đọc: Toán 12: Nguyên Hàm – Giải bài tập SGK (Hay nhất)
Lời giải:
F ( x ) = x3 vì ( x3 ) ‘ = 3×2
F ( x ) = tanx vì ( tanx ) ‘ = 1 / ( cos x ) 2 .
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 93 (2):
Hãy tìm thêm những nguyên hàm khác của những hàm số nêu trong Ví dụ 1 .
Lời giải:
( x ) = x2 + 2 do ( F ( x ) ) ‘ = ( x2 + 2 ) ’ = 2 x + 0 = 2 x. Tổng quát F ( x ) = x2 + c với c là số thực .
F ( x ) = lnx + 100, do ( F ( x ) ) ’ = 1 / x, x ∈ ( 0, + ∞ ). Tổng quát F ( x ) = lnx + c, x ∈ ( 0, + ∞ ) và với c là số thực .
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 93 (3):
Hãy chứng minh Định lý 1 .
Lời giải:
Vì F ( x ) là nguyên hàm của f ( x ) trên K nên ( F ( x ) ) ‘ = f ( x ). Vì C là hằng số nên ( C ) ’ = 0 .
Ta có :
( G ( x ) ) ‘ = ( F ( x ) + C ) ‘ = ( F ( x ) ) ‘ + ( C ) ‘ = f ( x ) + 0 = f ( x )
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 95:
Hãy chứng tỏ Tính chất 3 .
Lời giải:
Ta có [ ∫ f ( x ) ± ∫ g ( x ) ] ‘ = [ ∫ f ( x ) ] ‘ ± [ ∫ g ( x ) ] ‘ = f ( x ) ± g ( x ) .
Vậy ∫ f ( x ) ± ∫ g ( x ) = ∫ [ f ( x ) ± g ( x ) ] .
Vậy G ( x ) là một nguyên hàm của f ( x ) .
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 96:
Lập bảng theo mẫu dưới đây rồi dùng bảng đạo hàm trang 77 và trong SGK Đại số và Giải tích 11 để điền vào những hàm số thích hợp vào cột bên phải .
Lời giải:
| f’(x) | f(x) + C |
| 0 | C |
| αxα -1 | xα + C |
| 1/x (x ≠ 0) | ln(x) + C nếu x > 0, ln(-x) + C nếu x < 0. |
| ex | ex + C |
| axlna (a > 1, a ≠ 0) | ax + C |
| Cosx | sinx + C |
| – sinx | cosx + C |
| 1/(cosx)2 | tanx + C |
| (-1)/(sinx)2 | cotx + C |
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 98:
a ) Cho ∫ ( x – 1 ) 10 dx. Đặt u = x – 1, hãy viết ( x – 1 ) 10 dx theo u và du .
b ) ∫Đặt x = et, hãy viếttheo t và dt .a ) Ta có ( x – 1 ) 10 dx = u10 du ( do du = d ( x – 1 ) = dx .
b ) Ta có dx = d ( et ) = et dt, do đó
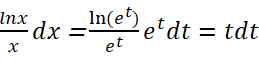
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 99:
Ta có ( xcosx ) ’ = cosx – xsinx hay – xsinx = ( xcosx ) ’ – cosx .
Hãy tính ∫ ( xcosx ) ’ dx và ∫ cosxdx. Từ đó tính ∫ xsinxdx .
Lời giải:
Ta có ∫ ( xcosx ) ’ dx = ( xcosx ) và ∫ cosxdx = sinx. Từ đó
∫ xsinxdx = – ∫ [ ( xcosx ) ’ – cosx ] dx = – ∫ ( xcosx ) ’ dx + ∫ cosxdx = – xcosx + sinx + C .
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 100:
Cho P. ( x ) là đa thức của x. Từ Ví dụ 9, hãy lập bảng theo mẫu dưới đây rồi điền u và dv thích hợp vào chỗ trống theo chiêu thức nguyên phân hàm từng phần .
| ∫ P(x)ex dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | ||
| exdx |
Lời giải:
| ∫ P(x)ex dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | P(x) | P(x)lnx |
| exdx | cosxdx | dx |
Giải bài tập SGK Toán Giải tích 12 Bài 1 (Chương 3):
Bài 1 (trang 100 SGK Giải tích 12):
Trong những cặp hàm số dưới đây, hàm số nào là nguyên hàm của hàm số còn lại ?
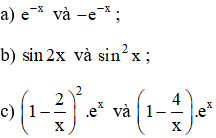
Lời giải:
a ) Ta có : ( – e-x ) ‘ = – e-x. ( – x ) ‘ = e-x
⇒ – e-x là một nguyên hàm của hàm số e-x
Lại có : ( e-x ) ’ = e-x. ( – x ) ’ = – e-x
Suy ra, e-x là một nguyên hàm của hàm số – e-x
Vậyb ) ( sin2x ) ‘ = 2.sinx. ( sinx ) ‘ = 2.sinx.cosx = sin2x
⇒ sin2x là một nguyên hàm của hàm số .
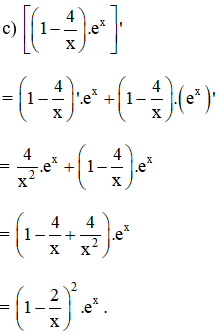
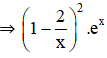 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 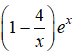
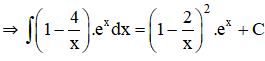
Bài 2 (trang 100 SGK Giải tích 12):
Tìm hiểu nguyên hàm của những hàm số sau :
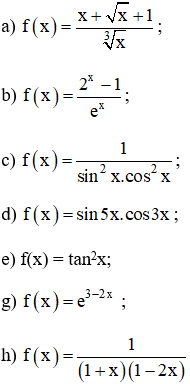
Lời giải:
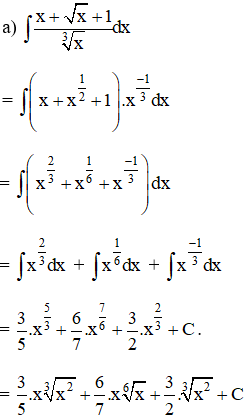
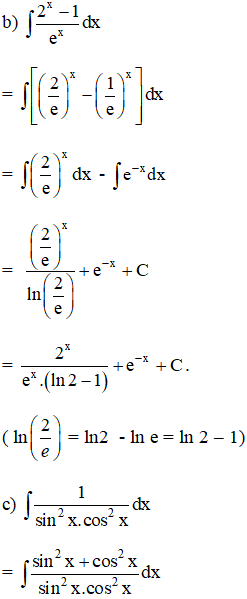
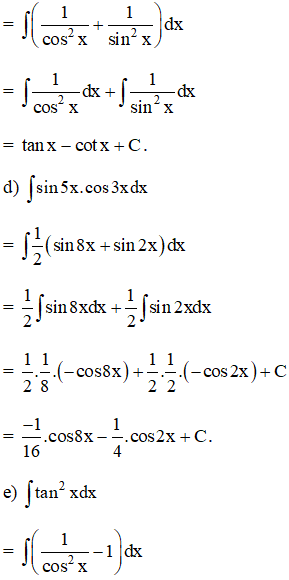
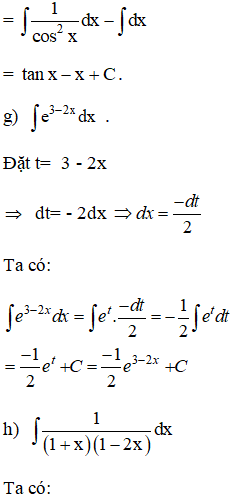
.png)
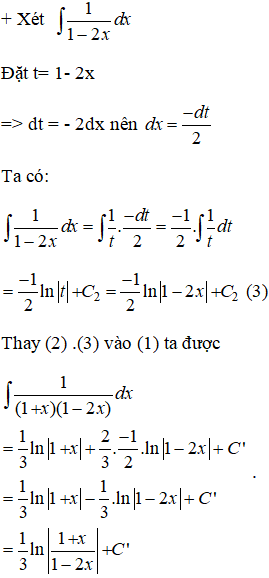
Bài 3 (trang 101 SGK Giải tích 12):
Sử dụng chiêu thức đổi biến, hãy tính :
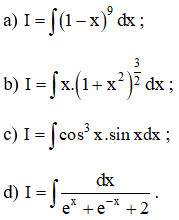
Lời giải:
a ) Đặt u = 1 – x ⇒ u ’ ( x ) = – 1 ⇒ du = – dx hay dx = – du
Thay u = 1 – x vào tác dụng ta được :
b ) Đặt u = 1 + x2 ⇒ u ‘ = 2 x ⇒ du = 2x.dx
Thay lại u = 1 + x2 vào hiệu quả ta được :
c ) Đặt u = cosx ⇒ u ‘ = – sinx ⇒ du = – sinx.dx
Thay lại u = cos x vào hiệu quả ta được :
d ) Ta có :
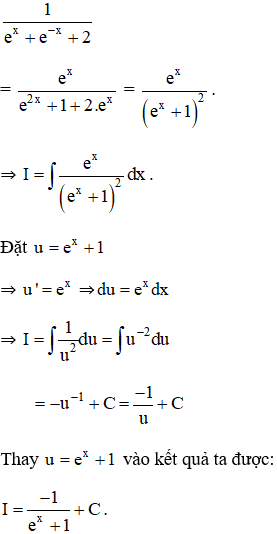
Bài 4 (trang 101 SGK Giải tích 12):
Sử dụng giải pháp tính nguyên hàm từng phần, hãy tính :
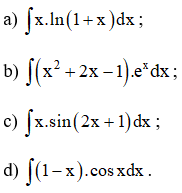
Lời giải:
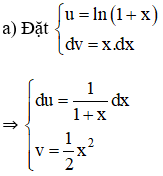
Theo công thức nguyên hàm từng phần ta có :
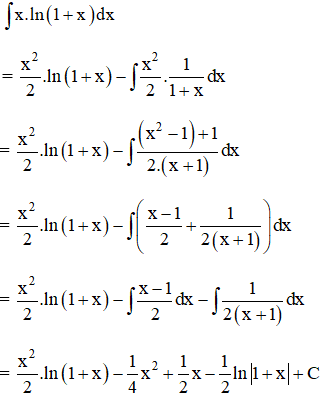
b ) Đặt
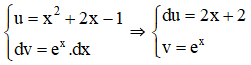
Theo công thức nguyên hàm từng phần ta có :
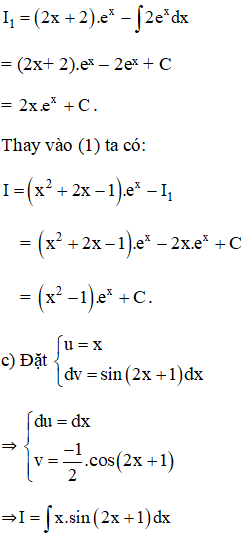
Theo công thức nguyên hàm từng phần ta có :
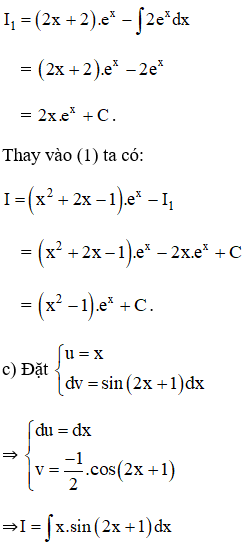
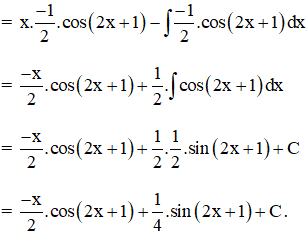
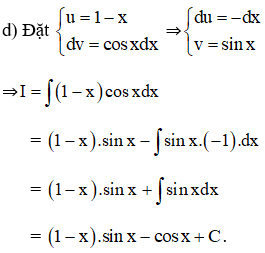
Ngoài ra những em học viên và thầy cô hoàn toàn có thể tìm hiểu thêm thêm nhiều tài liệu hữu dụng rất đầy đủ những môn được update liên tục tại chuyên trang của chúng tôi .
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập nguyên hàm lớp 12 file Word, pdf hoàn toàn miễn phí!
Source: https://futurelink.edu.vn
Category: Tin tổng hợp