Giải bài 16, 17, 18 trang 22 SGK Giải tích 12 Nâng cao

Bởi

Bài 16 trang 22 SGK Đại số và Giải tích 12 Nâng cao

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(f\left( x \right) = {\sin ^4}x + {\cos ^4}x\)

Giải

TXĐ: \(D=\mathbb R\)

\(\eqalign{
& f\left( x \right) = {\left( {{{\sin }^2}x} \right)^2} + {\left( {{{\cos }^2}x} \right)^2} + 2{\sin ^2}x{\cos ^2}x \cr&\,\,\,\,\,\,\,\,\,\,\,\;\;\;\;- 2{\sin ^2}x{\cos ^2}x \cr 
& \,\,\,\,\,\,\,\,\,\,\,\;\; = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} – 2{\sin ^2}x{\cos ^2}x \cr&\,\,\,\,\,\,\,\,\,\,\,\;\;= 1 – {1 \over 2}{\sin ^2}2x \cr} \)

Vì \ ( 0 \ le { \ sin ^ 2 } 2 x \ le 1 \ ) nên : \ ( \, \, f \ left ( x \ right ) \ le 1 \ ) với mọi \ ( x \ in { \ mathbb { R } }, f \ left ( 0 \ right ) = 1 \ ). Vậy \ ( \ mathop { \ max f \ left ( x \ right ) } \ limits_ { x \ in { \ mathbb { R } } } = 1 \ )
\ ( * \, \, \, f \ left ( x \ right ) \ ge { 1 \ over 2 } \ ) với mọi \ ( x \ in { \ mathbb { R } }, f \ left ( { { \ pi \ over 4 } } \ right ) = 1 – { 1 \ over 2 } = { 1 \ over 2 } \ )
Vậy \ ( \ mathop { \ min f \ left ( x \ right ) } \ limits_ { x \ in { \ mathbb { R } } } = { 1 \ over 2 } \ ) .

Bài 17 trang 22 SGK Đại số và Giải tích 12 Nâng cao

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) \(f\left( x \right) = {x^2} + 2x – 5\) trên đoạn \(\left[ { – 2;3} \right]\);

b) \(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x – 4\) trên đoạn \(\left[ { – 4;0} \right]\);

c) \(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\);

d) \(f\left( x \right) =  – {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\);

e) \(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\);

f) \(f\left( x \right) = x – {1 \over x}\) trên đoạn \(\left( {0;2} \right]\);

Giải

a ) \ ( D = \ left [ { – 2 ; 3 } \ right ] ; f ‘ \ left ( x \ right ) = 2 x + 2 ; f ‘ \ left ( x \ right ) = 0 \ )
\ ( \ Leftrightarrow x = – 1 \ in \ left [ { – 2 ; 3 } \ right ] \ )
Ta có : \ ( f \ left ( { – 2 } \ right ) = – 5 ; f \ left ( { – 1 } \ right ) = – 6 ; f \ left ( 3 \ right ) = 10 \ ) .
Vậy : \ ( \ mathop { \ min \, f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { – 2 ; 3 } \ right ] } = – 6 ; \, \, \, \, \, \, \ mathop { \ max \, f \ left ( x \ right ) = 10 } \ limits_ { x \ in \ left [ { – 2 ; 3 } \ right ] } \ ) .
b )
\ ( D = \ left [ { – 4 ; 0 } \ right ] ; \, f ‘ \ left ( x \ right ) = { x ^ 2 } + 4 x + 3 ; f ‘ \ left ( x \ right ) = 0 \ )

\(\Leftrightarrow \left[ \matrix{
x = – 1 \in \left[ { – 4;0} \right] \hfill \cr 
x = – 3 \in \left[ { – 4;0} \right] \hfill \cr} \right.\)

Ta có : \ ( f \ left ( { – 4 } \ right ) = – { { 16 } \ over 3 } ; f \ left ( { – 1 } \ right ) = – { { 16 } \ over 3 } ; \ )
\ ( f \ left ( { – 3 } \ right ) = – 4 ; f \ left ( 0 \ right ) = – 4 \ )
Vậy \ ( \ mathop { \ min \, f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { – 4 ; 0 } \ right ] } = – { { 16 } \ over 3 } ; \, \, \ mathop { \ max \, f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { – 4 ; 0 } \ right ] } = – 4 \ ) .
c ) \ ( D = \ left ( { 0 ; + \ infty } \ right ) ; f ‘ \ left ( x \ right ) = 1 – { 1 \ over { { x ^ 2 } } } = { { { x ^ 2 } – 1 } \ over { { x ^ 2 } } } \ ) với mọi \ ( x \ ne 0, f ‘ \ left ( x \ right ) = 0 \ Leftrightarrow x = \ pm 1 \ )
\ ( x = 1 \ in \ left \ { { 0 ; + \ infty } \ right. ) \ )
\ ( x = – 1 \ not \ in \ left \ { { 0 ; + \ infty } \ right. ) \ )

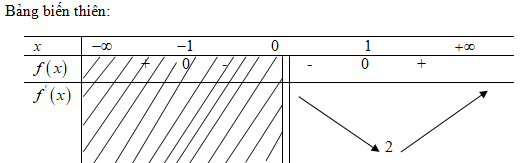
\ ( \ mathop { \ min \, \, f \ left ( x \ right ) = f \ left ( 1 \ right ) } \ limits_ { x \ in \ left ( { 0 ; + \ infty } \ right ) } = 2 \ ). Hàm số không đạt giá trị lớn nhất trên khoảng chừng \ ( \ left ( { 0 ; + \ infty } \ right ) \ ) .

d) \(D = \left[ {2;4} \right];f’\left( x \right) =  – 2x + 2;f’\left( x \right) = 0 \)

\ ( \ Leftrightarrow x = 1 \ notin \ left [ { 2 ; 4 } \ right ] \ )
Ta có : \ ( f \ left ( 2 \ right ) = 4 ; f \ left ( 4 \ right ) = – 4 \ )
Vậy \ ( \ mathop { \ min \, f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { 2 ; 4 } \ right ] } = – 4 ; \, \ ) \ ( \ mathop { \ max f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { 2 ; 4 } \ right ] } = 4 \ ) .
e )
\ ( D = \ left [ { 0 ; 1 } \ right ] ; f ‘ \ left ( x \ right ) = { { 2 { x ^ 2 } + 8 x + 6 } \ over { { { \ left ( { x + 2 } \ right ) } ^ 2 } } } ; f ‘ \ left ( x \ right ) = 0 \ )

\(\Leftrightarrow \left[ \matrix{
x = – 1 \notin \left[ {0;1} \right] \hfill \cr 
x = – 3 \notin \left[ {0;1} \right] \hfill \cr} \right.\)

Ta có : \ ( f \ left ( 0 \ right ) = 2 ; f \ left ( 1 \ right ) = { { 11 } \ over 3 } \ )
Vậy \ ( \ mathop { \ min \, f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { 0 ; 1 } \ right ] } = 2 ; \ ) \ ( \ mathop { \ max f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { 0 ; 1 } \ right ] } = { { 11 } \ over 3 } \ )
f ) \ ( D = \ left ( { 0 ; 2 } \ right ] ; f ‘ \ left ( x \ right ) = 1 + { 1 \ over { { x ^ 2 } } } > 0 \ ) với mọi \ ( x \ in \ left ( { 0 ; 2 } \ right ] ; f \ left ( 2 \ right ) = { 3 \ over 2 } \ )

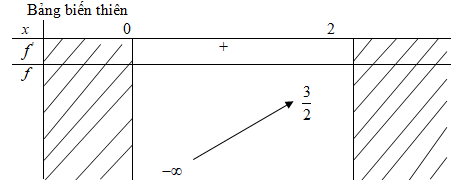
\ ( \ mathop { \, \ max f \ left ( x \ right ) } \ limits_ { x \ in \ left [ { 0 ; 2 } \ right ] } = { 3 \ over 2 } \ ). Hàm số không đạt giá trị nhỏ nhất trên \ ( \ left ( { 0 ; 2 } \ right ] \ ) .

Bài 18 trang 22 SGK Đại số và Giải tích 12 Nâng cao

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) \(y = 2{\sin ^2}x + 2\sin x – 1\)

b) \(y = {\cos ^2}2x – \sin x\cos x + 4\)

Giải

a ) Đặt \ ( t = \ sin x, – 1 \ le t \ le 1 \ )
\ ( y = f \ left ( t \ right ) = 2 { t ^ 2 } + 2 t – 1 \ )
Ta tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \ ( y = f \ left ( t \ right ) \ ) trên đoạn \ ( \ left [ { – 1 ; 1 } \ right ] \ ). Đó cũng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên \ ( \ mathbb R \ ) .
\ ( f ‘ \ left ( t \ right ) = 4 t + 2 ; f ‘ \ left ( t \ right ) = 0 \ Leftrightarrow t = – { 1 \ over 2 } \ )
Ta có : \ ( f \ left ( { – 1 } \ right ) = – 1 ; f \ left ( { – { 1 \ over 2 } } \ right ) = – { 3 \ over 2 } ; f \ left ( 1 \ right ) = 3 \ )
\ ( \ mathop { \ min \, \, f \ left ( t \ right ) } \ limits_ { t \ in \ left [ { – 1 ; 1 } \ right ] } = – { 3 \ over 2 } ; \, \, \, \, \, \, \ mathop { \ max \, \, f \ left ( t \ right ) } \ limits_ { t \ in \ left [ { – 1 ; 1 } \ right ] } = 3 \ )
Vậy \ ( \ mathop { \ min \, \, y } \ limits_ { x \ in { \ mathbb { R } } } = – { 3 \ over 2 } ; \, \, \, \, \, \, \ mathop { \ max \, \, y } \ limits_ { x \ in { \ mathbb { R } } } = 3 \ ) .
b ) Ta có : \ ( y = 1 – { \ sin ^ 2 } 2 x – { 1 \ over 2 } \ sin 2 x + 4 \ )
\ ( = – { \ sin ^ 2 } 2 x – { 1 \ over 2 } \ sin 2 x + 5 \ )
Đặt \ ( t = \ sin 2 x, – 1 \ le t \ le 1 \ )
\ ( y = f \ left ( t \ right ) = – { t ^ 2 } – { 1 \ over 2 } t + 5 ; f ‘ \ left ( t \ right ) = – 2 t – { 1 \ over 2 } ; \ )
\ ( f ‘ \ left ( t \ right ) = 0 \ Leftrightarrow t = – { 1 \ over 4 } \ in \ left [ { – 1 ; 1 } \ right ] \ )

Ta có: \(f\left( { – 1} \right) = {9 \over 2};f\left( { – {1 \over 4}} \right) = {{81} \over {16}};f\left( 1 \right) = {7 \over 2}\)

\ ( \ mathop { \ min \, \, f \ left ( t \ right ) } \ limits_ { t \ in \ left [ { – 1 ; 1 } \ right ] } = { 7 \ over 2 } ; \, \, \, \, \, \ mathop { \ max \, \, f \ left ( t \ right ) } \ limits_ { t \ in \ left [ { – 1 ; 1 } \ right ] } = { { 81 } \ over { 16 } } \ )
Vậy \ ( \ mathop { \ min \, \, y } \ limits_ { x \ in { \ mathbb { R } } } = { 7 \ over 2 } ; \, \, \, \, \, \ mathop { \ max \, \, y } \ limits_ { x \ in { \ mathbb { R } } } = { { 81 } \ over { 16 } } \ ) .

Giaibaitap.me