Hình trụ tròn là hình có hai mặt đáy là hai hình tròn song song với nhau và bằng nhau. Ta có thể thấy rất nhiều hình trụ được sử dụng trong thực tế có thể kể đến như: lon sữa bò, cốc uống nước, lọ hoa, thùng đựng nước,… Hình trụ được sử dụng khá phổ biến trong thực tế do đó cách tính thể tích hình trụ cũng được áp dụng rất nhiều trong thực tế. Để có thể tính được thể tích hình trụ thì bài viết dưới đây là một trong những bài viết mà các em không nên bỏ qua.
Để tính thể tích khối trụ, ta lấy chiều cao nhân với bình phương độ dài của bán kính hình tròn ở mặt đáy hình trụ và số pi.
V = π. r2. h
Trong đó:
V là thể tích khối trụ có đơn vị là mét khối (m3)
r là bán kính hình tròn ở mặt đáy khối trụ
h là chiều cao của khối trụ
π là hằng số pi ( π = 3, 14)
Bài 1: Tính thể tích của khối trụ biết khoảng cách giữa hai tâm đáy là a (cm) và đường kính của đáy là b(cm)
Bài 2: Cho hình chữ nhật ABCD có AC = 10cm, AB=6cm. Cho đường gấp khúc ABCD quay quanh AD ta được 1 hình trụ. Tính thể tích khối trụ được giới hạn bởi hình trụ trên.
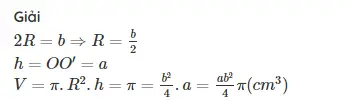
Bài 3: Cho một hình trụ bất kỳ có bán kính mặt đáy r = 4 cm , trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm . Hỏi thể tích của hình trụ này bằng bao nhiêu ?
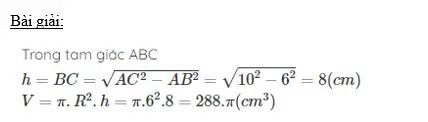
Bài giải:
Bán kính mặt đáy hình trụ r = 4cm, chiều cao hình trụ h = 8cm. Áp dụng công thức tính thể tích hình trụ ta được kết quả như sau:
V = π x r2 x h = π x 42 x 8 = ~ 402 cm3
Bài 4: Cho hình trụ có đáy là hai hình tròn tâm O và O’, bán kính đáy bằng 2. Trên đường tròn đáy tâm O lấy dây cung AB=2. Biết rằng thể tích khối tứ diện OO’AB là 8. Tính thể tích khối trụ.
Giải:
Tam giác OAB có OA = OB = AB = 2
SOAB =
Tam giác OAB có OA = OB và OO’ vuông góc với (OAB)
Suy ra OO’
Vậy thể tích hình trụ là:
Bài 5: Cho hình trụ có bán kính đáy x, chiều cao y, diện tích toàn phần bằng . Với giá trị x nào thì hình trụ tồn tại ? Tính thể tích V của khối trụ theo x và tìm giá trị lớn nhất của V
Đáp án: hình trụ tồn tại khi 0 < x < 1
Bài 6: Bên trong hình trụ có một hình vuông ABCD cạnh a nối tiếp mà A, B thuộc đường tròn đáy thứ nhất và C, D thuộc đường tròn đáy thứ 2 của hình trụ, mặt phẳng hình vuông tạo với đáy hình trụ một góc 450. Tính thể tích khối trụ
Bài 7: Cho một hình lăng trụ đứng ABCA1B1C1 có ABC là tam giác vuông. AB = AC = a;
AA1 = a . M là trung điểm AA1 . Tính thể tích hình lăng trụ MA1BC1
Bài 8: Cho hình lăng trụ ABCA’B’C’ có đáy là tam giác đều cạnh a, cạnh bên AA’ = b. Tam giác BAC’ và tam giác B’AC là các tam giác vuông tại A
a) Chứng minh rằng: Nếu H là trọng tâm của tam giác A’B’C’ thì AH vuông góc với (A’B’C’)
b) Tính VABCA’B’C’
Đáp án
Bài 9: Cho hình trụ có đáy là đường tròn tâm O và O’ tứ giác ABCD là hình vuông nội tiếp trong đường tròn tâm O, AA’, BB’ là các đường sinh của khối trụ. Biết góc của mặt phẳng (A’B’CD) và đáy hình trụ bằng 600 . Tính thể tích khối trụ
Đáp số:
Bài 10: Một hình trụ có diện tích toàn phần . Xác định các kích thước của khối trụ để thể tích của khối trụ này lớn nhất
Đáp số: Vmax khi R = 1, h = 2
Bài 11: Cho hình trụ có 2 đáy là 2 đường tròn tâm O và O’, bán kính đáy bằng r, chiều cao bằng h. Hai điểm A, B lần lượt thay đổi trên 2 đường tròn đáy sao cho độ dài AB = d không đổi (d>h).
a) Tính thể tích của tứ diện OO’AB theo r, h, d.
b) Chứng minh rằng: khoảng cách giữa 2 đường thẳng AB và OO’ không đổi
Bài 12: Cho hình lăng trụ ABCA’B’C’ có độ dài cạnh bên bằng 2a, tam giác ABC là tam giác vuông tại A, AB = a, Hình chiếu vuông góc của A’ trên (ABC) là trung điểm BC. Tính VA’ABC theo a ?
Đáp án: VA’ABC = a3 / 2