Bài toán tìm diện tích lục giác là dạng bài thường gặp trong các bài tập tính toán chu vi, diện tích hình học, tuy nhiên có rất nhiều người còn chưa biết hoặc chưa nhớ ra cách tính diện tích của hình lục giác. Nếu bạn còn đang băn khoăn về phần kiến thức đó, vậy bạn có thể củng cố lại cũng như bổ sung thêm kiến thức cho mình về cách làm bài tập này ngay sau đây.
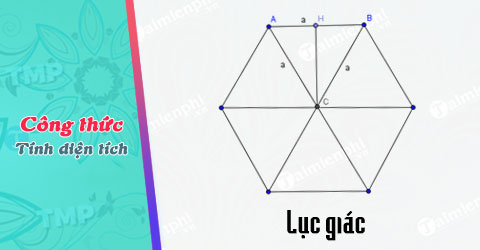
Cách tính diện tích lục giác
Công thức tính diện tích lục giác
1. Cách tính diện tích của lục giác thường
– Muốn tính diện tích của hình lục giác thường, ta có thể chia hình lục giác thành 4 hình tam giác, tính tổng diện tích của các tam giác đó là tìm ra diện tích của hình lục giác.
2. Cách tính diện tích của lục giác đều
Để tính được diện tích của hình lục giác đều, ta sử dụng công thức như sau:
S = 3√3 a2 : 2
Trong đó:
S là kí hiệu diện tícha là độ dài cạnh của lục giác
Các dạng bài tìm diện tích của lục giác
Dạng 1 : Tính diện tích lục giác đều khi biết độ dài một cạnh
Hình lục giác đều gồm sáu tam giác đều, bởi vậy diện tích của lục giác đều sẽ có liên quan đến cách tính diện tích tam giác đều.
– Trường hợp 1: Đã biết độ dài một cạnh
=> Ta chỉ cần thay số vào công thức tính diện tích như trên.
– Trường hợp 2: Xác định độ dài một cạnh qua những yếu tố khác
Khi đã biết chu vi lục giác (P):
Áp dụng công thức: P = 6a => a = P : 6
+ Sau khi đã tìm được độ dài cạnh của hình lục giác, ta chỉ cần thay thế vào công thức tính diện tích là có thể tìm ra đáp án.
Dạng 2 : Tính diện tích lục giác khi biết đường trung đoạn, biết chu vi
Áp dụng công thức tính diện tích của lục giác đều khi biết trung đoạn:
S = 1⁄2 x chu vi x trung đoạn
– Trung đoạn: Là đoạn thẳng vuông góc kẻ từ tâm của lục giác đều đến một cạnh của nó.
Dạng 3 : Tính diện tích của lục giác không đều khi biết tọa độ các đỉnh
Đối với dạng bài tập này, các bạn có thể giải như sau:
– Ghi tọa độ của tất cả các đỉnh lục giác bao gồm tọa độ x và tọa độ y- Nhân tọa độ x của đỉnh trước với tọa độ y của đỉnh tiếp theo, rồi cộng các kết quả lại với nhau. Gọi là nhóm kết quả (1).- Nhân tọa độ y của đỉnh trước với tọa độ x của đỉnh tiếp theo, cộng các kết quả lại. Gọi là nhóm kết quả (2).- Lấy kết quả của nhóm (1) trừ đi kết quả của nhóm (2)- Lấy giá trị tuyệt đối của kết quả này, lưu ý độ dài diện tích luôn là số dương.- Tiếp tục chia kết quả trên cho 2 => ta được diện tích hình lục giác cần tính.
Việc nắm được công thức và cách tính diện tích lục giác hay công thức tính chu vi lục giác là rất cần thiết và quan trọng trong quá trình giải các bài tập hình học, bởi vậy chúng tôi hi vọng với những kiến thức chia sẻ trên đây sẽ hữu ích đối với độc giả, đặc biệt là các em học sinh trong quá trình làm bài tập ở nhà cũng như khi học trên lớp. Nếu các em sưu tầm được công thức hay cách giải nào thú vị, các em có thể chia sẻ cùng chúng tôi để kiến thức Toán học trở nên phong phú hơn.