Việc lựa chọn đúng công thức tính diện tích tam giác vuông, thường, cân, vuông cân hay tam giác đều không chỉ giúp chúng ta giải một bài toán nhanh ra mà còn giúp bạn có một đáp số chuẩn nữa . Những công thức tính diện tích tam giác hầu hết chúng ta đều được học hết từ cấp 2 nhưng cũng có người lâu không sử dụng lại quên cho nên hôm nay Legoland xin tổng hợp lại công thức tính diện tích tam giác thường, vuông, cân và đều cho mọi người.
Có mấy loại tam giác ?
Đối với tam giác thì chúng ta sẽ có các loại tam giác sau :
- Tam giác vuông
- Tam giác cân
- Tam giác vuông cân
- Tam giác thường
- Tam giác đều
Xem ngay bài giảng về diện tích của các loại tam giác hay và chi tiết nhé
Các điều kiện để tính được diện tích tam giác :
Thực ra không phải chỉ có 1 kích thước 1 cạnh là chúng ta có thể tính được diện tích của tam giác đó mà nó còn phụ thuộc vào nhiều yếu tố khác nữa . Nhưng để mà tính được diện tích thì chúng ta cần phải có tối thiểu các thông số như số đo góc, kích thước cạnh hoặc chu vi …
Tham khảo thêm cách tính diện tích các hình khác :
- Công thức tính diện tích hình bình hành, chu vi kèm 5 ví dụ
- Cách tính thể tích & diện tích hình chóp tứ giác đều chuẩn
- Công thức tính diện tích hình trụ, hình nón chuẩn
- Công thức tính thể tích khối nón và thể tích hình trụ chuẩn
Công thức tính diện tích tam giác vuông, cân, đều, thường
Công thức tính diện tích tam giác thường
Định nghĩa
Tam giác thường là tam giác có độ dài các cạnh khác nhau, số đo góc trong khác nhau.
Cách tính chu vi tam giác thường
Hình tam giác thường có chu vi bằng tổng độ dài 3 cạnh. Chính vì thế chúng ta có thể áp dụng công thức sau :
P = a + b + c
Trong đó:
- P: Chu vi tam giác.
- a, b, c: là kích thước 3 cạnh của tam giác thường
Ví dụ : Cho tam giác có 3 có chiều dài 3 cạnh lần lượt là : AB = 5cm , BC = 6cm , AC = 4cm . Tính chu vi tam giác ?
Áp dụng công thức trên thì chúng ta có thể thực hiện tính chu vi tam giác : P = 5 + 6 + 4 = 15cm
=> Chu vi tam giác là : 15cm
Công thức tính diện tích tam giác khi biết chiều cao
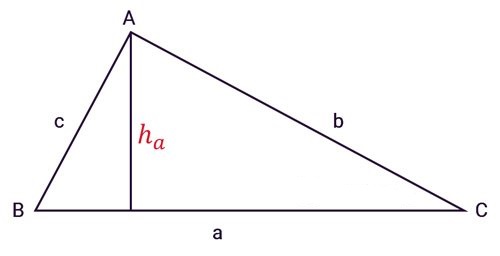
Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.
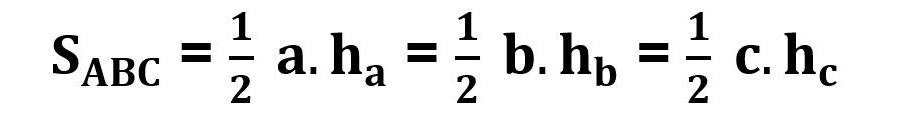
Trong đó:
- a, b, c: Lần lượt là độ dài các cạnh của tam giác.
- ha, hb, hc: Lần lượt là chiều cao được nối từ đỉnh A,B, C.
Ví dụ : Cho 1 tam giác ABC với các cạnh lần lượt là : AB = 2cm và chiều cao nối từ đỉnh A vuông góc với cạnh BC là 6cm . Tính diện tích tam giác ABC ?
Áp dụng công thức trên thì chúng ta sẽ tính được diện tích tam giác như sau :
Diện tích tam giác ABC = 1/2 * (2* 6) = 6cm2
Công thức tính diện tích tam giác thường khi biết 1 góc nào đó

Công thức tính diện tích tam giác ABC sẽ bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
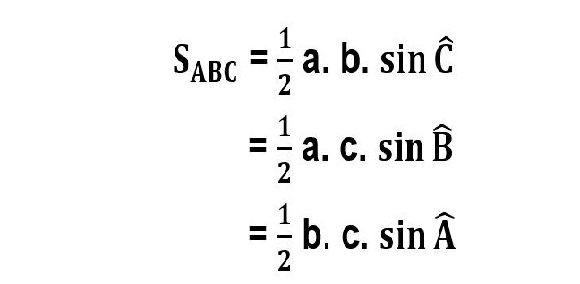
Ví dụ : Tính diện tích tam giác ABC trong đó có cạnh AB = 3cm , Cạnh BC = 4cm , góc ABC = 30 độ
Áp dụng công thức thì chúng ta sẽ tính được điện tích tam giác ABC = 1/2*(3 * 4 * sin 30 độ)
Tính diện tích tam giác sử dụng công thức Heron
Trong đó:
- a, b, c: Lần lượt là độ dài các cạnh của tam giác.
- p: Nửa chu vi tam giác, bằng ½ tổng các cạnh của một tam giác.
Công thức tính diện tích tam giác khi biết bán kính đường tròn ngoại tiếp tam giác
Khi biết độ dài ba cạnh và bán kính đường tròn ngoại tiếp R của tam giác thì chúng ta áp dụng công thức sau:
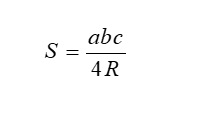
Trong đó:
- a, b, c: Lần lượt là độ dài các cạnh của tam giác.
- R: Bán kính đường tròn ngoại tiếp.
Công thức tính diện tích tam giác cân
Trước khi chúng ta đi vào công thức tính diện tích tam giác cân thì chúng ta cần phải hiểu rõ bản chất của tam giác cân là gì trước . Cụ thể như sau :
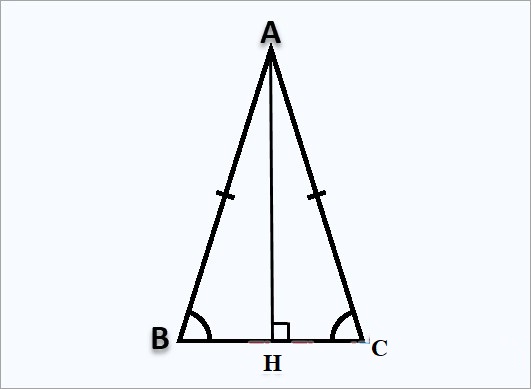
Định nghĩa
Tam giác cân là tam giác có hai cạnh bằng nhau và số đo hai góc ở đáy cũng bằng nhau.
Đặc điểm
Tam giác cân là tam giác bên trong đó có chứa các tính chất sau :
- Trong tam giác cân thì có 2 cạnh bằng nhau và 2 góc ở đáy bằng nhau.
- Tam giác vuông cân là tam giác vuông có 2 cạnh hay 2 góc ở đáy bằng nhau.
- Đường cao được hạ từ đỉnh xuống đáy trong tam giác cân cũng chính là đường trung tuyến và đường phân giác của tam giác đó.
Công thức tính chu vi tam giác cân
Hình tam giác cân có các tích chất của tam giác thường, do đó chu vi của nó cũng tính theo cách tương tự:
P = a + b + c
Trong đó:
- P: Chu vi tam giác.
- a, b, c: Lần lượt 3 cạnh của hình tam giác đó.
Công thức tính diện tích tam giác cân
Tính diện tích tam giác cân cũng dựa vào đường cao như công thức tính diện tích tam giác thường.
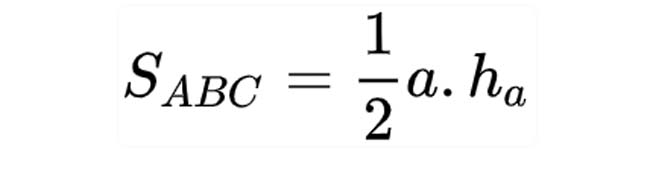
Trong đó :
- a : chiều dài cạnh bên của tam giác
- ha : là chiều cao từ đỉnh A nối vuông góc với cạnh đối diện
Ví dụ : Cho tam giác ACB cân tại C, gọi H là trung điểm của cạnh AB, cạnh AC = 8 cm, CH = 13 cm. Tính diện tích tam giác ACB.
Lời giải:
Bài toán cho biết chiều cao CH = 13 cm, cạnh đáy AC = 8 cm.
Áp dụng công thức tính diện tích ta có: S = 1⁄2 a.h = 1⁄2 x 13 x 8 = 52 cm2
=> Như thế thì diện tích của tam giá cân ACB sẽ là : 52cm2
Công thức tính diện tích tam giác đều
Theo cách nhận xét của cá nhân thì công thức tính diện tích tam giác đều thường sẽ đơn giản hơn và dễ dàng hơn so với cách tính diện tích của các hình tam giác khác.
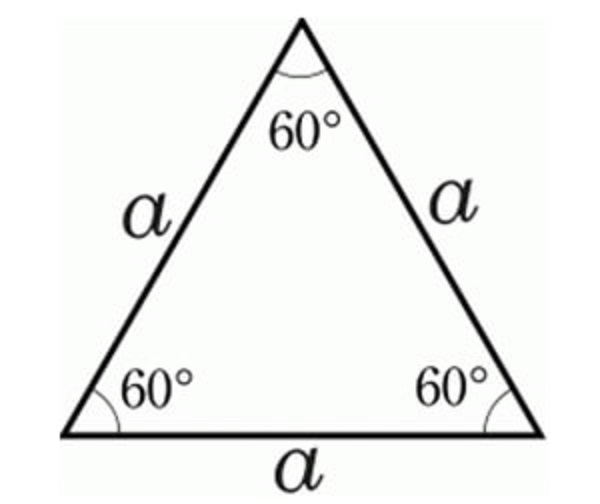
Định nghĩa
Hình tam giác đều là tam giác có 3 cạnh bằng nhau, 3 đường cao bằng nhau, 3 đường trung tuyến bằng nhau và 3 đường phân giác bằng nhau hoặc tương đương ba góc bằng nhau và bằng 60°
Đặc điểm
- Trong ta giác đều mỗi góc bằng 60 độ
- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
- Nếu một tam giác cân có một góc bằng 60 độ thì tam giác đó là tam giác đều
- Tam giác có ba cạnh bằng nhau là tam giác đều
- Tam giác có ba góc bằng nhau là tam giác đều
- Tam giác cân có một góc bằng 60 độ là tam giác đều
- Tam giác có hai góc bằng 60 độ là tam giác đều
Công thức tính chu vi
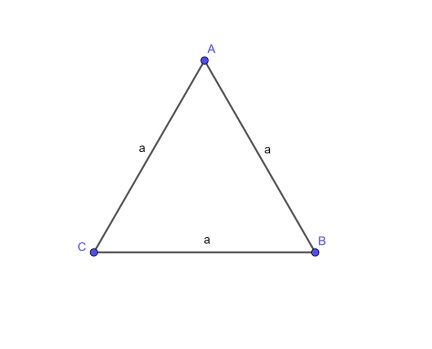
Do hình tam giác đều có 3 cạnh như nhau nên chu vi tam giác được tình bằng 3 lần cạnh bất kì trong tam giác đó
P = 3 * a
Trong đó:
- P: Chu vi tam giác đều.
- a: Chiều dài cạnh của tam giác.
Cách tính diện tích tam giác đều
Vì tam giác ABC đều nên đường cao kẻ từ đỉnh A trùng với đường trung tuyến kẻ đỉnh A của tam giác ABC
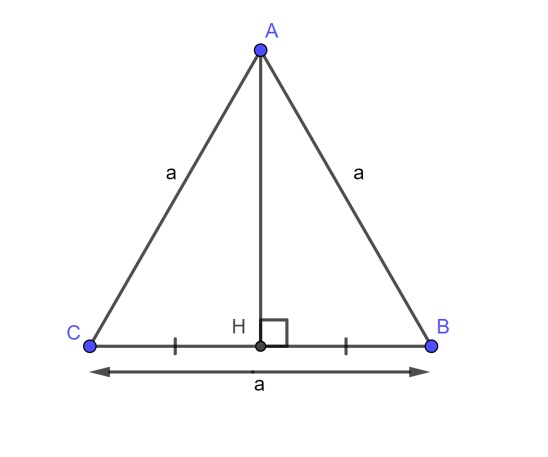
Công thức tính diện tích tam giác ABC là
Trong đó :
- AH : Chiều cao tam giác nối từ đỉnh A xuống BC
- BC : là chiều dài cạnh BC
Ngoài ra, các bạn áp dụng công thức Heron để tính:
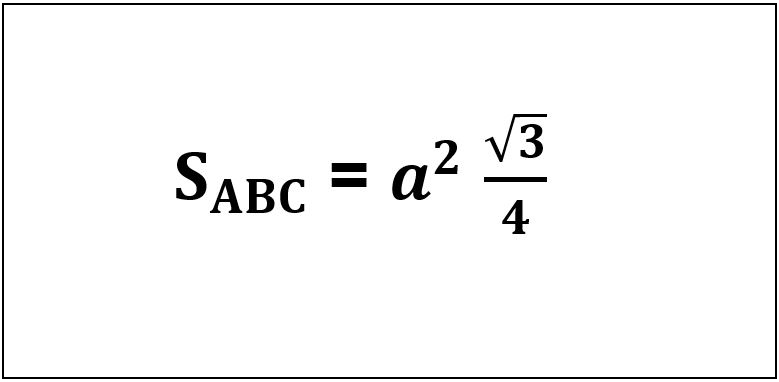
Trong đó:
- a: Độ dài các cạnh của tam giác đều.
Ví dụ : Có một tam giác đều ABC với chiều dài các cạnh bằng nhau là 8 cm, biết các góc của tam giác này đều bằng 60 độ. Hỏi diện tích tam giác đều ABC bằng bao nhiêu?
Trả lời : Do mỗi cạnh AB = AC = BC = 8cm nên ta có chiều dài cạnh a = 8cm.
Áp dụng công thức Heron thì chúng ta sẽ tính được diện tích tam giác đều ta có:
S = a2 x (√3)/4 = S = 64 x (√3)/4 = 64 x (√3)/4 = 64 x (1,732/4) = 27,712 cm2
Như vậy diện tích tam giác đều ABC = 27,712 cm2
Công thức tính diện tích tam giác vuông
Để mà tính được diện tích của tam giác vuông thì trước tiên chúng ta cần phải tìm hiểu thế nào là tam giác vuông và cách nhận biết về loại tam giác này trước nhé .
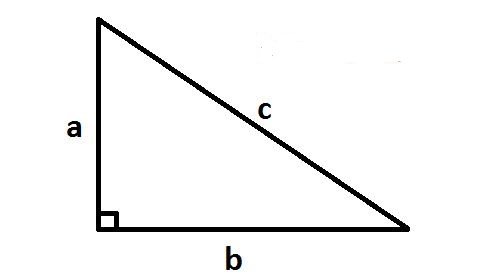
Định nghĩa
Hình tam giác vuông là tam giác có một góc vuông ( góc 900)
Cách nhận biết về tam giác vuông
- Tam giác có một góc vuông là tam giác vuông
- Tam giác có hai góc nhọn phụ nhau là tam giác vuông
- Tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia là tam giác vuông
- Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy là tam giác vuông
- Tam giác nội tiếp đường tròn có một cạnh là đường kính của đường tròn là tam giác vuông
Công thức tính chu vi
P = a + b + c
Trong đó:
- a, b, c là độ dài 3 cạnh tam giác
Công thức tính diện tích tam giác vuông
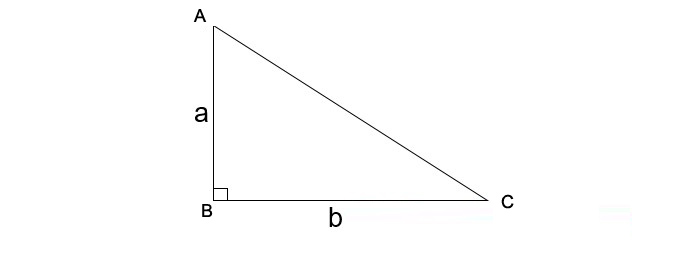
Để tính được điện tích tam giác vuông thì chúng ta có thể áp dụng công thức :
Trong đó :
- a , b : là chiều dài 2 cạnh góc vuông
Ví dụ: Cho tam giác vuông ABC , vuông tại góc B .Tính diện tích của tam giác vuông đó biết hai cạnh góc vuông lần lượt làAB = 4cm và BC = 7cm
Đáp án :
Áp dụng công thức trên về cách tính diện tích tam giác vuông thì chúng ta có thể tính như sau :
S = (4 x 7) : 2 = 14 (cm2)
=> Như vậy thì diện tích tam giác vuông ABC sẽ là : 14 cm2
Công thức tính diện tích tam giác vuông cân
Định nghĩa
Tam giác vuông cân là tam giác có 2 cạnh của góc vuông bằng nhau
Tính chất
Về tính chất của tam giác vuông cân thì chúng ta sẽ có 2 tính chất khác nhau :
Tính chất 1: Tam giác vuông cân có hai góc ở đáy bằng nhau và bằng 45 độ
Tính chất 2: Các đường cao, đường trung tuyến, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng 1 nửa cạnh huyền.
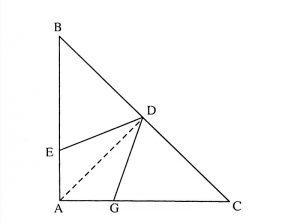
Ta có: Xét tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Ta có AD vừa là đường cao, vừa là đường phân giác, vừa là trung tuyến của BC. AD = BD = DC = 1/2BC
Công thức tính diện tích tam giác vuông cân
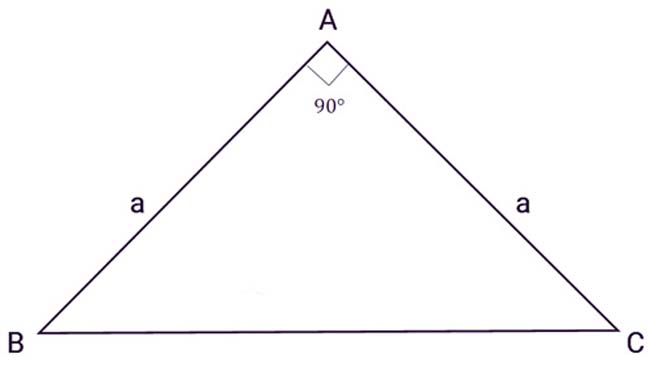
Công thức chuẩn để tính diện tích tam giác vuông cân như sau :
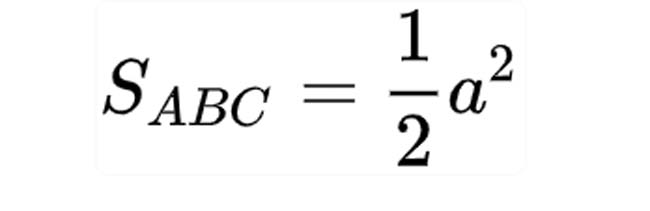
Ví dụ: Cho tam giác ABC vuông cân tại A, có AB = AC = 10cm. Tính diện tích tam giác ABC thông qua công thức tính diện tích tam giác ở trên.
Đáp án :
Do cạnh AB = AC = a = 10cm
Xét tam giác ABC vuông cân tại A, ta có:
S = (a2) : 2 = 100 : 2 = 50 cm2
Như thế ta có diện tích tam giác vuông cân ABC sẽ là : 50 cm2
Tổng kết :
Với tổng hợp các công thức tính diện tích tam giác vuông , tam giác thường , tam giác cân và tam giác vuông cân ở trên hi vọng mọi người có thể có thêm những kinh nghiệm và có thêm những kiến thức bổ tích mà Legoland đã tổng hợp và chắt lọc lên nhé .