Nhân ma trận (Matrix multiplication)
Thông thường, để đạt được độ phức tạp thuật toán như mong muốn, cách làm thường là tìm ra một thuật toán ban đầu làm cơ sở, rồi từ đó dùng các kỹ năng để giảm độ phức tạp của thuật toán. Trong bài viết này, tôi xin giới thiệu với bạn đọc một kỹ năng khá thông dụng: Nhân ma trận.
Định nghĩa
Ma trận là một mảng chữ nhật gồm các số, ký hiệu, hoặc biểu thức, sắp xếp theo hàng và cột mà mỗi ma trận tuân theo những quy tắc định trước. Các ô trong ma trận được gọi là các phần tử của ma trận. Các phần tử được xác định bằng 2 địa chỉ hàng i và cột j tương ứng (Kí hiệu là aij
).
Ma trận thường được viết trong dấu ngoặc vuông:

Độ lớn hay kích thước của ma trận được định nghĩa bằng số lượng hàng và cột. Một ma trận m hàng và n cột được gọi là ma trận (m×n), trong khi m và n
được gọi là chiều của nó.
- Ví dụ: Ma trận A
là ma trận (3×2)
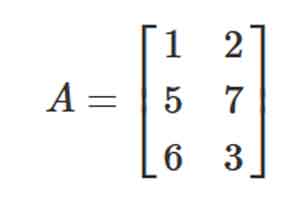
Ma trận vuông
Ma trận vuông là ma trận có số hàng và số cột bằng nhau. Ma trận (n×n) còn gọi là ma trận vuông cấp n. Các phần tử aii
tạo thành đường chéo chính của ma trận vuông.
- Ví dụ: Ma trận vuông cấp 3
(số hàng và số cột bằng 3)

Ma trận đơn vị (Identity Matrix)
Ma trận đơn vị In cấp n là một ma trận (n×n) trong đó mọi phần tử trên đường chéo chính bằng 1 và tất cả những phần tử khác đều bằng 0. Ma trận đơn vị cấp n cũng chính là ma trận vuông cấp n
.Ví dụ

Vector hàng và vector cột
Vector hàng hay ma trận hàng là một ma trận (1×n), tức là ma trận chỉ gồm một một hàng đơn gồm n
phần tử.
a=[a1 a2 … an]
Vector cột hay ma trận cột là một ma trận (m×1), tức là ma trận chỉ gồm một cột đơn gồm m phần tử.

Phép nhân ma trận
Phép nhân hai ma trận chỉ thực hiện được khi số lượng cột trong ma trận thứ nhất phải bằng số lượng hàng trong ma trận thứ hai. Ma trận kết quả, được gọi là tích ma trận, có số lượng hàng của ma trận đầu tiên và số cột của ma trận thứ hai.
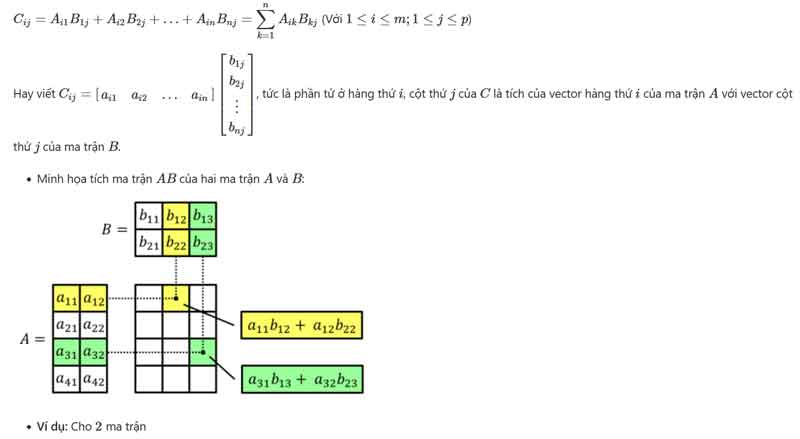
Nếu ma trận A có kích thước (m×n) và ma trận B có kích thước (n×p), thì ma trận tích C=A×B có kích thước (m×p), phần tử đứng ở hàng thứ i, cột thứ j xác định bởi công thức:

Tính chất của phép nhân ma trận
- Tính chất kết hợp: (AB)C=A(BC)
. Tính chất phân phối: (A+B)C=AC+BC, cũng như C(A+B)=CA+CB. Phép nhân ma trận không có tính chất giao hoán: Tích AB có thể xác định trong khi BA không nhất thiết phải xác định, tức là nếu A và B lần lượt có số chiều (m×n) và (n×p), và m≠p. Thậm chí khi cả hai tích này đều tồn tại thì chúng không nhất thiết phải bằng nhau, tức là AB≠BA.
- Ví dụ:

Khi thực hiện nhân một ma trận bất kì với ma trận đơn vị thì vẫn thu được kết quả của chính ma trận đó, tức là: AIn=ImA=A (với ma trận A kích thước (m×n) bất kỳ). Cũng chính vì tính chất này mà I có tên gọi là ma trận đơn vị.
Lũy thừa ma trận
Cho ma trận vuông A cấp n. Khi đó ta có phép tính ma trận A lũy thừa k (kí hiệu: Ak), với k là một số nguyên không âm.

Nhờ tính chất kết hợp của phép nhân ma trận nên ta có thể tính nhanh lũy thừa của ma trận tương tự như cách tính hàm mũ thông thường bằng phương pháp chia để trị (tính ak với a là số nguyên).
Cài đặt
Lưu ý: Khác với định nghĩa bên trên, trong cách cài đặt sau, các hàng và cột của ma trận được đánh số bắt đầu từ 0 để thuận tiện cho việc xử lí.
#include <bits/stdc++.h> using namespace std; using type = int; // Kiểu dữ liệu các phần tử của ma trận struct Matrix { vector <vector <type> > data; // Số lượng hàng của ma trận int row() const { return data.size(); } // Số lượng hàng của ma trận int col() const { return data[0].size(); } auto & operator [] (int i) { return data[i]; } const auto & operator[] (int i) const { return data[i]; } Matrix() = default; Matrix(int r, int c): data(r, vector <type> (c)) { } Matrix(const vector <vector <type> > &d): data(d) { // Kiểm tra các hàng có cùng size không và size có lớn hơn 0 hay không // Tuy nhiên không thực sự cần thiết, ta có thể bỏ các dòng /**/ đi /**/ assert(d.size()); /**/ int size = d[0].size(); /**/ assert(size); /**/ for (auto x : d) assert(x.size() == size); } // In ra ma trận. friend ostream & operator << (ostream &out, const Matrix &d) { for (auto x : d.data) { for (auto y : x) out << y << ‘ ‘; out << ‘n’; } return out; } // Ma trận đơn vị static Matrix identity(long long n) { Matrix a = Matrix(n, n); while (n-) a[n][n] = 1; return a; } // Nhân ma trận Matrix operator * (const Matrix &b) { Matrix a = *this; // Kiểm tra điều kiện nhân ma trận assert(a.col() == b.row()); Matrix c(a.row(), b.col()); for (int i = 0; i < a.row(); ++i) for (int j = 0; j < b.col(); ++j) for (int k = 0; k < a.col(); ++k) c[i][j] += a[i][k] * b[k][j]; return c; } // Lũy thừa ma trận Matrix pow(long long exp) { // Kiểm tra điều kiện lũy thừa ma trận (là ma trận vuông) assert(row() == col()); Matrix base = *this, ans = identity(row()); for (; exp > 0; exp >>= 1, base = base * base) if (exp & 1) ans = ans * base; return ans; } }; int main(){ Matrix a({ {1, 2}, {3, 4} }); Matrix b({ {0, 10, 100}, {1, 1, 10} }); cout << a * b << ‘n’; // 2 12 120 // 4 34 340 cout << a.pow(3) << ‘n’; // 37 54 // 81 118 b = a; cout << b << ‘n’; // 1 2 // 3 4 b = Matrix::identity(3); cout << b << ‘n’; // 1 0 0 // 0 1 0 // 0 0 1 b = Matrix(2, 3); cout << b << ‘n’; // 0 0 0 // 0 0 0 Matrix c(3, 2); cout << c << ‘n’; // 0 0 // 0 0 // 0 0 }
Đánh giá
Ngoài cách cài đặt tính lũy thừa ma trên như trên thì ta còn có thể cài đặt theo một cách khác bằng đệ quy như sau:
Matrix pow(long long exp) { Matrix base = *this; if (exp == 0) return identity(base.row()); if (exp == 1) return base; Matrix p = pow(exp >> 1); p = p * p; if (exp & 1) return p * base; return p; }
Độ phức tạp

Ví dụ 1
Chúng ta hãy cùng xem xét một ví dụ kinh điển nhất trong ứng dụng của phép nhân ma trận.
Bài toán
Cho một hình chữ nhật kích thước 2×N (1≤N≤109). Hãy đếm số cách lát các viên gạch nhỏ kích thước 1×2 và 2×1 vào hình trên sao cho không có phần nào của các viên gạch nhỏ thừa ra ngoài, cũng không có vùng diện tích nào của hình chữ nhật không được lát.
Phân tích
Gọi Fi là số cách lát các viên gạch nhỏ vào hình chữ nhật kích thước 2×i
. Ta có:
- Nếu sử dụng viên gạch kích thước 1×2
thì Fi=Fi−2. Nếu sử dụng viên gạch kích thước 2×1 thì Fi=Fi−1
- .
⇒Fi=Fi−1+Fi−2.
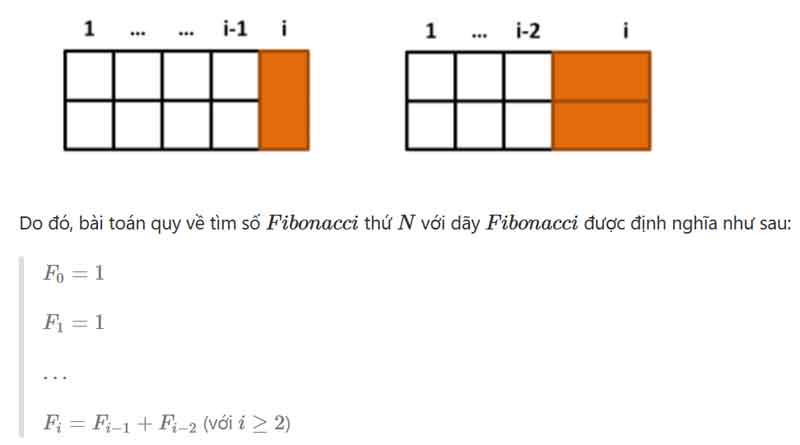
Hiển nhiên cách làm thông thường là tính lần lượt các Fi. Tuy nhiên, cách làm này hoàn toàn không hiệu quả với N lên đến 109
, và ta cần một cách tiếp cận khác.
Ta xét các lớp số:

Ta hình dung mỗi lớp là một ma trận (2×1). Tiếp đó, ta sẽ biến đổi từ lớp i−1 đến lớp i. Sau mỗi lần biến đổi như vậy, ta tính thêm được một giá trị Fi. Để thực hiện phép biến đổi này, chú ý là các số ở lớp sau chỉ phụ thuộc vào lớp ngay trước nó theo các phép cộng, ta tìm được cách biến đổi bằng nhân ma trận:

Vậy bài toán trên được đưa về dạng nhân ma trận. FN được tính dựa vào phép lũy thừa của ma trận A
.Cài đặt
Lưu ý: Khác với định nghĩa bên trên. Trong cách cài đặt sau, các hàng và cột của ma trận được đánh số bắt đầu từ 0
để thuận tiện cho việc xử lí.
#include <bits/stdc++.h> using namespace std; const int mod = 111539786; using type = int; struct Matrix { vector <vector <type> > data; int row() const { return data.size(); } int col() const { return data[0].size(); } auto & operator [] (int i) { return data[i]; } const auto & operator[] (int i) const { return data[i]; } Matrix() = default; Matrix(int r, int c): data(r, vector <type> (c)) { } Matrix(const vector <vector <type> > &d): data(d) { } friend ostream & operator << (ostream &out, const Matrix &d) { for (auto x : d.data) { for (auto y : x) out << y << ‘ ‘; out << ‘n’; } return out; } static Matrix identity(long long n) { Matrix a = Matrix(n, n); while (n-) a[n][n] = 1; return a; } Matrix operator * (const Matrix &b) { Matrix a = *this; assert(a.col() == b.row()); Matrix c(a.row(), b.col()); for (int i = 0; i < a.row(); ++i) for (int j = 0; j < b.col(); ++j) for (int k = 0; k < a.col(); ++k){ c[i][j] += 1ll * a[i][k] % mod * (b[k][j] % mod) % mod; c[i][j] %= mod; } return c; } Matrix pow(long long exp) { assert(row() == col()); Matrix base = *this, ans = identity(row()); for (; exp > 0; exp >>= 1, base = base * base) if (exp & 1) ans = ans * base; return ans; } }; int main(){ Matrix a({ {1, 1}, {1, 0} }); int t; cin >> t; while (t-) { int n; cin >> n; Matrix tmp = a.pow(n – 1); cout << (tmp[0][0] + tmp[0][1]) % mod << ‘n’; } }
Đánh giá
Độ phức tạp
Độ phức tạp của thuật toán là O(T×23×logN). Với T là số lượng bộ test.
Ví dụ 2
Bây giờ chúng ta sẽ cùng xem xét một ví dụ tổng quát hơn của ví dụ 1.
Bài toán



Cài đặt
Lưu ý: Khác với định nghĩa bên trên. Trong cách cài đặt sau, các hàng và cột của ma trận được đánh số bắt đầu từ 0 để thuận tiện cho việc xử lí.
#include <bits/stdc++.h> using namespace std; const int mod = 1e9; using type = int; struct Matrix { vector <vector <type> > data; int row() const { return data.size(); } int col() const { return data[0].size(); } auto & operator [] (int i) { return data[i]; } const auto & operator[] (int i) const { return data[i]; } Matrix() = default; Matrix(int r, int c): data(r, vector <type> (c)) { } Matrix(const vector <vector <type> > &d): data(d) { } friend ostream & operator << (ostream &out, const Matrix &d) { for (auto x : d.data) { for (auto y : x) out << y << ‘ ‘; out << ‘n’; } return out; } static Matrix identity(long long n) { Matrix a = Matrix(n, n); while (n-) a[n][n] = 1; return a; } Matrix operator * (const Matrix &b) { Matrix a = *this; assert(a.col() == b.row()); Matrix c(a.row(), b.col()); for (int i = 0; i < a.row(); ++i) for (int j = 0; j < b.col(); ++j) for (int k = 0; k < a.col(); ++k){ c[i][j] += 1ll * a[i][k] % mod * (b[k][j] % mod) % mod; c[i][j] %= mod; } return c; } Matrix pow(long long exp) { assert(row() == col()); Matrix base = *this, ans = identity(row()); for (; exp > 0; exp >>= 1, base = base * base) if (exp & 1) ans = ans * base; return ans; } }; int b[15], c[15]; int main(){ int t; cin >> t; while (t-) { int n, k; cin >> k; for (int i = 1; i <= k; ++i) cin >> b[i]; for (int i = 1; i <= k; ++i) cin >> c[i]; cin >> n; if (n <= k) { cout << b[n] << ‘n’; continue; } // Xây dựng ma trận cơ sở Matrix base(k, 1); for (int i = 1; i <= k; ++i) base[i – 1][0] = b[i]; // Xây dựng ma trận hệ số D Matrix d(k, k); for (int i = 0; i < k – 1; ++i) d[i][i + 1] = 1; for (int i = 0; i < k; ++i) d[k – 1][i] = c[k – i]; Matrix ans = d.pow(n – k) * base; cout << ans[k – 1][0] << ‘n’; } }
Đánh giá
Độ phức tạp
Độ phức tạp của thuật toán là O(t×k3×log(n−k)). Với t là số lượng bộ test.
Ví dụ 3
Bài toán
Người ta mới tìm ra một loại vi khuẩn mới. Chúng sống thành N bầy (N≤100), đánh số từ 0 đến N−1. Ban đầu, mỗi bầy này chỉ có một con vi khuẩn. Tuy nhiên, mỗi giây, số lượng vi khuẩn trong các bầy lại có sự thay đổi: Một số vi khuẩn có thể chết đi, sinh sản thêm, hoặc di chuyển sang bầy khác. Những thay đổi này luôn tuân theo một quy luật có sẵn. Tại mỗi giây chỉ xảy ra đúng một quy luật. Các quy luật này được thực hiện nối tiếp nhau và theo chu kỳ. Có nghĩa là, nếu đánh số các quy luật từ 0 đến M−1, tại giây thứ S thì quy luật được áp dụng sẽ là (S−1)modM (M≤1000)
.Nhiệm vụ của bạn là tìm xem, với một bộ các quy luật cho trước, sau T đơn vị thời gian (T≤1018), mỗi bầy có bao nhiêu vi khuẩn.
Các loại quy luật có thể có:

Phân tích
Cách làm đơn giản nhất là chúng ta mô phỏng lại số lượng vi khuẩn trong mỗi bầy qua từng đơn vị thời gian. Cách làm này có độ phức tạp O(T×N×k) với O(k) là độ phức tạp cho xử lý số lớn. Cách này không thể chạy được với T
lớn.
Ta hình dung số lượng vi khuẩn trong mỗi bầy trong một đơn vị thời gian là một dãy số. Như vậy, mỗi quy luật cho trước thực chất là một phép biến đổi từ một dãy số thành một dãy số mới, và ta hoàn toàn có thể thực hiện biến đổi này bằng một phép nhân ma trận.
Cụ thể hơn, ta coi số lượng vi khuẩn trong N bầy tại một thời điểm xác định là một ma trận 1×N, và mỗi phép biến đổi là một ma trận N×N
. Khi áp dụng mỗi phép biến đổi, ta nhân hai ma trận nói trên với nhau.
Bây giờ, xét trường hợp N=4, các ma trận tương ứng với các phép biến đổi lần lượt được mô tả như sau:
-
Biến đổi: A 2 0
1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1
-
Biến đổi: B 2 6
1 0 0 0 0 1 0 0 0 0 6 0 0 0 0 1
-
Biến đổi: C 1 3
1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1
-
Biến đổi: D 1 3
1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0
-
Biến đổi: E 1 3
1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0
-
Biến đổi: F 0 0
0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0
Cũng như các bài toán trước, ta sẽ cố gắng áp dụng việc tính toán lũy thừa, kết hợp với phép nhân ma trận để giảm độ phức tạp từ T xuống logT
. Tuy nhiên, có thể thấy việc sử dụng phép lũy thừa trong bài toán này phần nào phức tạp hơn bởi các ma trận được cho không giống nhau. Để giải quyết vấn đề này, ta làm như sau:
Gọi X1,X2,…,Xm
là các ma trận tương ứng với các phép biến đổi được cho.
Đặt X=X1×X2×…×Xm
.
Đặt S=[1,1,…,1]
(dãy số lượng vi khuẩn tại thời điểm đầu tiên).
Như vậy, Y=S×Xt×X1×X2×…×Xr là ma trận thể hiện số lượng vi khuẩn tại thời điểm M×t+r
.
Như vậy, thuật toán đến đây đã rõ. Ta phân tích T=M×t+r, nhờ đó, ta có thể giải quyết bài toán trong O(N3×M) cho bước tính ma trận X và O(N3×(logT/M+M)) cho bước tính Y. Bài toán được giải quyết.
Ví dụ 4
Bài toán
Số đẹp là một số nguyên dương với bất kỳ chữ số lẻ nào (1,3,5,7,9) đều xuất hiện lẻ lần nếu nó xuất hiện và bất kỳ chữ số chẵn nào (0,2,4,6,8) cũng xuấn hiện chẵn lần nếu nó xuất hiện. Ví dụ số 141222124 là một số đẹp. Gọi fn là số lượng số đẹp có không quá n chữ số. Yêu cầu với một số n (1≤n≤1018) tính fnmod1000000123.
Phân tích
Cách làm đơn giản nhất là ta sử dụng quy hoạch động với 4 trạng thái:

Ta không phải lưu số chữ số chẵn đã xuất hiện vì nếu chữ số chẵn đó không xuất hiện thì cũng đã được tính vào trường hợp nó đã xuất hiện chẵn lần rồi.
Do đó, ta có công thức quy hoạch động theo như code sau:
#include <bits/stdc++.h> using namespace std; const int mod = 1e9 + 123; int n; int dp[10005][6][6][6]; long long digit_dp(int added, int ewoc, int owoc, int added_odd) { // Khi đã chọn đủ n chữ số if (added == n) return (!ewoc && owoc == added_odd); if (dp[added][ewoc][owoc][added_odd] != -1) return dp[added][ewoc][owoc][added_odd]; long long cur = 0; // Thêm vào 1 số chẵn đã xuất hiện lẻ lần if (ewoc) cur += digit_dp(added + 1, ewoc – 1, owoc, added_odd) * ewoc; // Thêm vào 1 số chẵn đã xuất hiện chẵn lần if (ewoc < 5) cur += digit_dp(added + 1, ewoc + 1, owoc, added_odd) * (5 – ewoc); // Thêm vào 1 số lẻ chưa xuất hiện if (added_odd < 5) cur += digit_dp(added + 1, ewoc, owoc + 1, added_odd + 1) * (5 – added_odd); // Thêm vào 1 số lẻ đã xuất hiện lẻ lần if (owoc) cur += digit_dp(added + 1, ewoc, owoc – 1, added_odd) * owoc; // Thêm vào 1 số lẻ đã xuất hiện chẵn lần if (owoc < added_odd) cur += digit_dp(added + 1, ewoc, owoc + 1, added_odd) * (added_odd – owoc); // Không nhất thiết phải chọn đủ n chữ số if (!ewoc && owoc == added_odd) ++cur; return dp[added][ewoc][owoc][added_odd] = cur % mod; } int solve(int n1) { n = n1; for (int i = 0; i < n; ++i) for (int j = 0; j < 6; ++j) for (int k = 0; k < 6; ++k) for (int l = 0; l < 6; ++l) dp[i][j][k][l] = -1; // Loại trường hợp chọn phải số 0 vô nghĩa bằng cách đặt trước chữ số đầu tiên long long tmp1 = digit_dp(1, 1, 0, 0) * 4; long long tmp2 = digit_dp(1, 0, 1, 1) * 5; return (tmp1 + tmp2) % mod; } int main(){ int n1; while (cin >> n1) cout << solve(n1) << ‘n’; }
Bạn có thể tìm hiểu thêm về kĩ thuật quy hoạch động sử dụng đệ quy có nhớ (Top-Down) tại đây.
Vì số chữ số lẻ đã xuất hiện lẻ lần không được vượt quá số chữ số lẻ đã xuất hiện, nên ta tối ưu được số trạng thái xuống còn khoảng 6×6×6 / 2. Khi đó, độ phức tạp của thuật toán trên sẽ là O(n×(6×6×6 / 2))
.Tuy nhiên, với n≤1018
thì hiển nhiên thuật toán trên sẽ bị quá cả thời gian lẫn bộ nhớ.
Do đó, ta cần phải cải tiến thuật toán bằng lũy thừa ma trận với số trạng thái cho 1 lớp dp là 6×6×6 / 2=108
.Tối ưu hóa thuật toán bằng cách tách n thành các lũy thừa của 2 sau đó sử dụng các ma trận hệ số tương ứng đã tính toán trước để tính nhanh kết quả.
Cài đặt
Lưu ý: Trong cách cài đặt sau, các hàng và cột của ma trận được đánh số bắt đầu từ 0 để thuận tiện cho việc xử lí.
#include <bits/stdc++.h> using namespace std; const int mod = 1e9 + 123; using type = int; struct Matrix { vector <vector <type> > data; int row() const { return data.size(); } int col() const { return data[0].size(); } auto & operator [] (int i) { return data[i]; } const auto & operator[] (int i) const { return data[i]; } Matrix() = default; Matrix(int r, int c): data(r, vector <type> (c)) { } Matrix(const vector <vector <type> > &d): data(d) { } friend ostream & operator << (ostream &out, const Matrix &d) { for (auto x : d.data) { for (auto y : x) out << y << ‘ ‘; out << ‘n’; } return out; } Matrix operator * (const Matrix &b) { Matrix a = *this; assert(a.col() == b.row()); Matrix c(a.row(), b.col()); for (int i = 0; i < a.row(); ++i) for (int j = 0; j < b.col(); ++j) for (int k = 0; k < a.col(); ++k){ c[i][j] += 1ll * a[i][k] % mod * (b[k][j] % mod) % mod; c[i][j] %= mod; } return c; } }; int last; int odd_id[6][6]; Matrix coef, base; vector <Matrix> coef_pow; int id(int ewoc, int owoc, int added_odd) { assert(owoc <= added_odd); return ewoc * last + odd_id[added_odd][owoc]; }; // Xây dựng ma trận hệ số void build_coef() { int ans_id = id(5, 5, 5) + 1; coef = Matrix(ans_id + 1, ans_id + 1); for (int added_odd = 0; added_odd <= 5; ++added_odd) for (int ewoc = 0; ewoc <= 5; ++ewoc) for (int owoc = 0; owoc <= added_odd; ++owoc) { int cur_id = id(ewoc, owoc, added_odd); if (ewoc) coef[id(ewoc – 1, owoc, added_odd)][cur_id] += ewoc; if (ewoc < 5) coef[id(ewoc + 1, owoc, added_odd)][cur_id] += 5 – ewoc; if (added_odd < 5) coef[id(ewoc, owoc + 1, added_odd + 1)][cur_id] += 5 – added_odd; if (owoc) coef[id(ewoc, owoc – 1, added_odd)][cur_id] += owoc; if (owoc < added_odd) coef[id(ewoc, owoc + 1, added_odd)][cur_id] += added_odd – owoc; if (!ewoc && owoc == added_odd) ++coef[ans_id][cur_id]; } coef[ans_id][ans_id] = 1; } // Xây dựng ma trận cơ sở void build_base() { int ans_id = id(5, 5, 5) + 1; base = Matrix(ans_id + 1, 1); base[id(1, 0, 0)][0] = 4; base[id(0, 1, 1)][0] = 5; } int main() { last = 0; for (int added_odd = 0; added_odd <= 5; ++added_odd) for (int owoc = 0; owoc <= added_odd; ++owoc) odd_id[added_odd][owoc] = ++last; build_base(); build_coef(); // Tính lũy thừa ma trận hệ số tương ứng với lũy thừa của 2 coef_pow.push_back(coef); for (int i = 1; i <= 60; ++i) coef_pow.push_back(coef_pow[i – 1] * coef_pow[i – 1]); long long n; while (cin >> n) { Matrix ans = base; for (int i = 0; n > 0; n >>= 1, ++i) if (n & 1) ans = coef_pow[i] * ans; cout << ans[ans.row() – 1][0] << ‘n’; } }
Đánh giá
Độ phức tạp
Ta mất độ phức tạp O(6×6×6 / 2)
cho việc xây dựng ma trận hệ số.
Vì ma trận kết quả có kích thước là ((số trạng thái) × 1) chứ không phải là ((số trạng thái) × (số trạng thái)), nên độ phức tạp nhân ma trận trong lúc tính kết quả là (số trạng thái)2 chứ không phải (số trạng thái)3. Nên độ phức tạp của thuật toán là O(log1018×1082)
.
Ngoài ra, kể cả khi ta không giảm số trạng thái xuống còn khoảng 6×6×6 / 2
thì thuật toán này vẫn đủ tốt.
Ví dụ 5
Bài toán

Phân tích
Bằng phương pháp quy nạp, ta có thể dễ dàng chứng minh 2
định lý sau:
- Định lí 1: Cho dãy f1=a,f2=b,…,fn=fn−1+fn−2 (n>2)
thì fn=b×Fn−1+a×Fn−2 (n>2), trong đó Fi là số hạng thứ i của dãy Fibonacci
- Định lí 2: Cho dãy f1=a,f2=b,…,fn=fn−1+fn−2 (n>2)
thì f1+f2+…+fn=fn+2−b .
a còn có tính chất của dãy Fibonacci
như sau:
- Ta có thể chuyển đổi hai số hạng đầu tiên của dãy Fibonacci
- để nhận được một dãy mới.
- Gọi f1
, f2 là hai dãy mới được tạo thành từ việc chuyển đổi hai số hạng đầu tiên của dãy Fibonacci, và dãy f3 được xác định như sau f3 i=f1 i+f2 i (i≥1) thì dãy f3 vẫn tuân theo công thức truy hồi fn=fn−1+fn−2.
Sau khi sử dụng các tính chất trên, bài toán trở thành một hoạt động rất cơ bản của cây phân đoạn (Cây IT – Interval Tree / Segment Tree). Với mỗi nút của cây phân đoạn lưu lại hai giá trị đầu tiên của dãy.
Ở bài viết này, tôi sẽ sử dụng phương pháp nhân ma trận kết hợp với cây phân đoạn để giải quyết bài toán. Với mỗi nút của cây sẽ lưu lại ma trận hệ số của dãy Fibonacci
.Cài đặt
Lưu ý: Trong cách cài đặt sau, các hàng và cột của ma trận được đánh số bắt đầu từ 0
để thuận tiện cho việc xử lí.
#include <bits/stdc++.h> using namespace std; const int mod = 1e9 + 9; struct Matrix { static const int size = 2; int row, col; int data[size][size]; Matrix(){ row = col = size; for (int i = 0; i < row; ++i) fill_n(data[i], col, 0); }; auto & operator [] (int i) { return data[i]; } const auto & operator[] (int i) const { return data[i]; } // Phép cộng ma trận Matrix operator + (const Matrix &b) { Matrix a = *this; for (int i = 0; i < a.row; ++i) for (int j = 0; j < a.col; ++j) a[i][j] = (a[i][j] + b[i][j]) % mod; return a; } Matrix operator * (const Matrix &b) { Matrix a = *this, c; for (int i = 0; i < a.row; ++i) for (int j = 0; j < b.col; ++j) for (int k = 0; k < a.col; ++k) { c[i][j] += 1ll * a[i][k] * (b[k][j] % mod) % mod; c[i][j] %= mod; } return c; } // Kiểm tra xem tất cả phần tử của ma trận có bằng 0 hay không bool iszero() { for (int i = 0; i < size; ++i) for (int j = 0; j < size; ++j) if (data[i][j]) return false; return true; } }; const int maxN = 3e5 + 10; int n, m; int a[maxN]; int st[4 * maxN]; Matrix lazy[4 * maxN], base_pow[4 * maxN]; void build(int id, int l, int r) { if (l == r) { st[id] = a[l]; return; } int mid = (l + r) >> 1; build(id << 1, l, mid); build(id << 1 | 1, mid + 1, r); st[id] = (st[id << 1] + st[id << 1 | 1]) % mod; } void fix(int id, int l, int r) { if (lazy[id].iszero()) return; long long a = lazy[id][0][1]; long long b = lazy[id][0][0]; int tmp = (r – l + 1) + 2; st[id] += (b * base_pow[tmp – 1][0][1] + a * base_pow[tmp – 2][0][1] – b) % mod; st[id] %= mod; if (l != r) { int mid = (r – l) >> 1; lazy[id << 1] = lazy[id << 1] + lazy[id]; lazy[id << 1 | 1] = lazy[id << 1 | 1] + lazy[id] * base_pow[mid + 1]; } lazy[id] = Matrix(); } void update(int id, int l, int r, int u, int v) { fix(id, l, r); if (l > v || r < u) return; if (l >= u && r <= v) { lazy[id] = lazy[id] + base_pow[l – u + 1]; fix(id, l, r); return; } int mid = (l + r) >> 1; update(id << 1, l, mid, u, v); update(id << 1 | 1, mid + 1, r, u, v); st[id] = (st[id << 1] + st[id << 1 | 1]) % mod; } int get(int id, int l, int r, int u, int v) { fix(id, l, r); if (l > v || r < u) return 0; if (l >= u && r <= v) return st[id]; int mid = (l + r) >> 1; int g1 = get(id << 1, l, mid, u, v); int g2 = get(id << 1 | 1, mid + 1, r, u, v); return (g1 + g2) % mod; } main() { cin >> n >> m; for (int i = 1; i <= n; ++i) cin >> a[i]; build(1, 1, n); // Xây dựng lũy thừa ma trận hệ số của dãy Fibonacci base_pow[1][0][0] = base_pow[1][0][1] = base_pow[1][1][0] = 1; for (int i = 2; i <= n + 2; ++i) base_pow[i] = base_pow[i – 1] * base_pow[1]; while (m-) { int t, l, r; cin >> t >> l >> r; if (t == 1) update(1, 1, n, l, r); else cout << get(1, 1, n, l, r) << ‘n’; } }
Đánh giá
Ở thuật toán này, ta sử dụng mảng tĩnh để lưu ma trận thay vì sử dụng mảng động (Vector) như những bài toán trước. Vì số lượng ma trận phải lưu lên đến 4×n
nên việc khai báo mảng động sẽ khiến thuật toán bị quá thời gian.
Độ phức tạp
Với mỗi truy vấn, ta sẽ mất độ phức tạp O(logN)
cho các thao tác trên cây phân đoạn. Và ta cũng mất thêm O(22) và O(23) cho các phép cộng và phép nhân ma trận. Nhìn chung, độ phức tạp của thuật toán là O(m×logN×23).
Ví dụ 6
Phép nhân ma trận cộng tối thiểu (Min-plus matrix multiplication)
Nhận thấy rằng, ta hoàn toàn có thể thay thế phép nhân và phép cộng trong định nghĩa phép nhân ma trận, chỉ cần đảm bảo giữ nguyên tính chất kết hợp. Cụ thể hơn, với A và B là hai ma trận vuông cấp n, thay vì
ta có thể định nghĩa phép “nhân ma trận” mới như sau:
Nó còn được gọi là phép nhân ma trận cộng tối thiểu hay tích ma trận khoảng cách.
Từ đó, ta có thể thu được một lớp các bài toán khác. Sau đây là một ví dụ minh hoạ cho nhóm các bài toán này.
Bài toán
Cho đồ thị có hướng có trọng số gồm N đỉnh và M cạnh. Hãy tìm đường đi ngắn nhất xuất phát từ đỉnh 1 và kết thúc tại đỉnh N đi qua chính xác k
cạnh.
- N≤100
- 1≤M≤N(N−1)
- 1≤k≤109
Phân tích
Gọi ma trận C(k) kích thước N×N, với C(k)[i,j] là độ dài đường đi ngắn nhất từ i đến j đi qua đúng k cạnh.
Xét ma trận A là ma trận kề của đồ thị đã cho. Ta có:
C(1)=A
- C(2)[i,j]=min(A[i,u]+A[u,j])
với 1≤u≤N
- C(k)[i,j]=min(C(k−1)[i,u]+A[u,j])
với 1≤u≤N
Như vậy, nếu ta thay phép nhân và phép cộng trong nhân ma trận thông thường lần lượt bởi phép cộng và phép lấy min, ta thu được một phép ”nhân ma trận” mới, ký hiệu là ⋆ , thì:
C(1)=A
C(2)=C(1)⋆C(1)=A⋆C(1)
C(3)=C(1)⋆C(2)=A⋆C(2)
C(4)=C(1)⋆C(3)=A⋆C(3)
…
C(k)=C(1)⋆C(k−1)=A⋆C(k−1)
Do đó, C(k)=Ak
Như vậy, bài toán được đưa về bài toán tính lũy thừa của một ma trận, ta hoàn toàn có thể giải tương tự các ví dụ trước. Cài đặt phép nhân ma trận mới này hoàn toàn không phức tạp hơn cài đặt phép nhân ma trận thông thường. Việc cài đặt xin nhường lại cho bạn đọc.
Phép toán kết hợp và độ phức tạp tính toán
Nhân tổ hợp dãy ma trận
Trong phần Cài đặt, ta đã có thuật toán nhân hai ma trận A
kích cỡ (m×n) và B kích cỡ (n×p) cần độ phức tạp O(m×n×p). Giả sử ta có thêm ma trận C có kích cỡ (p×q) và ta cần tính tích A×B×C. Xét hai cách thực hiện phép nhân này:
Cách 1: (A×B)×C thực hiện nhân A và B rồi nhân với C cần độ phức tạp O(m×n×p)+O(m×p×q)=O(m×p×(n+q))
Cách 2: A×(B×C) thực hiện nhân B và C rồi nhân với A cần độ phức tạp O(n×p×q)+O(m×n×q)=O(n×q×(m+p)).
Như vậy là hai cách thực hiện khác nhau cần hai độ phức tạp khác nhau. Ví dụ:
- Cho m=n=500,p=1000,q=2
. Cách 1 sẽ cần tới 500×1000×(500+2)=251×106 phép tính, trong khi cách 2 chỉ cần 500×2×(500+1000)=1.5×106 phép tính, nghĩa là cách 1 chậm hơn cách 2 tới gần 200 lần.
Khi độ dài của dãy ma trận tăng lên, sự khác biệt có thể còn lớn hơn nữa. Ví dụ trên đã cho thấy rằng trong một số trường hợp thứ tự thực hiện phép nhân ma trận có ý nghĩa rất lớn đối với việc tìm lời giải của các bài toán.
Giải thuật Freivalds kiểm tra tích hai ma trận
Giải thuật Freivalds là một ví dụ điển hình về việc áp dụng thứ tự thực hiện phép nhân ma trận để giảm độ phức tạp tính toán của phép nhân một dãy ma trận. Bài toán đặt ra là cho ba ma trận vuông A,B,C có kích cỡ N×N với N≤1000. Ta cần kiểm tra xem C có phải là tích của A và B, nói cách khác ta cần kiểm tra A×B=C có phải là mệnh đề đúng hay không (đây chính là bài VMATRIX – VNOI Marathon 2014).
Phân tích
Cách làm thông thường là nhân trực tiếp hai ma trận A,B
rồi so sánh kết quả với C. Như đánh giá trong phần Cài đặt, độ phức tạp của cách làm này là O(N3), với N=1000 thì cách làm này không đủ nhanh. Giải thuật Freivalds thực hiện việc kiểm tra thông qua thuật toán xác suất kiểu Monte Carlo với k lần thử cho xác suất kết luận sai là xấp xỉ 2−k, mỗi lần thử có độ phức tạp O(N2). Các bước cơ bản của một phép thử Freivalds như sau:
Sinh ngẫu nhiên một ma trận v kích cỡ (N×1) với các phần tử chỉ nhận giá trị 0 hoặc 1
- Tính hiệu P=A×B×v−C×v
. Dễ thấy rằng P là ma trận kích cỡ N×1
- Trả về True nếu P chỉ gồm phần tử 0 (bằng với vector 0) và False nếu ngược lại.
Ta thực hiện k lần thử, nếu gặp phép thử trả về False thì ta kết luận là A×B≠C. Ngược lại nếu sau k phép thử mà luôn thấy True thì ta kết luận A×B=C. Vì xác suất lỗi giảm theo hàm mũ của k nên thông thường chỉ cần chọn k vừa đủ là sẽ thu được xác suất đúng rất cao (k=5 với bài VMATRIX ở trên). Một nhận xét quan trọng khác là cận trên của đánh giá xác suất kiểm tra lỗi không phụ thuộc vào kích cỡ N của ma trận được cho mà chỉ phụ thuộc vào số lần thực hiện phép thử.
Xét bước thứ 2, ta thấy rằng phép thử Freivalds chỉ có ý nghĩa nếu như ta có thể thực hiện phép nhân A×B×v trong thời gian O(N2) (vì phép nhân C×v đã đạt sẵn O(N2) rồi). Thay vì thực hiện tuần tự từ trái qua phải sẽ cần O(N3), ta thực hiện theo thứ tự A×(B×v). Vì kết quả của phép nhân B và v là một ma trận (N×1) nên độ phức tạp tổng cộng sẽ là O(N2). Trên tất cả các phép thử, độ phức tạp là O(k×N2).
Phép nhân ma trận
Trong đại số tuyến tính, ma trận đóng một vai trò quan trọng trong việc xử lý các khái niệm khác nhau. Một ma trận là một hình chữ nhật mảng hoặc bảng số, biểu tượng, hoặc biểu thức, sắp xếp theo hàng và cột trong toán học. Chúng ta có thể thực hiện các phép toán khác nhau trên ma trận như cộng, trừ, nhân, v.v. Trong bài này, bạn sẽ học cách nhân một ma trận với một ma trận khác, thuật toán, công thức, phép nhân ma trận 2 × 2 và 3 × 3 với các ví dụ chi tiết.
Định nghĩa phép nhân ma trận
Phép nhân ma trận, còn được gọi là tích ma trận và phép nhân hai ma trận, tạo ra một ma trận duy nhất. Nó là một loại hoạt động nhị phân .
Nếu A và B là hai ma trận thì tích của hai ma trận A và B được ký hiệu là:
X = AB
Do đó, tích của hai ma trận là tích chấm của hai ma trận.
Phép nhân ma trận bằng Vô hướng
Phép nhân một số nguyên với một ma trận chỉ đơn giản là một phép nhân vô hướng .
Chúng ta biết rằng ma trận là một mảng số. Nó bao gồm các hàng và cột. Nếu bạn nhân một ma trận với một giá trị vô hướng, thì nó được gọi là phép nhân vô hướng. Một trường hợp khác là có thể nhân một ma trận với một ma trận khác. Hãy cùng xem ví dụ dưới đây.
Chúng ta có thể định nghĩa phép nhân ma trận với một đại lượng vô hướng về mặt toán học là:
Nếu A = [a ij ] m × n là một ma trận và k là một vô hướng, thì kA là một ma trận khác thu được bằng cách nhân từng phần tử của A với k vô hướng.
Nói cách khác, kA = k [a ij ] m × n = [k (a ij )] m × n , nghĩa là, phần tử thứ (i, j) của kA là ka ij với tất cả các giá trị có thể có của i và j.
Ví dụ: Nhân ma trậnA = [3049- 15] bằng 4.
Giải pháp:
Được,
A = [3049- 15]
4 × A = 4 × [3049- 15]
Bây giờ, chúng ta phải nhân từng phần tử của ma trận A với 4.
= [1201636- 420]
Đây là ma trận bắt buộc sau khi nhân ma trận đã cho với giá trị hằng số hoặc vô hướng, tức là 4.
Điều kiện nhân ma trận
Để thực hiện phép nhân hai ma trận , chúng ta nên đảm bảo rằng số cột trong ma trận thứ nhất bằng số hàng trong ma trận thứ hai. Do đó, sản phẩm của ma trận thu được sẽ có một số hàng của ma trận thứ nhất và một số cột của ma trận thứ hai. Bậc của ma trận kết quả là bậc nhân ma trận .
Bây giờ, chúng ta hãy hiểu cách thực hiện phép nhân ma trận với các thứ tự khác nhau hoặc các loại ma trận khác nhau .
Làm thế nào để Nhân ma trận?
Chúng ta hãy học cách nhân ma trận.
Xét ma trận A là ma trận a × b và ma trận B là ma trận ab × c.
Khi đó, ma trận C = AB được định nghĩa là ma trận A × B.
Một phần tử trong ma trận C, C xy được xác định là C xy = A x1 B y1 +… .. + A xb B bởi = ∑bk = 1 A xk B ky cho x = 1 …… a và y = 1 …… .c
Đây là một trong những chuyên đề quan trọng nhất lớp 12. Bài giải ma trận lớp 12 giải chi tiết các dạng của ma trận.
Ký hiệu
Nếu A là ma trận am × n và B là ma trận ap × q, thì tích ma trận của A và B được biểu diễn bằng:
X = AB
Trong đó X là ma trận kết quả có kích thước m × q.
Công thức nhân ma trận
Hãy lấy một ví dụ để hiểu công thức này.
Giả sử A và B là hai ma trận, sao cho
A =⎡⎣⎢⎢⎢A11A21Am 1A12A22… … … … .Am 2⋯⋯⋯A1 nA2 nAm n⎤⎦⎥⎥⎥, B =⎡⎣⎢⎢⎢B11B21Bm 1B12B22… … … … .Bm 2⋯⋯⋯B1 nB2 nBm n⎤⎦⎥⎥⎥Khi đó Ma trận C = AB được ký hiệu là
C = ⎡⎣⎢⎢⎢C11C12… … .C1 cC21C22… … .C2 c… … … … …Cmột 1Cmột 2… … .Cmột c⎤⎦⎥⎥⎥
Một phần tử trong ma trận C trong đó C là phép nhân của Ma trận AX B.
C = C xy = A x1 B y1 +… .. + A xb B bởi = ∑bk = 1 A xk B ky cho x = 1 …… a và y = 1 …… .c
Thuật toán cho phép nhân ma trận
Trong những năm gần đây đã có rất nhiều công trình nghiên cứu trong lĩnh vực thuật toán nhân ma trận vì nó đã được tìm thấy ứng dụng của nó trong nhiều lĩnh vực. Có bốn loại thuật toán:
- Thuật toán lặp lại
- Thuật toán phân chia và chinh phục
- Thuật toán khối con
- Thuật toán song song và phân tán
Điều này chủ yếu được sử dụng trong các ngôn ngữ lập trình khác nhau như C, Java, v.v., để nhân trực tuyến. Phổ biến nhất là 2 × 2, 3 × 3 và 4 × 4, phép nhân ma trận.
Phép toán là nhị phân với các mục trong một tập hợp các phép toán cộng, trừ, nhân và chia được xác định. Các phép toán này giống như các phép toán tương ứng trên số thực và số hữu tỉ.
Mặc dù có nhiều ứng dụng của ma trận nhưng về cơ bản, phép nhân ma trận là một phép toán trong đại số tuyến tính. Ánh xạ tuyến tính, bao gồm phép cộng và phép nhân vô hướng, được biểu diễn bằng phép nhân ma trận.
Người ta cũng có thể tìm thấy một loạt các thuật toán trên các mắt lưới. Loại thuật toán này được thiết kế để giảm thiểu tính kém hiệu quả vốn có của các thuật toán mảng tiêu chuẩn, nơi có thể có độ trễ khi dữ liệu đến từ 2 ma trận khác nhau.
Quy tắc nhân ma trận
Từ công thức và quy trình đã xác định ở trên, chúng ta có thể viết các quy tắc và tính chất sau cho phép nhân ma trận.
- Tích của hai ma trận A và B được xác định nếu số cột của A bằng số hàng của B.
- Nếu AB được xác định, thì BA không cần được xác định
- Nếu cả A và B đều là ma trận vuông cùng bậc thì cả AB và BA đều được xác định.
- Nếu AB và BA đều xác định thì không cần AB = BA.
- Nếu tích của hai ma trận là ma trận 0, thì không nhất thiết một trong hai ma trận là ma trận 0.
Phép nhân ma trận 2 × 2
Hãy xem xét một phép nhân ma trận 2 × 2 đơn giản A = [3479] và một ma trận khác B = [652số 8]
Bây giờ mỗi phần tử của ma trận tích AB có thể được tính như sau:
- AB 11 = 3 × 6 + 7 × 5 = 53
- AB 12 = 3 x 2 + 7 x 8 = 62
- AB 21 = 4 × 6 + 9 × 5 = 69
- AB 22 = 4 x 2 + 9 x 8 = 80
Do đó ma trận AB = [53696280]
Phép nhân ma trận 3 × 3
Để hiểu phép nhân hai ma trận 3 × 3, chúng ta hãy xét hai ma trận 3 × 3 A và B.
Ma trận A = ⎡⎣⎢1239số 817số 841410⎤⎦⎥, Ma trận B = ⎡⎣⎢5671915số 83916⎤⎦⎥
Mỗi phần tử của ma trận sản phẩm AB có thể được tính như sau:
- AB 11 = 12 × 5 + 8 × 6 + 4 × 7 = 136
- AB 12 = 12 x 19 + 8 x 15 + 4 x 8 = 380
- AB 13 = 12 x 3 + 8 x 9 + 4 x 16 = 172
- AB 21 = 3 × 5 + 17 × 6 + 14 × 7 = 215
- AB 22 = 3 x 19 + 17 x 15 + 14 x 8 = 424
- AB 23 = 3 x 3 + 17 x 9 + 14 x 16 = 386
- AB 31 = 9 x 5 + 8 x 6 + 10 x 7 = 163
- AB 32 = 9 x 19 + 8 x 15 + 10 x 8 = 371
- AB 33 = 9 x 3 + 8 x 9 + 10 x 16 = 259
Do đó, ma trận AB = ⎡⎣⎢136215163380424371172386259⎤⎦⎥
Các thuộc tính của phép nhân ma trận
Sau đây là các tính chất của phép nhân ma trận:
Tính chất giao hoán
Phép nhân ma trận không có tính chất giao hoán.
Giả sử rằng, nếu A và B là hai ma trận 2 × 2,
AB ≠ BA
Trong phép nhân ma trận, thứ tự quan trọng rất nhiều.
Ví dụ,
Nếu A = [1324] và B = [3124] là hai ma trận, sau đó
A × B = [1324] × [3124]
A × B = [5131022]
Nhưng,
B × A = [3124] × [1324]
B × A = [9131418]
Điều này cho thấy ma trận AB ≠ BA.
Do đó, phép nhân hai ma trận không có tính chất giao hoán.
Bất động sản kết hợp
Nếu A, B và C là ba ma trận, thì thuộc tính kết hợp của phép nhân ma trận cho biết rằng,
(AB) C = A (BC)
Để cho A = [1121]
B = [3122]
C= [0213]
LHS = (AB) C
A × B = [1121] × [3122]
A × B = [5464]
( A B ) C= [5464] × [0213]
( A B ) C= [12số 82316]
RHS = A (BC)
B C= [3122] × [0213]
B C= [4497]
A ( B C) = [1121] × [4497]
A ( B C) = [12số 82316]
Do đó, tính chất kết hợp của phép nhân ma trận được chứng minh.
Thuộc tính phân tán
Nếu A, B và C là ba ma trận, thuộc tính phân phối của phép nhân ma trận nói rằng,
- (B + C) A = BA + CA
- A (B + C) = AB + AC
Thuộc tính nhận dạng đa nhân
Thuộc tính nhận dạng của phép nhân ma trận nói rằng,
- I = I. A = A
Trong đó A là ma trận n × n và “I” là ma trận nhận dạng bậc n.
Để cho A = [2136] và Tôi= [1001]
Một . Tôi= [2136] × [1001]
Một . Tôi= [2136] =A
Thuộc tính thứ nguyên
Trong phép nhân ma trận, tích của ma trận m × n và n × a là ma trận m × a.
Ví dụ, ma trận A là ma trận 2 × 3 và ma trận B là ma trận 3 × 4, thì AB là ma trận 2 × 4.
Thuộc tính nhân của số không
Nếu một ma trận được nhân với ma trận không, thì ma trận kết quả là ma trận không.
Nếu A = [2112] được nhân với ma trận 0 (tức là,)[0000], sản phẩm trở thành [0000]
Ví dụ đã giải quyết
Phép nhân ma trận 4 × 4 được giải thích dưới đây với hai ma trận 4 × 4 A và B.
A = ⎡⎣⎢⎢⎢74141314số 82171512666394⎤⎦⎥⎥⎥, B = ⎡⎣⎢⎢⎢5số 813671663144số 822944⎤⎦⎥⎥⎥
Thực hiện các bước tương tự như trong 2 ví dụ trước, chúng ta có thể xây dựng một ma trận AB.
AB = ⎡⎣⎢⎢⎢378258370223381237497251286190346266224140277129⎤⎦⎥⎥⎥
Các vấn đề thực hành về phép nhân ma trận
Giải quyết các vấn đề sau:
- Tìm sản phẩm: 3 [7251]
- Đơn giản hóa ma trận 3 × 3 sau: ⎡⎣⎢121631215⎤⎦⎥×⎡⎣⎢142số 826731⎤⎦⎥
- Tìm tích của AB, nếu A = [5931] và B = [16012]
- Tìm tích của ma trận, nếu A =⎡⎣⎢421⎤⎦⎥ và [246]
- Tính toán: – 47⎡⎣⎢- 224935⎤⎦⎥
Tìm hiểu thêm về Ma trận và các chủ đề liên quan khác một cách vui vẻ và thú vị. Tải xuống BYJU’S – Ứng dụng Học tập ngay hôm nay.
Câu hỏi thường gặp – Câu hỏi thường gặp
Phép nhân ma trận là gì?
Phép nhân ma trận là một phương pháp tìm tích của hai ma trận để nhận được kết quả là một ma trận. Nó là một loại hoạt động nhị phân.
Làm thế nào để nhân hai ma trận đã cho?
Để nhân ma trận này với ma trận khác, trước hết chúng ta cần kiểm tra xem số cột của ma trận thứ nhất có bằng số hàng của ma trận thứ hai hay không. Bây giờ nhân từng phần tử của cột của ma trận đầu tiên với từng phần tử của các hàng của ma trận thứ hai và cộng tất cả chúng. Chúng ta cần thực hiện sản phẩm dấu chấm của các cột và hàng ở đây.
Kết quả của phép nhân ma trận (2 × 3) và (3 × 3) là gì?
Kết quả của phép nhân ma trận (2 × 3) và (3 × 3) sẽ chỉ là ma trận 2 × 3.
Cách nhân 3 × ma trận 3 3?
Nhân mỗi hàng của ma trận đầu tiên với mỗi col umn của ma trận econd s và cộng tất cả để có phần tử đầu tiên. Tương tự, nhân và cộng các phần tử của hai ma trận, theo cột và theo hàng, để được các phần tử của produ ct của hai ma trận 3 × 3.
Làm thế nào để tìm phép nhân của hai ma trận?
Nếu A là ma trận am × n và B là ma trận ap × q, thì phép nhân của A và B được ký hiệu là ma trận điểm, chẳng hạn như:C = ABNhư vậy, C sẽ là ma trận m × q.
MA TRẬN-ĐỊNH THỨC-HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Phép nhân hai ma trận
Báo cáo vấn đề
Trong bài toán “Nhân hai ma trận”, chúng ta đã đưa ra hai ma trận. Chúng ta phải nhân các ma trận này và in ra kết quả hoặc kết quả cuối cùng ma trận. Ở đây, điều kiện cần và đủ là số cột trong A phải bằng số hàng trong ma trận B. Nếu điều kiện này không đúng thì chúng ta không thể nhân các ma trận này được.
Định dạng đầu vào
Dòng đầu tiên chứa bốn giá trị nguyên r1, c1, r2, c2. Trong đó r1 và c1 biểu thị số hàng và cột của ma trận đầu tiên. Và r2, c2 biểu thị số hàng, số cột của ma trận thứ hai.
R1 dòng tiếp theo chứa c1 giá trị nguyên.
Và r2 dòng tiếp theo chứa các giá trị nguyên c2.
Định dạng đầu ra
In ma trận cuối cùng sau khi nhân theo cách như vậy mọi hàng bắt đầu từ dòng mới và mọi phần tử cách nhau bởi dấu cách trong mỗi hàng.
Những ràng buộc
- 1 <= r1, c1, r2, c2 <= 2000.
- 1 <= | m [i] [j] | <= 10 ^ 9 trong đó m là ma trận và vị trí của phần tử ở hàng thứ i và cột thứ j.
Ví dụ

Giải thích: Trong ví dụ trên, chúng ta có phần tử đầu tiên ở đầu ra bằng cách nhân tất cả các phần tử tương ứng trong hàng đầu tiên của ma trận A với các phần tử trong cột đầu tiên của ma trận B và cộng chúng. Tương tự, đối với phần tử thứ hai trong hàng đầu tiên của đầu ra, chúng ta cần lấy hàng đầu tiên của ma trận A và cột thứ hai của ma trận B. Bằng cách này, chúng tôi nhận được tất cả các phần tử trong ma trận đầu ra.
Dưới đây là ví dụ ngẫu nhiên cho phép nhân ma trận.
Thuật toán nhân hai ma trận
1. Đơn giản chỉ cần chạy ba vòng.2. Vòng lặp cho mỗi hàng trong ma trận A với biến i.3. Bên trong vòng lặp trên, Vòng lặp cho mỗi cột trong ma trận B với biến j.4. Bên trong hai vòng lặp trên, Vòng lặp cho mỗi phần tử hàng trong ma trận A với biến k và mỗi phần tử cột trong ma trận B với biến k tức là, A [i] [k] và B [k] [j].5. chúng ta sẽ tìm tích của mỗi phần tử hàng trong A với mỗi phần tử cột trong B. tức là, A [i] [k] * B [k] [j] và thêm tất cả các sản phẩm và lưu trữ trong ma trận C mới, tức là, C [i] [j].6. ma trận C là đầu ra của phép nhân.
Thực hiện
Chương trình C ++ cho phép nhân hai ma trận
Code
Hướng dẫn nhân hai ma trận với nhau bằng máy tính Casio fx570ES PLUS
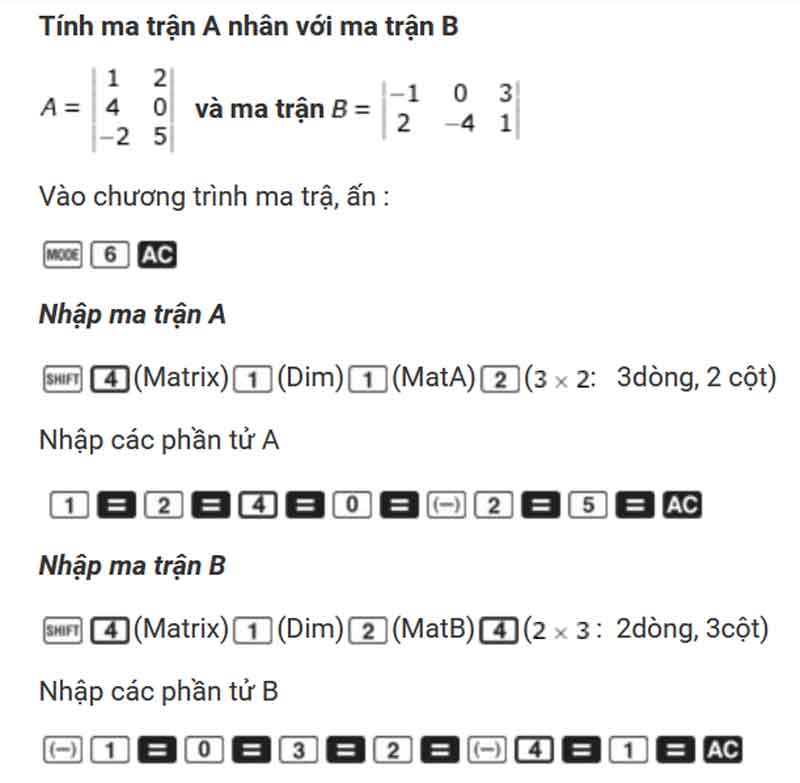
Tính A ma trận A nhân với B

✅ Phương pháp học ⭐️⭐️⭐️⭐️⭐️
🎓 GIA SƯ TOÁN CAO CẤP