Trong bài viết dưới đây, điện máy Sharp Việt Nam sẽ hướng dẫn cách viết phương trình Parabol dạng tổng quát và chính tắc, cách xác định tọa độ đỉnh của parabol hay sự tương giao giữa đường thẳng và Parabol kèm theo ví dụ minh họa chi tiết để các bạn cùng tham khảo
Parabol là gì?
parabol là một đường conic được tạo bởi giao của một hình nón và một mặt phẳng song song với đường sinh của hình đó. Một parabol cũng có thế được định nghĩa như một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
Ví dụ: Cho một điểm F cố định và một đường thẳng Δ cố định không đi qua F. Thì đường Parabol là tập hợp tất cả các điểm M cách đều F và Δ. Trong đó:
- Điểm F được coi là tiêu điểm của Parabol
- Đường thẳng Δ được gọi là đường chuẩn của parabol.
- Khoảng cách từ F đến Δ được gọi là tham số tiêu của parabol.
Phương trình Parabol
1. Phương trình tổng quát của Parabol
Dạng tổng quát của phương trình Parabol có dạng: y = a2 + bx + c
- Hoành độ của đỉnh là −b/2a
- Thay tọa độ trục hoành vào phương trình, ta tìm được hoành độ Parabol có công thức dưới dạng: (b2−4ac)/4a.
- Tọa độ đỉnh của Parabol và hình dạng phụ thuộc vào dấu của a
2. Phương trình chính tắc của Parabol
Phương trình chính tắc của parabol được biểu diễn dưới dạng: y2 = 2px (p > 0)
Chứng minh:
Cho parabol với tiêu điểm F và đường chuẩn Δ.
Kẻ FP⊥Δ (P∈Δ). Đặt FP = p.
Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của FP và điểm F nằm trên tia Ox.
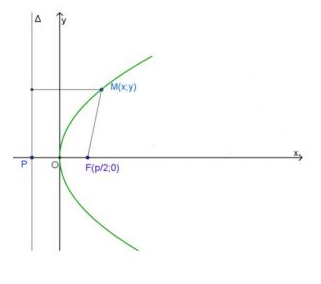
Suy ra ta có F = (P/2; 0), P = (−P/2; 0)
Và phương trình của đường thẳng Δ là x + p2 = 0
Điểm M(x ; y) nằm trên parabol đã cho khi và chỉ khi khoảng cách MF bằng khoảng cách từ M tới Δ, tức là:
√(x-p/2)2 + y2 = |x + p/2|
Bình phương 2 vế của đẳng thức rồi rút gọn, ta được phương trình chính tắc của parabol:
y2 = 2px (p > 0)
Chú ý: Ở môn đại số, chúng ta gọi đồ thị của hàm số bậc hai y = ax2 + bx + c là một đường parabol.
3. Cách vẽ Parabol
Cho hàm số y = ax2. Hàm số này xác định trên R :
- Nếu a > 0 thì hàm số giảm trên (-∞ ; 0) ; tăng trên (0;+ ∞ ),đạt cực tiểu khi x = 0
- Nếu a < 0 thì hàm số tăng trên (-∞ 0) ;giảm trên (0;+ ∞ ).đạt cực đại khi x = 0
Đồ thị Parabol của hàm số y = ax2 có đỉnh là gốc O và trục đối xứng là Oy.
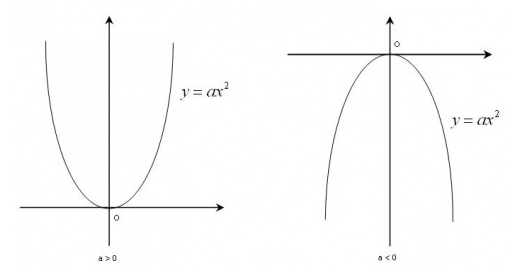
Tọa độ đỉnh Parabol là điểm O (0;0)
Tham khảo thêm:
- Viết phương trình đường thẳng đi qua hai điểm có VD từ A – Z
- Phương trình mặt cầu và các dạng bài tập có lời giải từ A – Z
- Khoảng cách từ điểm đến mặt phẳng trong không gian chuẩn 100%
Cách viết phương trình Parabol
Bước 1: Giả sử Parabol (P): y= ax2 + bx + c, với a ≠ 0.
Bước 2: Dựa vào điều kiện K để xác định a, b, c.
Trong bước này ta cần lưu ý các điều kiện thường gặp sau: Điểm A(x0, y0) ∈ (P) ta nhận được điều kiện: y0 = ax02 + bx0 + c.

Bước 3: Kết luận.
Ví dụ 1:Viết phương trình Parapol (P) có đỉnh là góc tọa độ và đi qua điểm A (2,2)
Parapol (P) có đỉnh O có phương trình (P): y2 = 2px hoặc (P): x2 = 1py
Trường hợp 1: Nếu phương trình của (P): y2 = 2px
Vì A ∈ (P), suy ra 4 = 4p ⇔ p =1
Khi đó phương trình Parapol của (P1): y2 = 2x
Trường hợp 2: Nếu phương trình của (P): x2 = 1py
Vì A ∈ (P), suy ra 4 = 4p ⇔ p =1
Khi đó phương trình Parapol của (P1): x2 = 2y
Vậy tồn tại hai Parabol (P1) và (P2) thỏa mã điều kiện của đề bài
Ví dụ 2: Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó:
a. Đi qua hai điểm M(1; 5) và N(-2; 8). b. Đi qua điểm A(3; -4) và có trục đối xứng là x = -3/2. c. Có đỉnh là I(2; -2). d. Đi qua điểm B(-1; 6) và tung độ của đỉnh là -1/4.
Lời giải
a. Ta có:
M(1; 5) ∈ (P) ⇔ 5 = a + b + 2 (1)
N(-2; 8) ∈ (P) ⇔ 8 = 4a – 2b + 2 (2)
Giải hệ phương trình tạo bởi (1) và (2) ta được a = 2 và b = 1.
Vậy, ta được (P): y = 2×2 + x + 2.
b. Ta có: A(3; -4) ∈ (P) ⇔ -4 = 9a + 3b + 2 (1)
Trục đối xứng x = -3/2 ⇔ -b/2a= -3/2 ⇔ b = 3a (2)
Giải hệ phương trình tạo bởi (1) và (2) ta được a = – 1/3 và b = -1.
Vậy, ta được (P): y = – 1/3×2 – x + 2.
c. Ta có:Đỉnh I(2; -2). Mà đỉnh S(−b/2a;−Δ/4a) nên −b/2a = 2 (1)
I(2, -2) ∈ (P) ⇔ -2 = 4a + 2b + 2 ⇔ 2a + b = -2 (2)
Giải hệ phương trình tạo bởi (1) và (2) ta được a = 1 và b = -4.
Vậy, ta được (P): y = x2 – 4x + 2.
d. Ta có: B(-1; 6) ∈ (P) ⇔ 4 = a – b (1)
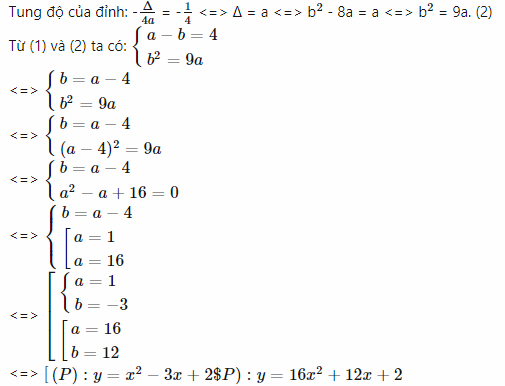
Vậy, có hai parabol thoả mãn đề bài.
Cách xác định tọa độ đỉnh của parabol
Ví dụ: Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.
a) y = x2 – 3x + 2
b)y = −2×2 + 4x – 3
Hướng dẫn:
a) y = x2- 3x + 2. Có hệ số: a = 1, b = – 3, c = 2.
Δ = b2 – 4ac = (-3)2 – 4.1.2 = – 1
Tọa độ đỉnh của đồ thị hàm số I(−b/2c;−Δ/4a)
- Hoành độ đỉnh xI = −b/2a = −3/2
- Tung độ đỉnh yI = −Δ/4a = −1/4
Vậy đỉnh parabol là I(−3/2; −1/4)
Cho x = 0 → y = 2 ⇒ A(0; 2) là giao điểm của đồ thị hàm số với trục tung.
Cho y = 0 ↔ x2-3x+2=0 ⇔ x1 = 1 và x2 = 2
Suy ra B(1; 0) và C(2; 0) là giao điểm của đồ thị hàm số với trục hoành.
b) Cho y = −2×2 + 4x – 3. Có a = -2 , b = 4, c = -3
Δ = b2 – 4ac = 42 – 4. (-2).(-3) = – 8
Tọa độ đỉnh của đồ thị hàm số I(−b/2c;−Δ/4a)
- Hoành độ đỉnh xI = −b/2a = 1
- Tung độ đỉnh yI = −Δ/4a = 1
Vậy đỉnh parabol là I (1; 1)
Cho x = 0 => y = – 3 ⇒ A(0; -3) là giao điểm của đồ thị hàm số với trục tung.
Cho y = 0 => -2×2 + 4x – 3 = 0
Δ = b2 – 4ac = 42 – 4. (-2).(-3) = – 8 < 0.
Phương trình vô nghiệm ⇒ không tồn tại giao điểm của hàm số với trục hoành.
Sự tương giao giữa đường thẳng và Parabol
Sự tương giao giữa đường thẳng d: y = mx + n và parabol (P): y = ax2(a≠0).
Số giao điểm của đường thẳng d và parabol (P) là số nghiệm của phương trình hoành độ giao điểm
ax2 = mx + n ⇔ ax2 − mx −n = 0(*)
- Phương trình (*) có hai nghiệm phân biệt (Δ > 0) thì d cắt (P) tại hai điểm phân biệt
- Phương trình (*) có nghiệm kép (Δ = 0) thì d tiếp xúc với (P).
- Phương trình (*) vô nghiệm (Δ < 0) thìdkhông cắt (P)
Ví dụ :Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
a, Xác định tọa độ giao điểm của parabol và đường thẳng khi m = 6
b, Biện luận theo m số giao điểm của đường thẳng và parabol
Lời giải:
a, Với m = 6, ta có (d): y = x + 6
Phương trình hoành độ giao điểm giữa parabol (P) và đường thẳng (d) là:
x2 = x + 6 ⇔ x2 – x – 6 = 0 (1)
Ta có Δ = b2 – 4ac = 1 – 4.(-6) = 25 > 0
Phương trình (1) có hai nghiệm phân biệt
Với x = 3 ta có y = 9
Với x = -2 ta có y = 4
Vậy với m = 6 thì parabol (P) cắt đường thẳng (d) tại hai điểm có tọa độ A(3; 9) và B(-2; 4)
b, Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d): x2 = x + m ⇔ x2 – x – m = 0 (1)
Ta có Δ = b2 – 4ac = 1 – 4.(-m) = 1 + 4m
Nếu Δ > 0 ⇔ 1 + 4m > 0 ⇔ m > -1/4 thì phương trình (1) có hai nghiệm phân biệt hai parabol (P) cắt đường thẳng (d) tại hai điểm phân biệt
Nếu Δ < 0 ⇔ 1 + 4m < 0 ⇔ m < -1/4 thì phương trình (1) vô nghiệm hay parabol (P) và đường thẳng (d) không có điểm chung
Nếu Δ = 0 ⇔ 1 + 4m = 0 ⇔ m = -1/4 thì phương trình (1) có nghiệm kép hay parabol (P) tiếp xúc với đường thẳng (d) tại một điểm
Hy vọng với những kiến thức mà chúng tôi vừa chia sẻ có thể giúp các bạn biết cách viết phương trình Parabol tổng quát, chính tắc và cách xác định tọa độ đỉnh của parabol để ứng dụng vào làm bài tập nhé