Bài viết này chúng ta cùng hệ thống lại cách giải một số dạng bài tập về hàm số, đồ thị hàm số y=ax để các em hiểu rõ hơn và dễ dàng vận dụng giải các bài toán tương tự khi gặp. Nhưng trước tiên chúng ta cùng tóm tắt lại phần lý thuyết của hàm số, đồ thị hàm số:
I. Lý thuyết về hàm số, đồ thị hàm số
• Nếu đại lượng y phụ thuộc vào đại lượng x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
• Lưu ý: Nếu x thay đổi mà y không thay đổi thì y được gọi là hàm số hằng (hàm hằng).
• Với mọi x1; x2 ∈ R và x1<x2 mà f(x1)<f(x2) thì hàm số y = f(x) được gọi làm hàm đồng biến.
• Với mọi x1; x2 ∈ R và x1<x2 mà f(x1)>f(x2) thì hàm số y = f(x) được gọi làm hàm nghịch biến.
• Hàm số y = ax (a ≠ 0) được gọi là đồng biến trên R nếu a > 0 và nghịch biến trên R nếu a < 0.
• Tập hợp tất cả các điểm (x, y) thỏa mãn hệ thức y = f(x) thì được gọi là đồ thị của hàm số y = f(x).
• Đồ thị hàm số y = f(x) = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ và điểm (1; a).
II. Các dạng bài tập về hàm số và đồ thị hàm số
° Dạng 1: Xác định đại lượng y có phải là hàm số của đại lượng x không.
* Phương pháp giải:
– Kiểm tra điều kiện: Mỗi giá trị của x được tương ứng với 1 và chỉ 1 giá trị của y.
* Ví dụ 1 (bài 24 trang 63 SGK Toán 7 tập 1): Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:
x -4 -3 -2 -1 1 2 3 4 y 16 9 4 1 1 4 9 16
– Đại lượng y có phải là hàm số của đại lượng x không?
* Lời giải ví dụ 1 (bài 24 trang 63 SGK Toán 7 tập 1):
– Vì với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.
* Ví dụ 2 (bài 27 trang 64 SGK Toán 7 tập 1): Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là
a)
x -3 -2 -1 1/2 1 2 y -5 -7,5 -15 30 15 7,5
b)
x 0 1 2 3 4 y 2 2 2 2 2
* Lời giải ví dụ 2 (bài 27 trang 64 SGK Toán 7 tập 1):
a) Vì với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x;
b) Vì với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng, trong trường hợp này với mọi x thì y luôn nhận duy nhất một giá trị là 2 nên đây là một hàm hằng.
° Dạng 2: Tính giá trị của hàm số khi biết giá trị của biến.
* Phương pháp giải:
– Nếu hàm số cho bằng bảng thì cặp giá trị tương ứng của x và y nằm cùng 1 cột.
– Nếu hàm số cho bằng công thức, ta thay giá trị của biến đã cho vào công thức để tính giá trị tương ứng của hàm số
* Ví dụ 1 (bài 25 trang 64 SGK Toán 7 tập 1): Cho hàm số y = f(x) = 3×2 + 1. Tính: f(1/2); f(1); f(3).
* Lời giải ví dụ 1 (bài 25 trang 64 SGK Toán 7 tập 1):
– Ta có: y = f(x) = 3×2 + 1. nên:
* Ví dụ 2 (bài 26 trang 64 SGK Toán 7 tập 1): Cho hàm số y = 5x – 1. Lập bảng các giá trị tương ứng của y khi: x = -5; -4; -3; -2; 0; 1/5.
* Lời giải ví dụ 2 (bài 26 trang 64 SGK Toán 7 tập 1):
– Ta có: y = 5x – 1 nên:
Khi x = -5 ⇒ y = 5.(-5) – 1 = -25 – 1 = -26
Khi x = -4 ⇒ y = 5.(-4) – 1 = -20 – 1 = -21
Khi x = -3 ⇒ y = 5.(-3) – 1 = -15 – 1 = -16
Khi x = -2 ⇒ y = 5.(-2) – 1 = -10 – 1 = -11
Khi x = 0 ⇒ y = 5.(0) – 1 = 0 – 1 = -1
Khi x = 1/5 ⇒ y = 5.(1/5) – 1 = 1 – 1 = 0.
– Như vậy ta có bảng giá trị tương ứng sau:
x -5 -4 -3 -2 0 1/5 y -26 -21 -16 -11 -1 0
* Ví dụ 3 (bài 28 trang 64 SGK Toán 7 tập 1): Cho hàm số y = f(x) = 12/x
a) f(5) = ?; f(-3) = ?
b) Hãy điền các giá trị tương ứng của hàm số vào bảng sau:
x -6 -4 -3 2 5 6 12 f(x)=12/x
* Lời giải ví dụ 3 (bài 28 trang 64 SGK Toán 7 tập 1):
– Ta có: y = f(x) = 12/x nên:
a) ;
b) Ta có: khi x = – 6 ⇒
– Tương tự, lần lượt thay các giá trị còn lại của x là: x = -4 ; -3 ; 2 ; 5 ; 6 ; 12 vào công thức hàm số: y = 12/x ta được các giá trị y tương ứng là:-3; -4; 6; 2,4; 2; 1 và ta có được bảng sau:
x -6 -4 -3 2 5 6 12 f(x)=12/x -2 -3 -4 6 2,4 2 1
* Ví dụ 4 (bài 29 trang 64 SGK Toán 7 tập 1): Cho hàm số y = f(x) = x2 – 2. Hãy tính f(2) ; f(1) ; f(0) ; f(-1) ; f(-2)
* Lời giải ví dụ 4 (bài 29 trang 64 SGK Toán 7 tập 1):
– Ta có y= f(x) = x2 – 2 nên:
f(2) = 22 – 2 = 4 – 2 = 2
f(1) = 12 – 2 = 1 – 2 = -1
f(0) = 02 – 2 = 0 – 2 = -2
f(-1) = (-1)2 – 2 = 1 – 2 = -1
f(-2) = (-2)2 – 2 = 4 – 2 = 2
* Ví dụ 5 (bài 30 trang 64 SGK Toán 7 Tập 1): Cho hàm số y = f(x) = 1 – 8x. Khẳng định nào sau đây là đúng
a) f(-1) = 9
b) f(-1/2) = -3
c) f(3) = 25
* Lời giải ví dụ 5 (bài 30 trang 64 SGK Toán 7 Tập 1):
– Ta có y = f(x) = 1 – 8x.
a) Vậy f(-1) = 1 – 8(-1) = 1 + 8 = 9 ⇒ khẳng định a) ĐÚNG.
b) f(1/2) = 1 – 8(1/2) = 1 – 4 = -3 ⇒ khẳng định b) ĐÚNG
c) f(3) = 1 – 8.3 = 1 – 24 = -23 ⇒ khẳng định c) SAI
* Ví dụ 6 (bài 31 trang 65 SGK Toán 7 Tập 1): Cho hàm số y=(2/3)x. Điền số thích hợp vào ô trống trong bảng sau:
x -0,5 4,5 9 y -2 0
* Lời giải ví dụ 6 (bài 31 trang 65 SGK Toán 7 Tập 1):
– Ta có: nên:
khi x = -0,5 ⇒
khi y = -2 ⇒
Khi y = 0 ⇒
Khi x = 4,5 ⇒
Khi x = 9 ⇒
– Như vậy ta được bảng sau:
x -0,5 -3 0 4,5 9 y -1/3 -2 0 3 6
° Dạng 3: Tìm tọa độ một điểm và vẽ 1 điểm khi biết tọa độ. Tìm các điểm trên một đồ thị hàm số, biểu diễn và tính diện tích.
* Phương pháp giải:
– Muốn tìm tọa độ một điểm ta vẽ 2 đường thẳng vuông góc với hai trục tọa độ.
– Để tìm một điểm trên một đồ thị hàm số ta cho bất kì 1 giá trị của x rồi tính giá trị y tương ứng.
– Có thể tính diện tích trực tiếp hoặc tính gián tiếp qua hình chữ nhật.
– Chú ý: Một điểm thuộc Ox thì tung độ bằng 0, thuộc trục Oy thì hoành độ bằng 0.
* Ví dụ 1 (bài 33 trang 67 SGK Toán 7 Tập 1): Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm: A(3;-1/2); B(-4;2/4); C(0;2,5)
* Lời giải ví dụ 1 (bài 33 trang 67 SGK Toán 7 Tập 1):
– Cặp số (x0;y0) gọi là tọa độ của một điểm M với x0 là hoành độ và y0 là tung độ của điểm M.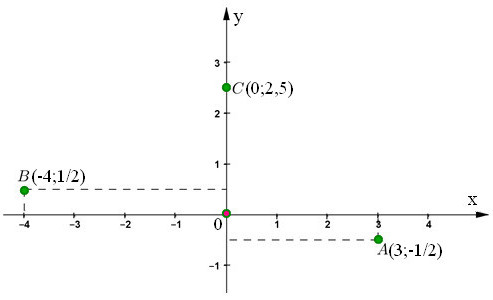
* Ví dụ 2 (bài 32 trang 67 SGK Toán 7 Tập 1):
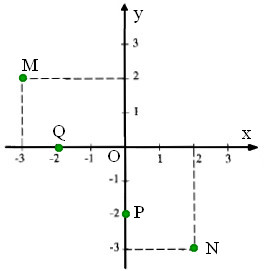
a) Viết tọa độ các điểm M, N, P, Q trong hình dưới (hình 19 trang 67 sgk).
b) Em có nhận xét gì về tọa độ của các cặp điểm M và N, P và Q.
* Lời giải ví dụ 2 (bài 32 trang 67 SGK Toán 7 Tập 1):
a) Từ vị trí các điểm trên hệ trục tọa độ Oxy ta có:
M(-3; 2) ; N(2; -3) ; P(0; -2) ; Q(-2; 0)
b) Nhận xét: Trong mỗi cặp điểm M và N ; P và Q hoành độ của điểm này bằng tung độ của điểm kia và ngược lại
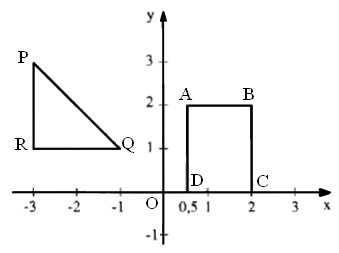
* Ví dụ 3 (bài 35 trang 68 SGK Toán 7 Tập 1): Tìm tọa độ các đỉnh của hình chữ nhật ABCD và của hình tam giác PQR trong hình sau (hình 20 sgk).
* Lời giải ví dụ 3 (bài 35 trang 68 SGK Toán 7 Tập 1):
– Dựa vào hệ trục tọa độ Oxy theo bài ra ta có:
A(0,5; 2) ; B(2; 2) ; C(2; 0) ; D(0,5; 0).
P(-3; 3) ; Q(-1; 1) ; R(-3; 1).
* Ví dụ 4 (bài 36 trang 68 SGK Toán 7 Tập 1): Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm A(-4;-1); B (-2;-1); C(-2;-3) ; D(-4;-3). Tứ giác ABCD là hình gì?
* Lời giải ví dụ 4 (bài 35 trang 68 SGK Toán 7 Tập 1):
– Ta vẽ trục tọa độ Oxy và biểu diễn các điểm như hình sau: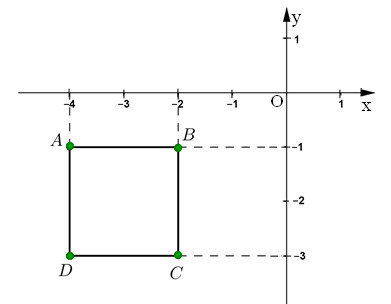
– Từ vị trí các điểm dựng được, ta thấy tứ giác ABCD là hình vuông.
° Dạng 4: Kiểm tra điểm M(x0; y0) có thuộc đồ thị hàm số hay không?
* Phương pháp giải:
– Điểm M(x0; y0) thuộc đồ thị hàm số, nếu ta thay giá trị của x0 và y0 vào hàm số ta được đẳng thức đúng; Ngược lại, nếu đẳng thức sai thì điểm M không thuộc đồ thì hàm số đã cho.
* Ví dụ 1 (bài 41 trang 72 SGK Toán 7 Tập 1): Những điểm nào sau đây thuộc đồ thị của hàm số y = -3x.
A(-1/3; 1); B(-1/3; -1); C(0; 0).
* Lời giải ví dụ 1 (bài 41 trang 72 SGK Toán 7 Tập 1):
– Theo bài ra, y = -3x, ta có:
– Với điểm A(-1/3; 1) thay x = -1/3 và y = 1 vào hàm số nên A thuộc đồ thị hàm số đã cho.
– Tương tự, với B(-1/3; -1) ta được: nên B không thuộc đồ thị hàm số đã cho.
– Với C(0; 0). ta được: 0 = (-3).0 nên C thuộc đồ thị hàm số đã cho.
° Dạng 5: Tìm hệ số a của đồ thị hàm số y = ax biết đồ thị đi qua 1 điểm.
* Phương pháp giải:
– Ta thay tọa độ điểm đi qua vào đồ thị để tìm a.
* Ví dụ 1 (bài 42 trang 72 SGK Toán 7 Tập 1): Đường thẳng OA trong hình 26 là đồ thị của hàm số y = ax.
a) Hãy xác định hệ số a
b) Đánh dấu điểm trên đồ thị có hoành độ bằng 1/2
c) Đánh dấu điểm trên đồ thị có tung độ bằng -1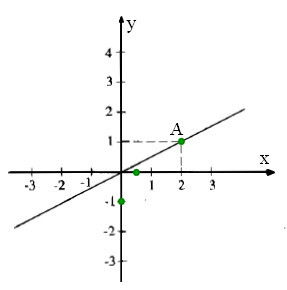
* Lời giải ví dụ 1 (bài 42 trang 72 SGK Toán 7 Tập 1):
a) Ta có A(2; 1) thuộc đồ thị hàm số y = ax nên tọa độ điểm A thỏa mãn hàm y = ax. Tức là 1 = a.2 ⇒ a =1/2.
b) Điểm trên đồ thị có hoành độ bằng 1/2 tức là x=1/2 ⇒
c) Điểm trên đồ thị có tung độ bằng -1, tức là y = -1, từ hàm số
– Ta có hình minh họa sau: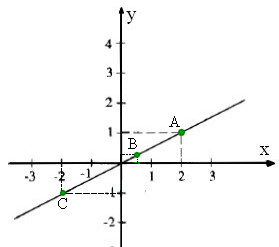
° Dạng 6: Tìm giao điểm của 2 đồ thị y = f(x) và y = g(x)
* Phương pháp giải:
– Cho f(x)=g(x) để tìm x rồi suy ra y và tìm được giao điểm
* Ví dụ 1: Tìm giao điểm của y=2x với y=x+2
* Lời giải:
– Xét hoành độ giao điểm thỏa mãn: 2x = x + 2 ⇒ x = 2 thay giá trị x = 2 vào một trong hai hàm trên ⇒ y = 4.
– Vậy 2 đồ thị giao nhau tại điểm A(2; 4).
° Dạng 7: Chứng minh 3 điểm thẳng hàng
* Phương pháp giải:
– Cách 1: Để chứng minh 3 điểm thẳng hàng, ta lập tỉ số x/y nếu chúng cùng có 1 hệ số tỉ lệ thì suy ra 3 điểm đó cùng thuộc một đồ thị, ngược lại thì 3 điểm không thẳng hàng.
– Cách 2: Viết đồ thị đi qua một điểm rồi thay tạo độ 2 điểm còn lại vào, nếu 2 điểm này đều thỏa đẳng thức thì 3 điểm thẳng hàng, nếu 1 điểm không thỏa thì 3 điểm không thẳng hàng.
* Ví dụ 1: Chứng minh 3 điểm thẳng hàng: A(1;2); B(3;6); C(4;8).
* Lời giải:
– Sử dụng cách 1: Lập tỉ số: nên 3 điểm A,B,C thẳng hàng (cùng nằm trên đồ thị hàm số y=2x).
* Ví dụ 2: Cho A(1;2); B(2,4) C(2a;a+1). Tìm a để 3 điểm A, B, C thẳng hàng.
* Lời giải:
– Cách 1: Để A, B, C thẳng hàng thì:
– Cách 2: Ta có: nên A, B nằm trên đường thẳng y=2x. Để A, B, C thẳng hàng thì C(2a;a+1) phải thuộc hàm y=2x, tức là: a+1 = 2.2a ⇒ a =1/3.
° Dạng 8: Xác định hàm số từ bảng số liệu đã cho, hàm đồng biến hay nghịch biến.
* Phương pháp giải:
– Ta sử dụng kiến thức phần tỉ lệ thuận, tỉ lệ nghịch để tính k rồi biểu diễn y theo x.
– Để xem hàm số đồng biến hay nghịch biến ta dựa vào hệ số a (nếu a>0 hàm đồng biến, a<0 hàm nghịch biến) hoặc giả sử nếu x1>x2 thì hàm đồng biến nếu f(x1)>f(x2) hàm nghịch biến nếu f(x1)<f(x2).
* Ví dụ: Cho bảng số liệu sau, xác định hàm số y theo x và cho biết hàm số đồng biến hay nghịch biến:
x 1 2 3 4 y 2 4 6 8
* Lời giải:
– Ta có: nên y=2x. Vì a=2>0 nên hàm số đồng biến.
° Dạng 9: Tìm điều kiện để 2 đường thẳng cắt nhau, song song, trùng nhau, vuông góc với nhau.
* Phương pháp giải:
• Cho hai đường thẳng y = a1x + b1 và y = a2x + b2:
– Cắt nhau nếu a1 ≠ a2;
– Song song nếu a1 = a2 và b1≠ b2
– Trùng nhau nếu a1 = a2 và b1= b2
– Vuông góc nếu a1.a2 = -1
* Ví dụ: Cho y=(a+1)x-2 và y=2x. Tìm a để hai đường thẳng cắt nhau, song song, trùng nhau.
* Lời giải:
– Hai đường thẳng cắt nhau khi: a1 ≠ a2 ⇒ a+1 ≠ 2, hay a≠1.
– Hai đường thẳng song song khi: a1 = a2 ( vì b1≠b2) ⇒ a+1 = 2, hay a=1.
– Vì b1 = -2 ≠ b2 = 0 nên hai đường thẳng không trùng nhau.
– Hai đường thẳng vuông góc khi a1.a2 = -1 ⇒ (a+1).2 = -1 ⇒ a = -3/2.
III. Một số bài tập luyện tập về hàm số, đồ thị hàm số
* Bài 1: Viết công thức của hàm số y = f(x) biết rằng y tỷ lệ thuận với x theo hệ số tỷ lệ 1/4
a) Tìm x để f(x) = -5.
b) Chứng tỏ rằng nếu x1>x2 thì f(x1)>f(x2)
* Bài 2: Viết công thức của hàm số y = f(x) biết rằng y tỉ lệ nghịch với x theo hệ số a =6.
a) Tìm x để f(x) = 1
b) Tìm x để f(x) = 2
c) Chứng tỏ rằng f(-x) = -f(x).
* Bài 3: Đồ thị hàm số y = ax đi qua điểm A (4; 2)
a) Xác định hệ số a và vẽ đồ thị của hàm số đó.
b) Cho B (-2, -1); C ( 5; 3). Không cần biểu diễn B và C trên mặt phẳng tọa độ, hãy cho biết ba điểm A, B, C có thẳng hàng không?
* Bài 4: Cho hàm số y = (-1/3)x
a) Vẽ đồ thị hàm số
b) Các điểm A(-3; 1); B(6; 2); P(9; -3) điểm nào thuộc đồ thị
* Bài 5: Hàm số f(x) được cho bởi bảng sau:
x -4 -2 -1 y 8 4 2
a) Tính f(-4) và f(-2)
b) Hàm số f được cho bởi công thức nào?
* Bài 6: Cho hàm số y = x.
a) Vẽ đồ thị (d) của hàm số.
b) Gọi M là điểm có tọa độ là (3;3). Điểm M có thuộc (d) không? Vì sao?
c) Qua M kẻ đường thẳng vuông góc với (d) cắt Ox tại A và Oy tại B. Tam giác OAB là tam giác gì? Vì sao?
* Bài 7: Hàm số y = ax được cho bởi bảng sau:
x 1 3 -2 y 3 9 6
a) Tìm hệ số a của hàm số đã cho.
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến? Vì sao?