
![]() Ảnh minh họa
Ảnh minh họa
I. Yêu cầu[sửa]
Việc
dạy
học
các
khái
niệm
toán
học
ở
trường
THPT
phải
dần
dần
làm
cho
học
sinh
đạt
được
các
yêu
cầu
sau:
Bạn đang đọc: Dạy học khái niệm toán học
-
Nắm
vững[2]
các
đặc
điểm
đặc
trưng[3]
của
một
khái
niệm -
Biết
nhận
dạng
khái
niệm,
tức
là
biết
phát
hiện
xem
một
đối
tượng
cho
trước
có
thuộc
phạm
vi
một
khái
niệm
nào
đó
hay
không,
đồng
thời
biết
thể
hiện
khái
niệm,
nghĩa
là
biết
tạo
ra
một
đối
tượng
thuộc
phạm
vi
một
khái
niệm
cho
trước. -
Biết
phát
biểu
rõ
ràng,
chính
xác
định
nghĩa
của
một
số
khái
niệm[4] -
Biết
vận
dụng
khái
niệm
trong
những
tình
huống
cụ
thể
trong
hoạt
động
giải
toán
và
ứng
dụng
vào
thực
tiễn -
Nắm
được
mối
quan
hệ
của
khái
niệm
này
so
với
khái
niệm
khác
trong
một
hệ
thống
các
khái
niệm
Các nhu yếu trên đây có quan hệ ngặt nghèo với nhau, tuy nhiên vì lí do sư phạm, những nhu yếu trên không phải khi nào cũng được đặt ra với mức độ như nhau với mọi khái niệm. Chẳng hạn, khái niệm về ” hướng của vecto ” [ 5 ] không được nêu thành định nghĩa một cách tường minh mà chỉ được diễn đạt một cách trực quan dựa vào kinh nghiệm tay nghề sống của học viên. Nhưng với những khái niệm ” hàm số “, ” hàm số chẵn “, ” hàm số lẻ “, … thì lại nhu yếu học viên phải phát biểu được định nghĩa một cách đúng mực và vận dụng được khi giải toán .
II. Các con đường hình thành khái niệm[sửa]
1 ) Con đường quy nạp[sửa]
Theo
con
đường
này,
xuất
phát
từ
một
số
trường
hợp
cụ
thể
(như
mô
hình,
hình
vẽ,
thí
dụ
cụ
thể,…)
giáo
viên
dẫn
dắt
học
sinh
bằng
cách
trừu
tượng
hóa
và
khái
quát
hóa[6]
tìm
ra
dấu
hiệu
đặc
trưng
của
một
khái
niệm
thể
hiện
ở
những
trường
hợp
cụ
thể,
từ
đó
đi
đến
định
nghĩa
của
khái
niệm.
Cần phải tinh lọc một số lượng thích hợp những hình ảnh, thí dụ đơn cử, trong đó tín hiệu đặc cho khái niệm được đọng lại nguyên vẹn, còn những thuộc tính khác của những đối tượng người tiêu dùng thì đổi khác .
Quá trình tiếp cận một khái niệm theo con đường này thường diễn ra như sau :
-
Giáo
viên
đưa
ra
một
số
ví
dụ
cụ
thể
để
học
sinh
thấy
sự
tồn
tại
của
một
loạt
đối
tượng
nào
đó -
Giáo
viên
dẫn
dẫn
học
sinh
phân
tích,
so
sánh
và
nêu
bật
những
đặc
điểm
chung
của
các
đối
tượng
đang
được
xem
xét.[7] -
Giáo
viên
gợi
mở
để
học
sinh
phát
biểu
định
nghĩa
khái
niệm
bằng
cách
nêu
các
tính
chất
đặc
trưng
của
khái
niệm
Con đường này nên triển khai khi :
-
trình
độ
nhận
thức
học
sinh
còn
thấp[8]; -
vốn
kiến
thức
còn
chưa
nhiều
và
thường
được
sử
dụng
trong
điều
kiện:
chưa
phát
hiện
được
một
khái
niệm
nào
làm
điểm
xuất
phát
cho
con
đường
suy
diễn; -
đã
định
hình
được
một
số
đối
tượng
thuộc
ngoại
diên
của
khái
niệm
cần
hình
thành,
do
đó
đủ
vật
liệu
để
thực
hiện
phép
quy
nạp
Ví dụ, để hình thành khái niệm về phép biến hình theo con đường quy nạp, ta hoàn toàn có thể làm như sau :
-
Cho
điểm
O
cố
định,
với
điểm
M
tùy
ý
hãy
dựng
điểm
M’
là
điểm
đối
xứng
với
M
qua
O -
Cho
một
vecto

,
với
điểm
M
tùy
ý
hãy
dựng
điểm
M’
sao
cho
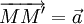
Qua 2 hoạt động giải trí trên, học viên nhận xét những đặc thù giống nhau ( với mỗi điểm M đều có một quy tắc để chỉ ra điểm M ‘ xác lập ) và khác nhau ( bộc lộ ở nội dung của quy tắc ấy ) ở hai hoạt động giải trí trên. Sau đó đi đến định nghĩa phép biến hình là một quy tắc sao cho ứng với mỗi điểm M ta hoàn toàn có thể chỉ ra một điểm M ‘ hoàn toán xác lập .
Xét một ví dụ khác, trước khi phát biểu định nghĩa đường thẳng song song với mặt phẳng, hoàn toàn có thể cho học viên xử lý bài toán sau : ” Chứng minh rằng nếu đường thẳng d song song với một đường thẳng a nằm trong mặt phẳng ( P. ) và nếu d không nằm trong ( P. ) thì đường thẳng d và mặt phẳng ( P. ) không có điểm chung “. Sau đó đi đến định nghĩa ” Đường thẳng d song song với mp ( P. ) nếu d tuy nhiên với một đường thẳng nằm trong ( P. ) và d không nằm trong mp ( P. ) ”
Quá trình hình thành khái niệm theo con đường quy nạp có công dụng tăng trưởng những năng lượng trí tuện như trừu tượng hóa, khái quá hóa, so sánh thuận tiện cho hoạt động giải trí tích cực của học viên. Tuy nhiên, con đường này yên cầu phải tốn nhiều thời hạn và cần có những điều kiện kèm theo đã nói trên .
2 ) Con đường suy diễn[sửa]
Con
đường
thứ
hai
là
con
đường
suy
diễn,
trong
đó
định
nghĩa
khái
niệm
mới
xuất
phát
từ
định
nghĩa
của
khái
niệm
mà
học
sinh
đã
biết
Quá trình tiếp cận một khái niệm theo con đường này thường diễn ra như sau :
-
Xuất
phát
từ
một
khái
niệm
đã
biết,
thêm
vào
nội
hàm
của
khái
niệm
đó
một
số
đặc
điểm
mà
ta
quan
tâm -
Phát
biểu
định
nghĩa
bằng
cách
nêu
tên
khái
niệm
mới
và
định
nghĩa
nó
nhờ
một
khái
niệm
tổng
quát
hơn
cùng
với
những
đặc
điểm
hạn
chế
một
bộ
phận
trong
khái
niệm
tổng
quát
đó -
Đưa
ra
ví
dụ
đơn
giản
minh
họa
cho
khái
niệm
vừa
được
định
nghĩa
Con đường này nên thực thi khi :
-
trình
độ
nhận
thức
của
học
sinh
đã
khá
hơn[9] -
vốn
kiến
thức
đã
nhiều
lên -
phát
hiện
ra
một
khái
niệm
làm
điểm
xuất
phát
cho
con
đường
suy
diễn
Ví dụ, hoàn toàn có thể hình thành khái niệm phép vị tự cho học viên theo con đường suy diễn bằng cách dựa vào phép biến hình đã được học trước đó như sau :
-
“Cho
một
điểm
O
và
số
k
≠
0,
phép
biến
hình
biến
một
điểm
M
bất
kì
thành
điểm
M’
sao
cho
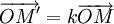
gọi
là
phép
vị
tự
tâm
O
tỉ
số
k”.
Sau khi định nghĩa theo con đường này, thiết yếu phải lấy ví dụ đơn cử để chứng tỏ rằng khái niệm được định nghĩa như vậy thực sự sống sót .
Ví dụ, sau khi phát biểu định nghĩa đường vuông góc chung của hai đường thẳng chéo nhau a, b [ 10 ] nên cho học viên xác lập đường vuông góc chung của những cặp cạnh đối lập của một tứ diện đều, hoặc đường vuông góc chung của những cặp đường thẳng AB và A’D ‘, AA ‘ và BD ‘, … của hình lập phương ABCD.A ‘ B’C ‘ D ‘ .
Con đường hình thành khái niệm này có tính năng tốt để phát huy tính dữ thế chủ động và phát minh sáng tạo cho học viên [ 11 ], tiết kiệm chi phí thời hạn. Tuy nhiên con đường này hạn chế tăng trưởng năng lượng trí tuệ chung như nghiên cứu và phân tích, tổng hợp, so sánh …
III. Các hoạt động giải trí dạy học khái niệm[sửa]
1 ) Định nghĩa khái niệm[sửa]
a ) Các cách định nghĩa[sửa]
Việc hình thành khái niệm thường kết thúc bằng định nghĩa khái niệm. Trong toán học và trong giảng dạy toán học có những cách khác nhau để định nghĩa khái niệm .
Định
nghĩa
bằng
cách
nêu
rõ
loại
và
chủng
là
cách
định
nghĩa
có
cấu
trúc
dạng
B(x)
⇔
A(x)
và
P(x)
Xét tập hợp T gồm những thành phần x có đặc thù A và trong T có những thành phần mang đặc thù P. nào đó và những thành phần không có đặc thù này, thì nhờ đặc thù P., ta chia tập hợp T thành hai tập hợp con không rỗng, không giao nhau :
-
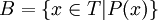
và
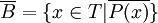
Như vậy một thành phần có đặc thù B thì phải có đặc thù A và P. và viết là : B ( x ) ⇔ A ( x ) và P. ( x )
Trong
cấu
trúc
trên,
tính
chất
B
gọi
là
tính
chất
của
khái
niệm
chủng
còn
tính
chất
A
là
tính
chất
của
một
khái
niệm
loại,
thường
là
loại
gần
nhất
với
đối
tượng/phần
tử
x
được
định
nghĩa,
còn
P
là
sự
khác
biệt
đặc
trưng[12]
giữa
các
đối
tượng
có
tính
chất
B
và
các
đối
tượng
còn
lại
mang
tính
chất
A.
Ví dụ, trong định nghĩa phép vị tự nói trên, một phép biến hình là phép vị tự ( B ) khi và chỉ khi phép biến hình ấy ( A ) và có đặc thù ( P. ) biến mỗi điểm M thành điểm M ‘ sao cho
Định
nghĩa
như
vậy
là
tường
minh,
trong
đó
các
khái
niệm
được
định
nghĩa
và
khái
niệm
dùng
để
định
nghĩa
là
tách
bạch
với
nhau.
Điều
đó
cho
phép
ta
thay
thế
cái
được
định
nghĩa
bằng
cái
dùng
để
định
nghĩa
hay
ngược
lại.
Sự
thay
thế
như
vậy
rất
hay
được
sử
dụng
khi
chứng
minh
định
lý
hay
giải
toán.
Chú ý rằng, định nghĩa bằng cách nêu rõ loại và chủng như trên phải thỏa mãn nhu cầu nhu yếu logic sau : ” Trong tập hợp T có những thành phần có đặc thù P. và có những thành phần không có đặc thù P. ” .
Tất
nhiên,
không
phải
tất
cả
các
khái
niệm
toán
học
đều
được
định
nghĩa
theo
cấu
trúc
trên,
vì
sẽ
có
những
khái
niệm
xuất
phát
đầu
tiên
không
được
định
nghĩa
thông
qua
khái
niệm
nào
khác[13].
Những
khái
niệm
này
được
định
nghĩa
một
cách
không
tường
minh,
giáp
tiếp
bằng
mô
tả
để
làm
nổi
bật
nội
dung
của
chúng
(ở
trình
độ
thấp)
hay
bằng
những
tiên
đề
(ở
trình
độ
xây
dựng
lí
thuyết
chặt
chẽ),
chẳng
hạn
như
khái
niệm
“điểm”[14],
“đường
thẳng”,
“hướng
của
vecto”,…
Như vậy, khi nói rằng những khái niệm ” điểm “, ” đường thẳng “, ” mặt phẳng ” là những khái niệm xuất phát nên không được định nghĩa thì phải hiểu là ” chúng không được định nghĩa tường minh qua những khái niệm khác ” .
Tóm lại, trong dạy học ở trường đại trà phổ thông, có những khái niệm không được định nghĩa vì hai lí do khác nhau : hoặc vì chúng là những khái niệm xuất phát trong khoa học toán học, hoặc vì lí do sư phạm. [ 15 ] Đối với những khái niệm như vậy thì cần miêu tả, lý giải trải qua những ví dụ đơn cử để giúp học viên tưởng tượng được hình ảnh, hiểu được ý nghĩa của khái niệm ấy .
Trong những khái niệm toán học, có những khái niệm về một đối tượng người tiêu dùng và có những khái niệm về một quan hệ. Chẳng hạn, định nghĩa như sau : ” Vecto là một đoạn thẳng trong đó đã chỉ rõ điểm mút nào là điểm đầu và điểm mút nào là điểm cuối ” là một khái niệm về một đối tượng người dùng. Nhưng, định nghĩa ” Đường thẳng d gọi là vuông góc với mp ( P. ) nếu nó vuông góc với mọi đường thẳng của mp ( P. ). ” lại là một khái niệm về một quan hệ .
Trong cách định nghĩa về một khái niệm quan hệ, rõ ràng đó là một cách định nghĩa tường minh nhưng không hề tách được khái niệm loại gần nhất và sự độc lạ đặc trưng .
b ) Các nhu yếu của một định nghĩa[sửa]
Đối với một định nghĩa, ta không hề nói rằng nó đúng hay sai. Một định nghĩa hoàn toàn có thể hài hòa và hợp lý ( gật đầu được ) hay không hài hòa và hợp lý ( không đồng ý được ) nhờ vào vào sự thỏa mãn nhu cầu hay không thỏa mãn nhu cầu những nhu yếu tối thiểu của định nghĩa .
Yêu cầu quan trọng nhất là định nghĩa không được vòng quanh. Việc vi phạm nguyên tắc này biểu lộ ở chỗ cái được định nghĩa lại tiềm ẩn ( tường minh hay không tường minh ) trong cái dùng để định nghĩa. Chẳng hạn :
-
“Góc
được
gọi
là
góc
vuông
nếu
hai
cạnh
của
nó
vuông
góc
với
nhau” -
“Hai
đường
thẳng
gọi
là
vuông
góc
với
nhau
nếu
chúng
tạo
thành
một
góc
vuông”
Sự vòng quanh bộc lộ ở chỗ : trong định nghĩa thứ nhất, góc vuông được định nghĩa qua những đường thẳng vuông góc, còn trong định nghĩa thứ hai thì khái niệm thứ hai lại được định nghĩa qua khái niệm thứ nhất .
Yêu cầu thứ hai nhằm mục đích bảo vệ sự đúng đắn ( chuẩn mực ) của một định nghĩa, đó là định nghĩa phải có trị nhưng không được đa trị. Định nghĩa phải có trị tức là phải sống sót tối thiểu một đối tượng người dùng thỏa mãn nhu cầu những điều kiện kèm theo trong định nghĩa. Định nghĩa không được đa trị tức là mỗi thuật ngữ hay kí hiệu chỉ được dùng để chỉ một cái được định nghĩa. Ví dụ về sự vi phạm này là việc dùng cùng một kí hiệu ” AB ” để chỉ những đối tượng người dùng ” đường thẳng đi qua đoạn thẳng với hai đầu mút là A và B “, ” độ dài đoạn thẳng AB “, ” tia với điểm gốc A và chứa điểm B “, ” vecto với điểm đầu A và điểm cuối B “, … Vì vậy trong sách giáo kha, người ta phải đặt trước kí hiệu này thuật ngữ chỉ loại đối tượng người tiêu dùng như ” đoạn thẳng AB “, ” tia AB “, … hoặc kèm theo kí hiệu bổ trợ .
2 ) Củng cố khái niệm[sửa]
Để củng cố khái niệm cho học viên, giáo viên cần cho học viên tập luyện những hoạt động giải trí : nhận dạng và biểu lộ khái niệm, hoạt động giải trí ngôn từ, khái quát hóa và đặc biệt quan trọng hóa, hệ thống hóa khái niệm, vận dụng khái niệm, …
a)
Nhận
dạng
và
thể
hiện
Một
trong
những
biểu
hiện
của
chủ
nghĩa
hình
thức
trong
quá
trình
học
môn
toán
là
học
sinh
học
thuộc
cách
phát
biểu
định
nghĩa
nhưng
lại
không
nhận
biết
được
một
đối
tượng
cụ
thể
trong
những
tình
huống
khác
nhau
có
thỏa
mãn
định
nghĩa
ấy
hay
không,
không
tự
mình
tạo
ra
được
những
đối
tượng
thỏa
mãn
định
nghĩa.
Vì
vậy,
cần
phải
cho
học
sinh
tiến
hành
những
hoạt
động
“nhận
dạng”
và
“thể
hiện”
để
tránh
và
khắc
phục
tình
trạng
này.
Ví dụ : Sau khi học viên đã biết định nghĩa hai đường thẳng song song, hai đường thẳng chéo nhau thì nên cho họ thực thi những hoạt động giải trí nhận dạng và biểu lộ như
-
Quan
sát
một
tứ
diện
và
có
nhận
xét
gì
về
vị
trí
tương
đối
của
sáu
đường
thẳng
chứa
sáu
cạnh?[16] -
Muốn
tạo
thêm
những
cặp
đường
thẳng
chéo
nhau,
ta
chỉ
cần
lấy
trung
điểm
của
hai
cạnh
đối
diện
nào
đó
rồi
xét
vị
trí
tương
đối
của
đường
thẳng
đi
qua
hai
trung
điểm
đó
và
các
đường
khác -
Cho
trước
hai
đường
thẳng
chéo
nhau
a,
b
và
xét
hai
đường
thẳng
phân
biệt
c,
d
cắt
cả
a
lẫn
b
thì
c
và
d
không
thể
là
hai
đường
thẳng
song
song[17]
Việc nhận dạng và bộc lộ khái niệm hoàn toàn có thể dựa vào định nghĩa khái niệm cũng hoàn toàn có thể dựa vào những điều kiện kèm theo cần, điều kiện kèm theo đủ khác .
Ví dụ, để nhận dạng và bộc lộ khái niệm ” Hai đường thẳng song song trong khoảng trống ” thì ngoài định nghĩa ” Trong khoảng trống, hai đường thẳng song song với nhau nếu chúng không có điểm chung và cùng nằm trên một mặt phẳng nào đó ” thì còn hoàn toàn có thể sử dụng định lí ” Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau ” hoặc định lí ” Một mp ( P. ) cắt hai mặt phẳng phân biệt ( Q. ) và ( R ) theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc đôi một song song ” .
b)
Hoạt
động
ngôn
ngữ
Để giúp học viên củng cố khái niệm và tăng trưởng ngôn từ, cần chú ý quan tâm hướng dẫn và khuyến khích họ diễn đạt một định nghĩa dưới nhiều hình thức khác nhau, bằng lời lẽ của bản thân .
c)
Khái
quát
hóa,
đặc
biệt
hóa
Khái quát hóa khái niệm – một hoạt động giải trí quan trọng cần rèn luyện cho học viên. Chẳng hạn, từ khái niệm tiếp tuyến của một đường tròn tới khái niệm tiếp tuyến của một đường cong, từ những khái niệm tốc độ tức thời của một chuyển đọng, thông số góc của một tiếp tuyến tới khái niệm đạo hàm của một hàm số, … trái lại với hoạt động giải trí khái quát hóa là đặc biệt quan trọng hóa
d)
Hệ
thống
hóa
Hệ thống hóa khái niệm, tức là biết nhận ra những mối quan hệ giữa những khái niệm, ví dụ như khái niệm tiếp tuyến của một đường tròn là một trường hợp riêng của khái niệm tiếp tuyến của một đường cong, khái niệm đạo hàm là một khái niệm khái quát của khái niệm tốc độ tức thời, …
e)
Vận
dụng
Sau khi truyền thụ một khái niệm, cần tạo thời cơ cho học viên vận dụng nó vào những bài toán, những hoạt động giải trí khác nhau, đặc biệt quan trọng là những bài toán chứng tỏ. Điều đó vừa có tính năng củng cố, đào sâu khái niệm, lại vừa góp thêm phần tăng trưởng năng lượng giải toán .
Trong những hoạt động giải trí trên thì hoạt động giải trí ” nhận dạng và bộc lộ ” khái niệm có vai trò đặc biệt quan trọng quan trọng vì những hoạt động giải trí này có công dụng tích cực không riêng gì trong quá trình củng cố khái niệm mà còn cả trong quá trình hình thành khái niệm và vận dụng khái niệm, không chỉ có vậy chúng là giải pháp đa phần để chống và khắc phục chủ nghĩa hình thức trong học tập. [ 18 ]
3 ) Phân chia khái niệm[sửa]
Biết phân loại khái niệm là một trong những biểu lộ của việc nắm vững khái niệm toán học [ 19 ] cũng như những khái niệm thuộc môn học khác. Chẳng hạn, học viên sẽ nắm vững khái niệm hàm số hơn nếu cùng với việc hiểu định nghĩa, học viên còn biết rằng có những hàm số chẵn và hàm số không chẵn, những hàm số lẻ và hàm số không lẻ .
Nhiều khi, học viên phải nắm vững chẳng những định nghĩa mà cả cách phân loại khái niệm mới hoàn toàn có thể giải toán hay xem xét những yếu tố tương quan. Chẳng hạn :
-
khi
giải
và
biện
luận
phương
trình
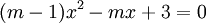
học
sinh
phải
xét
trường
hợp
m
=
1
phương
trình
trở
thành
phương
trình
bậc
nhất
thì
giải
theo
kiểu
phương
trình
bậc
nhất
và
trường
hợp
m
≠
1
phương
trình
đã
cho
là
phương
trình
bậc
hai
thì
giải
theo
kiểu
phương
trình
bậc
hai -
xét
bài
toán
“Chứng
minh
lăng
trụ
có
sáu
mặt
đều
là
hình
thoi
bằng
nhau
là
một
lăng
trụ
xiên” -
hay
một
ví
dụ
khác
là
khi
giải
và
biện
luận
bất
phương
trình
bậc
nhất
ax
+
b
>
0
ta
phải
xét
tất
cả
các
trường
hợp
của
hệ
số
a:
a
>
0,
a
=
0
và
a
< 0. -
xét
bài
toán
“Cho
hai
đường
thẳng
phân
biệt
a
và
b
cùng
vuông
góc
với
một
mặt
phẳng
(P).
Xét
vị
trí
tương
đối
giữa
hai
đường
thẳng
a
và
b”[20]
Thực tiễn dạy học cho thấy, giáo viên cần khai thác và sử dụng tốt những bài tập dạng trắc nghiệm khách quan kiểu ” Các mệnh đề sau đây đúng hay sai : A ) … B ) … ” vì có công dụng tốt trong việc rèn luyện cho học viên kĩ năng phân loại khái niệm. [ 21 ] Muốn vấn đáp đúng câu hỏi, học viên cần triển khai phân loại khái niệm, tức là xét tổng thể những năng lực hoàn toàn có thể xảy ra. Chẳng hạn, xét bài toán sau ” Mệnh đề ‘ nếu a ⊥ b và a ⊥ c thì b / / c ‘ đúng hay sai ? “. Để giải bài toán này, học viên hoàn toàn có thể tâm lý : hai đường thẳng bất kỳ hoàn toàn có thể song song, chéo nhau, cắt nhau. Nếu mệnh đề trên đúng thì không hề xảy ra trường hợp b và c chéo nhau và cũng không hề xảy ra trường hợp b và c cắt nhau. Xét hai đường thẳng cắt nhau b và c nào đó, liệu có một đường thẳng a nào vuông góc với cả hai đường b và c không ? Từ đó tìm ra giải thuật bài toán .
Biết phân loại khái niệm mới hoàn toàn có thể hệ thống hóa những khái niệm sau mỗi phần, mỗi chương, … [ 22 ] Chẳng hạn, hoàn toàn có thể mạng lưới hệ thống khái niệm hình lăng trụ và hình hộp bằng sơ đồ Ven
Việc phân loại, mạng lưới hệ thống những khái niệm [ 23 ] vượt xa ra khỏi khoanh vùng phạm vi của việc nắm vững những kỹ năng và kiến thức toán học, nó thiết yếu cho bất kỳ nghành hoạt động giải trí nào của con người. Vì thế, những tri thức và kĩ năng về mặt này cần được quan tâm thích đáng .
IV. Trình tự truyền thụ một khái niệm mới[sửa]
Trình tự truyền thụ một khái niệm mới thường gồm có [ 24 ] những hoạt động giải trí sau :
-
Dẫn
học
sinh
vào
khái
niệm:
giúp
học
sinh
tiếp
cận
khái
niệm,
có
thể
thực
hiện
được
bằng
cách
thông
qua
một
ví
dụ
hoặc
một
hiện
tượng
có
trong
thực
tiễn,… -
Hình
thành
khái
niệm:
giúp
học
sinh
có
được
khái
niệm,
có
thể
thực
hiện
được
bằng
cách
khái
quát
hoát,… -
Củng
cố
khái
niệm:
thông
qua
các
hoạt
động
nhận
dạng,
thể
hiện,
ngôn
ngữ.
Khắc
sâu
kiến
thức
thông
qua
ví
dụ
và
phản
ví
dụ -
Bước
đầu
vận
dụng
khái
niệm
trong
bài
tập
đơn
giản -
Vận
dụng
khái
niệm
trong
bài
tập
tổng
hợp
Tài liệu tìm hiểu thêm[sửa]
-
Phương
pháp
dạy
học
môn
Toán,
Nguyễn
Bá
Kim,
Vũ
Dương
Thụy,
NXB
Giáo
dục,
2000,
trang
179
–
192 -
Tài
liệu
bồi
dưỡng
giáo
viên
thực
hiện
chương
trình,
sách
giáo
khoa
lớp
10
môn
Toán,
NXB
Giáo
dục,
2007,
trang
98
–
100 -
Phương
pháp
dạy
học
môn
Toán
phần
hai,
Nguyễn
Bá
Kim,
Đinh
Nho
Chương,
Nguyễn
Mạnh
Cường,
Vũ
Dương
Thụy,
Nguyễn
Văn
Thường,
NXB
Giáo
dục,
trang
179
–
185;
310
–
311;
319
–
325 -
Tập
tin:Phuong-phap-day-hoc-cac-tinh-huong-dien-hinh-trong-mon-Toan-Le-Van-Tien-2005.pdf,
Lê
Văn
Tiến,
Trường
Đại
học
Sư
phạm
TP.
Hồ
Chính
Minh -
Tập
tin:Vai
net
ve
day
hoc
khai
niem
ham
so
o
truong
pho
thong.pdf
–
Luận
văn
của
sinh
viên
Đào
Thị
Mừng,
Đại
học
An
Giang,
2008
Chú thích[sửa]
-
↑Thực tiễn dạy học cho thấy, học viên không giải được bài toán phần nhiều là do không hiểu khái niệm toán học tiềm ẩn trong câu hỏi của đề toán . -
↑Theo từ điển tiếng Việt : Nắm vững nghĩa là hiểu biết thấu đáo -
↑Hay
còn
gọi
là
dấu
hiệu
đặc
trưng.
Theo
từ
điển
tiếng
Việt:
Đặc
trưng
là
điểm
nổi
bật,
giúp
phân
biệt
cá
thể
đã
cho
với
các
cá
thể
khác
mà
ta
có
thể
đem
ra
so
sánh -
↑Phát biểu chính xác định nghĩa không có nghĩa là phải phát biểu giống như định nghĩa có trong SGK ! -
↑Hay còn gọi là ” chiều của vecto “ -
↑Trừu tượng hóa, khái quát hóa là những thao tác tư duy -
↑Có thể có cả những đối tượng người dùng không có những đặc thù đó -
↑Mới biết suy luận dưới Lever 3 – theo những Lever tư duy của Van Hiele -
↑Đã biết suy luận từ Lever 3 – suy diễn không hình thức – trở lên -
↑Đoạn thẳng cắt cả a và b đồng thời vuông góc với cả a và b -
↑Thông qua hoạt động giải trí bộc lộ khái niệm . -
↑Còn gọi là tín hiệu đặc trưng hay đặc thù đặc trưng -
↑Trước chúng không có một khái niệm nào. Từ ” Root ” đúng cho trường hợp này. – 😀 -
↑Một dấu chấm nhỏ trên trang giấy là hình ảnh của một điểm -
↑Mặc dù chúng hoàn toàn có thể được định nghĩa trong khoa học toán học . -
↑có ba cặp đường thẳng chéo nhau ( ba cặp đối lập ), bốn bộ ba đường thẳng đồng quy, không có cặp nào song song -
↑Có thể đặt thêm câu hỏi : c và d hoàn toàn có thể cắt nhau không ? -
↑Học sinh có nắm vững những tín hiệu đặc trưng của khái niệm thì mới hoàn toàn có thể nhận dạng và bộc lộ được khái niệm . -
↑Có biết nhận dạng và biểu lộ khái niệm thì mới biết phân loại khái niệm -
↑Phân chia những trường hợp : a / / b ; a cắt b và a, b chéo nhau -
↑Hơn nữa kiểu bài tập này thường ngắn nên rất tương thích với thời hạn của một tiết học . -
↑Có
thể
dùng
sơ
đồ
Ven,
sơ
đồ
khối,
bảng,… -
↑Một trong những hoạt động giải trí quan trọng của hoạt động giải trí trí tuệ -
↑Không nhất thiết phải luôn đủ và đúng theo thứ tự
Bài liên quan
Source: https://futurelink.edu.vn
Category: Tài liệu Toán học