Chứng minh Bất đẳng thức Bunhiacopxki kèm ví dụ minh họa

Bởi
Bất đẳng thức Bunhiacopxki, những dạng BĐT Bunhiacopxki trong chương trình học, chứng tỏ và nhận dạng sai lầm đáng tiếc hay gặp khi vận dụng Bunhiacopxki vào những bài toánCùng Đọc tài liệu điểm danh những kiến thức và kỹ năng cơ bản so với BĐT Bunhiacopxki em nhé :

Kiến thức cơ bản

Bất đẳng thức Bunhiacopxki dạng thường thì

1. Dạng bài toán áp dụng bất đẳng thức này khá thông dụng trong chương trình học của các em:

( a² + b² ) ( c² + d² ) ≥ ( ac + bd ) ²

Chứng minh: 

( a² + b² ) ( c² + d² ) ≥ ( ac + bd ) ²↔ ( ac ) ² + ( ad ) ² + ( bc ) ² + ( bd ) ² ≥ ( ac ) ² + 2 abcd + ( bd ) ²↔ ( ad ) ² + ( bc ) ² ≥ 2 abcd ↔ ( ad ) ² – 2 abcd + ( bc ) ² ≥ 0 ↔ ( ad – bc ) ² ≥ 0 => luôn đúngDấu ” = ” xảy ra khi \ ( { \ displaystyle { \ frac { a } { c } } = { \ frac { b } { d } } } \ )

2. Với a,b,x,y là các số thực, ta có các bất đẳng thức sau:

– \ ( ( ax + by ) ^ 2 \ le ( a ^ 2 + b ^ 2 ) ( x ^ 2 + y ^ 2 ) \ )Dấu bằng xảy ra khi \ ( { \ displaystyle { \ frac { x } { a } } = { \ frac { y } { b } } } \ )- \ ( \ dfrac { ( a + b ) ^ 2 } { x + y } \ le \ dfrac { a ^ 2 } { x } + \ dfrac { b ^ 2 } { y } \ )( với x, y > 0, a, b là số thực )

3. Với bộ 3 số a, b, c và x, y, z ta có:

– \ ( ( ax + by + cz ) ^ 2 \ le ( a ^ 2 + b ^ 2 + c ^ 2 ) ( x ^ 2 + y ^ 2 + z ^ 2 ) \ )Dấu bằng xảy ra khi \ ( \ dfrac { x } { a } = \ dfrac { y } { b } = \ dfrac { z } { c } \ )- \ ( \ dfrac { ( a + b + c ) ^ 2 } { x + y + z } \ le \ dfrac { a ^ 2 } { x } + \ dfrac { b ^ 2 } { y } + \ dfrac { c ^ 2 } { z } \ )( x, y, z > 0, a, b là số thực )

Bất đẳng thức Bunhiacopxki tổng hợp

Dạng 1Cho hai dãy số thực \ ( ​ ​ ​ ​ a_ { 1 }, a_ { 2 }, … a_ { n } \ ) và \ ( b_ { 1 }, b_ { 2 }, … b_ { n } \ ) ta có :\ ( ( a_ { 1 } b_ { 1 } + a_ { 2 } b_ { 2 } + … + a_ { n } b_ { n } ) ^ { 2 } \ leq ( a_ { 1 } ^ { 2 } + a_ { 2 } ^ { 2 } … + a_ { n } ^ { 2 } ) ( b_ { 1 } ^ { 2 } + b_ { 2 } ^ { 2 } … + b_ { n } ^ { 2 } ) \ )Dấu ” = ” xảy ra khi và chỉ khi \ ( \ displaystyle \ frac { { { a } _ { 1 } } } { { { b } _ { 1 } } } = \ frac { { { a } _ { 2 } } } { { { b } _ { 2 } } } = … = \ frac { { { a } _ { n } } } { { { b } _ { n } } } \ ) với quy ước nếu mẫu bằng 0 thì tử phải bằng 0Đây là công thức do ba nhà toán học độc lập Cauchy – Bunhiacopxki – Schwarz phát hiện và yêu cầu .

Chứng minh: 

Đặt \ ( A = a_ { 1 } ^ { 2 } + a_ { 2 } ^ { 2 } + … + a_ { n } ^ { 2 }, B = b_ { 1 } ^ { 2 } + b_ { 2 } ^ { 2 } + … + b_ { n } ^ { 2 }, C = a_ { 1 } b_ { 1 } + a_ { 2 } b_ { 2 } + … + a_ { n } b_ { n } \ )=> Chúng ta cần phải chứng tỏ được A.B > C²Nếu A = 0 thì \ ( ​ ​ ​ ​ a_ { 1 } = a_ { 2 } = … a_ { n } \ ), bất đẳng thức được chứng tỏ. Cũng vậy nếu B = 0. Do đó ta chỉ cần xét trường hợp A và B khác 0Với mọi x ta có :\ ( ( a_ { 1 } x-b_ { 1 } ) ^ { 2 } \ geq 0 \ Rightarrow a_ { 1 } ^ { 2 } x ^ { 2 } – 2 a_ { 1 } b_ { 1 } x + b_ { 1 } ^ { 2 } \ geq 0 \ )\ ( ( a_ { 2 } x-b_ { 2 } ) ^ { 2 } \ geq 0 \ Rightarrow a_ { 2 } ^ { 2 } x ^ { 2 } – 2 a_ { 2 } b_ { 2 } x + b_ { 2 } ^ { 2 } \ geq 0 \ )………\ ( ( a_ { n } x-b_ { n } ) ^ { 2 } \ geq 0 \ Rightarrow a_ { n } ^ { 2 } x ^ { 2 } – 2 a_ { n } b_ { n } x + b_ { n } ^ { 2 } \ geq 0 \ )Cộng từng vế của những bất đẳng thức trên được :\ ( ( a_ { 1 } ^ { 2 } + a_ { 2 } ^ { 2 } + … + a_ { n } ^ { 2 } ) x ^ { 2 } – 2 ( a_ { 1 } b_ { 1 } + a_ { 2 } b_ { 2 } + … + a_ { n } b_ { n } ) x + ( b_ { 1 } ^ { 2 } + b_ { 2 } ^ { 2 } + … + b_ { n } ^ { 2 } ) \ geq 0 \ )

tức là Ax² – 2Cx + B ≥ 0 (1)

Vì ( 1 ) đúng với mọi x nên thay \ ( x = \ frac { C } { A } \ ) vào ( 1 ) ta được :\ ( A. \ frac { C ^ { 2 } } { A ^ { 2 } } – 2. \ frac { C ^ { 2 } } { A } + B \ geq 0 \ Rightarrow B – \ frac { C ^ { 2 } } { A } \ geq 0 \ Rightarrow AB-C ^ { 2 } \ geq 0 \ Rightarrow AB \ geq C ^ { 2 } \ )Xảy ra đẳng thức khi và chỉ khi\ ( a_ { 1 } x = b_ { 1 }, a_ { 2 } x = b_ { 2 }, …, a_ { n } x = b_ { n } \ )tức là \ ( \ displaystyle \ frac { { { a } _ { 1 } } } { { { b } _ { 1 } } } = \ frac { { { a } _ { 2 } } } { { { b } _ { 2 } } } = … = \ frac { { { a } _ { n } } } { { { b } _ { n } } } \ ) với quy ước rằng nếu mẫu bằng 0 thì tử phải bằng 0 => đpcm

Một số dạng Bất đẳng thức Bunhiacopxki khác mà em có thể tham khảo:

Dạng 2 :\ ( \ displaystyle \ sqrt { \ left ( a_ { 1 } ^ { 2 } + a_ { 2 } ^ { 2 } + … + a_ { n } ^ { 2 } \ right ) \ left ( b_ { 1 } ^ { 2 } + b_ { 2 } ^ { 2 } + … + b_ { n } ^ { 2 } \ right ) } \ ge \ left | { { a } _ { 1 } } { { b } _ { 1 } } + { { a } _ { 2 } } { { b } _ { 2 } } + … + { { a } _ { n } } { { b } _ { n } } \ right | \ )Dấu ” = ” xảy ra khi và chỉ khi \ ( \ displaystyle \ frac { { { a } _ { 1 } } } { { { b } _ { 1 } } } = \ frac { { { a } _ { 2 } } } { { { b } _ { 2 } } } = … = \ frac { { { a } _ { n } } } { { { b } _ { n } } } \ )Dạng 3 :\ ( \ displaystyle \ sqrt { \ left ( a_ { 1 } ^ { 2 } + a_ { 2 } ^ { 2 } + … + a_ { n } ^ { 2 } \ right ) \ left ( b_ { 1 } ^ { 2 } + b_ { 2 } ^ { 2 } + … + b_ { n } ^ { 2 } \ right ) } \ ge { { a } _ { 1 } } { { b } _ { 1 } } + { { a } _ { 2 } } { { b } _ { 2 } } + … + { { a } _ { n } } { { b } _ { n } } \ )Dấu ” = ” xảy ra khi và chỉ khi \ ( \ displaystyle \ frac { { { a } _ { 1 } } } { { { b } _ { 1 } } } = \ frac { { { a } _ { 2 } } } { { { b } _ { 2 } } } = … = \ frac { { { a } _ { n } } } { { { b } _ { n } } } ≥ 0 \ )Dạng 4 :Cho hai dãy số tùy ý \ ( ​ ​ ​ ​ a_ { 1 }, a_ { 2 }, …, a_ { n } \ ) và \ ( x_ { 1 }, x_ { 2 }, …, x_ { n } \ ) ta có : với \ ( x_ { 1 }, x_ { 2 }, …, x_ { n } \ ) > 0Khi đó ta có :\ ( \ displaystyle \ frac { a_ { 1 } ^ { 2 } } { { { x } _ { 1 } } } + \ frac { a_ { 2 } ^ { 2 } } { { { x } _ { 2 } } } + … + \ frac { a_ { n } ^ { 2 } } { { { x } _ { n } } } \ ge \ frac { { { \ left ( { { a } _ { 1 } } + { { a } _ { 2 } } + … + { { a } _ { n } } \ right ) } ^ { 2 } } } { { { x } _ { 1 } } + { { x } _ { 2 } } + … + { { x } _ { n } } } \ )Dấu bằng xảy ra khi : \ ( \ displaystyle \ frac { { { a } _ { 1 } } } { { { x } _ { 1 } } } = \ frac { { { a } _ { 2 } } } { { { x } _ { 2 } } } = … = \ frac { { { a } _ { n } } } { { { x } _ { n } } } \ ge 0 \ )

Lưu ý khi đổi khác bất đẳng thức Bunhiacopxki

Với bất đẳng thức ba biến a, b, c ta hoàn toàn có thể sử dụng một số ít phép biến hóa như :

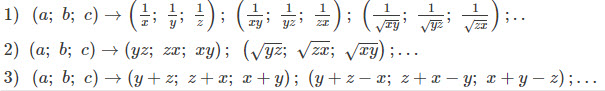
biến đổi bất đẳng thức Bunhiacopxki 1

Với 1 số ít bất đẳng thức có giả thiết là ta hoàn toàn có thể đổi biến :

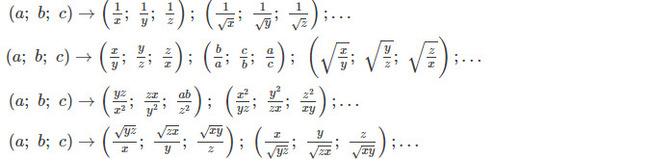
biến đổi bất đẳng thức Bunhiacopxki 2

Sai lầm thường gặp khi vận dụng Bunhiacopxki

Cho a là số thức dương thỏa mãn nhu cầu a ≥ 2. Tìm giá trị nhỏ nhất của biểu thức :\ ( \ displaystyle A = { { a } ^ { 2 } } + \ frac { 1 } { { { a } ^ { 2 } } } \ )Hướng dẫn :

sai lầm hay gặp phải khi áp dụng bất đẳng thức Bunhiacopxki

Ví dụ minh họa

Tham khảo 2 bài toán vận dụng Bất đẳng thức Bunhiacopxki trong những bài toán thường gặp :Bài toán 1 : Cho a, b, là những số thực dương thỏa mãn nhu cầu. Tìm giá trị nhỏ nhất của biểu thức :\ ( \ displaystyle A = \ sqrt { { { a } ^ { 2 } } + \ frac { 1 } { { { a } ^ { 2 } } } } + \ sqrt { { { b } ^ { 2 } } + \ frac { 1 } { { { b } ^ { 2 } } } } \ )

Bài làm:

Áp dụng bất đẳng thức Bunhiacopxki ta có :\ ( \ displaystyle \ left \ { \ begin { array } { l } \ sqrt { { { a } ^ { 2 } } + \ frac { 1 } { { { a } ^ { 2 } } } } = \ frac { 1 } { \ sqrt { 17 } }. \ sqrt { \ left ( { { a } ^ { 2 } } + \ frac { 1 } { { { a } ^ { 2 } } } \ right ). \ left ( { { 4 } ^ { 2 } } + { { 1 } ^ { 2 } } \ right ) } \ ge \ frac { 1 } { \ sqrt { 17 } } \ left ( 4 a + \ frac { 1 } { a } \ right ) \ \ \ sqrt { { { b } ^ { 2 } } + \ frac { 1 } { { { b } ^ { 2 } } } } = \ frac { 1 } { \ sqrt { 17 } }. \ sqrt { \ left ( { { b } ^ { 2 } } + \ frac { 1 } { { { b } ^ { 2 } } } \ right ). \ left ( { { 4 } ^ { 2 } } + { { 1 } ^ { 2 } } \ right ) } \ ge \ frac { 1 } { \ sqrt { 17 } } \ left ( 4 b + \ frac { 1 } { b } \ right ) \ end { array } \ right. \ )

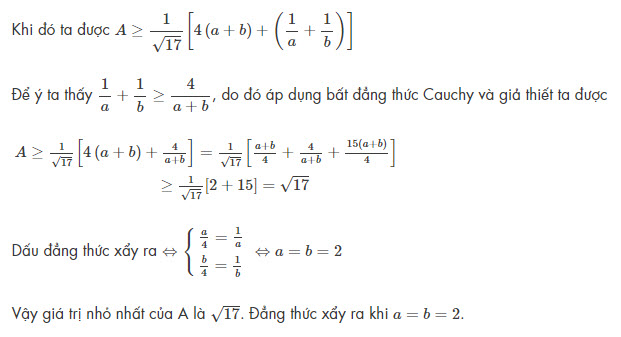
bài toán áp dụng bất đẳng thức Bunhiacopxki số 1

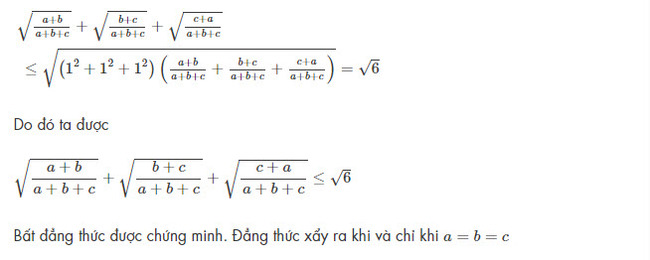
Bài toán 2 : Cho a, b, c là những số thực dương bất kể. Chứng minh rằng :

\(\displaystyle \sqrt{\frac{a+b}{a+b+c}}+\sqrt{\frac{b+c}{a+b+c}}+\sqrt{\frac{c+a}{a+b+c}}\le \sqrt{6}\)

Bài làm

Áp dụng BĐT Bunhiacopxki ta được

bài toán áp dụng bất đẳng thức Bunhiacopxki số 2