Bạn đang đọc: Công thức bất phương trình
5/5 – ( 1 bầu chọn )
Bất phương trình quy về bậc nhất

Giải và biện luận bpt dạng ax + b < 0

Hệ bất phương trình bậc nhất một ẩn
Muốn giải hệ bất phương trình bậc nhất một ẩn ta giải từng bất phương trình của hệ rồi lấy giao những tập nghiệm thu sát hoạch được .
Dấu nhị thức bậc nhất

Bất phương trình tích
∙ Dạng : P ( x ). Q ( x ) > 0 ( 1 ) ( trong đó P ( x ), Q. ( x ) là những nhị thức bậc nhất. )
∙ Cách giải : Lập bxd của P ( x ). Q ( x ). Từ đó suy ra tập nghiệm của ( 1 ) .
Bất phương trình chứa ẩn ở mẫu

Chú ý : Không nên qui đồng và khử mẫu .
Bất phương trình chứa ẩn trong dấu GTTĐ
∙ Tương tự như giải pt chứa ẩn trong dấu GTTĐ, ta hay sử dụng định nghĩa và đặc thù của GTTĐ để khử dấu GTTĐ .
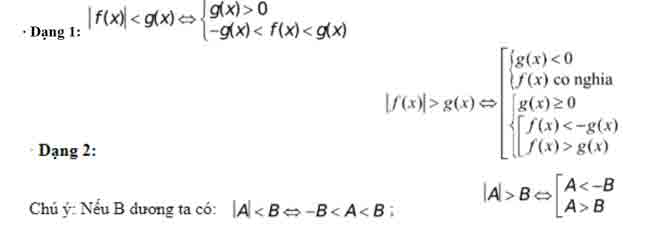
Bất phương trình quy về bậc hai:
Dấu của tam thức bậc hai

Bất phương trình bậc hai một ẩn ax2 + bx + c > 0 (hoặc ≥ 0; < 0; ≤ 0)
Để giải BPT bậc hai ta vận dụng định lí về dấu của tam thức bậc hai .
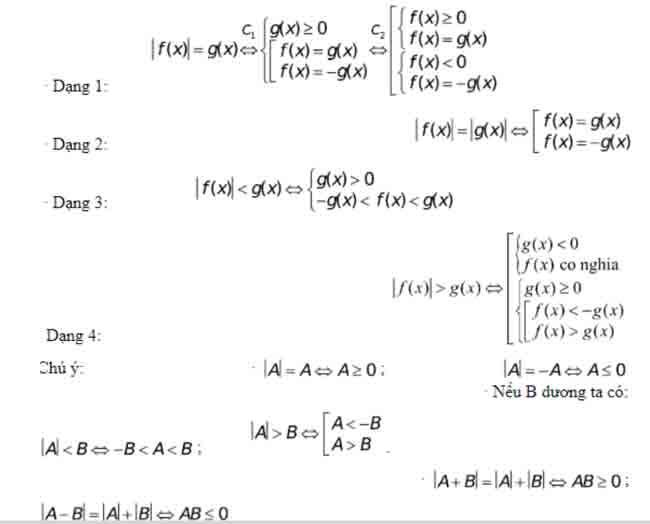
Phương trình – Bất phương trình chứa ẩn trong dấu GTTĐ
Để giải phương trình, bất phương trình chứa ẩn trong dấu GTTĐ, ta thường sử dụng định nghĩa hoặc đặc thù của GTTĐ để khử dấu GTTĐ .
Phương trình – Bất phương trình chứa ẩn trong dấu căn
Trong các dạng toán thì bất phương trình chứa căn được xem là dạng toán khó nhất. Để giải phương trình, bất phương trình chứa ẩn trong dấu căn ta cầ sử dụng kết hợp các công thức giải bất phương trình lớp 10 kết hợp với phép nâng luỹ thừa hoặc đặt ẩn phụ để khử dấu căn.

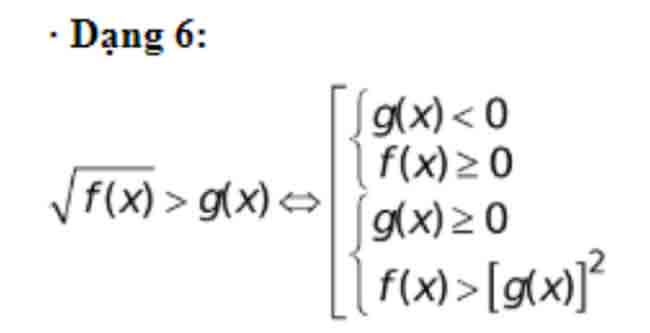
Bài tập giải bất phương trình lớp 10
1. Bài tập về Bất Phương Trình:
Bài 1/ BPT bậc nhất
1.1. Giải các bất phương trình sau:
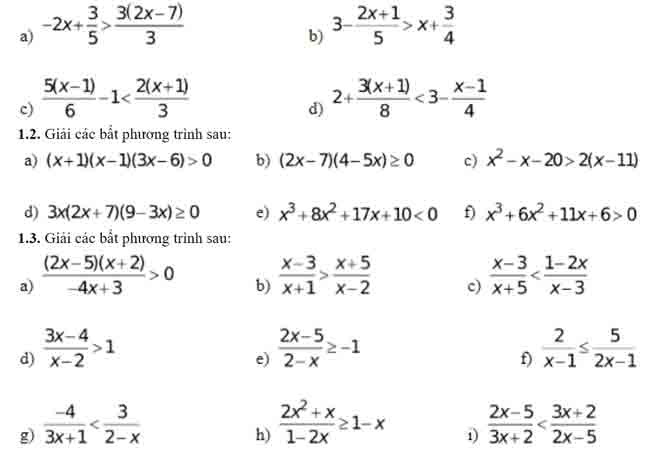
Bài 2/ BPT qui về bậc nhất
Giải những bất phương trình sau :
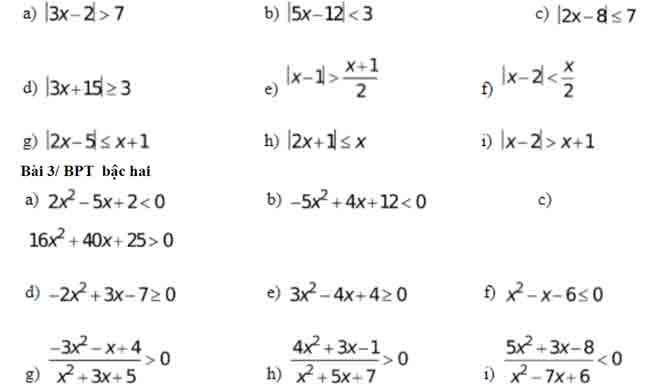
Bài 4/ BPT qui về bậc hai có chứa dấu GTTĐ
Giải những bất phương trình sau :

Bài 5/ BPT qui về bậc hai có chứa căn thức
Giải những phương trình sau :

2. Bài tập về Phương Trình
Bài 1: Giải các phương trình sau: (nâng luỹ thừa)



3. Bài tập tổng hợp các dạng:









Các dạng phương trình chứa căn, bất phương trình chứa căn cơ bản
Có khoảng chừng 4 dạng phương trình chứa căn, bất phương trình chứa căn cơ bản đó là

Một số ví dụ về phương trình và bất phương trình chứa căn thức
Ví dụ 1. Giải phương trình






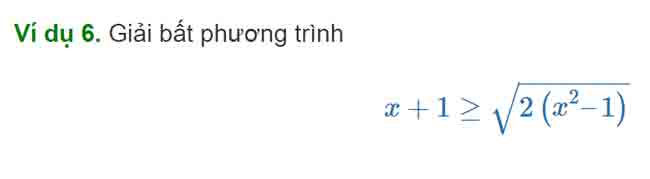





Ví dụ 10. Giải bất phương trình


Công thức bất phương trình chứa căn
Một số công thức biến đổi tương đương bất phương trình chứa căn


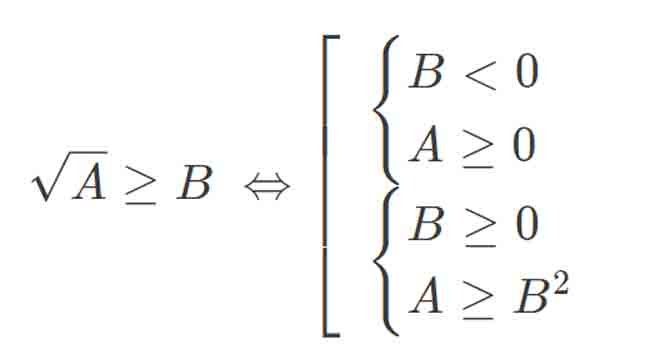
Việc kiểm soát và điều chỉnh vị trí những dấu bằng hoàn toàn có thể còn tạo ra công thức khác nữa. Tuy nhiên, với 4 công thức trên đây là đủ để ta giải những bất phương trình vô tỉ cơ bản .
Tóm tại, ta có 4 công thức đổi khác cơ bản sau cần nhớ :
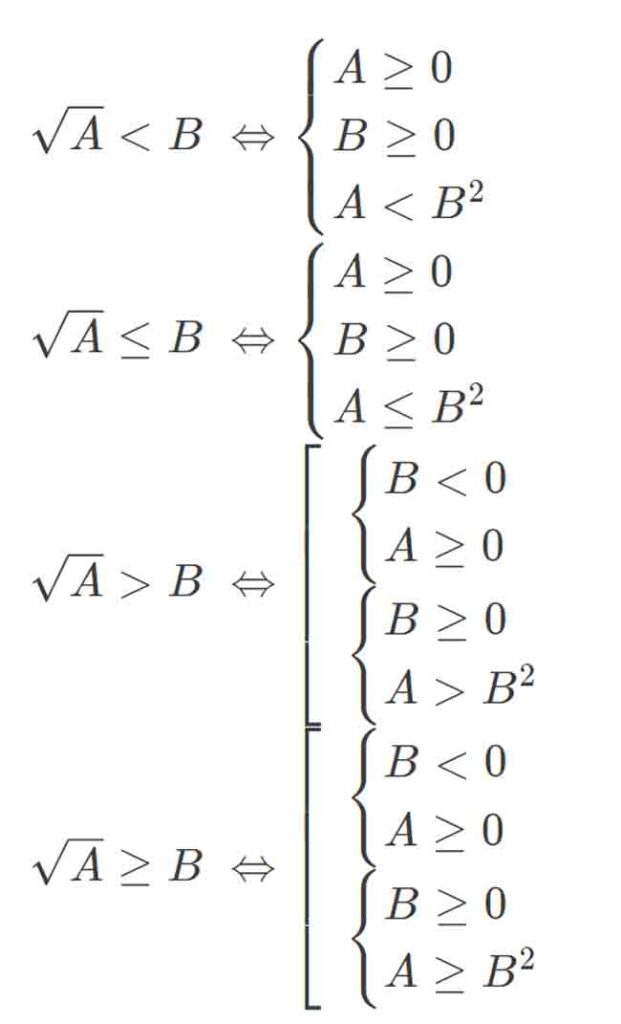
BÀI TẬP
Bài 1. Giải những bất phương trình
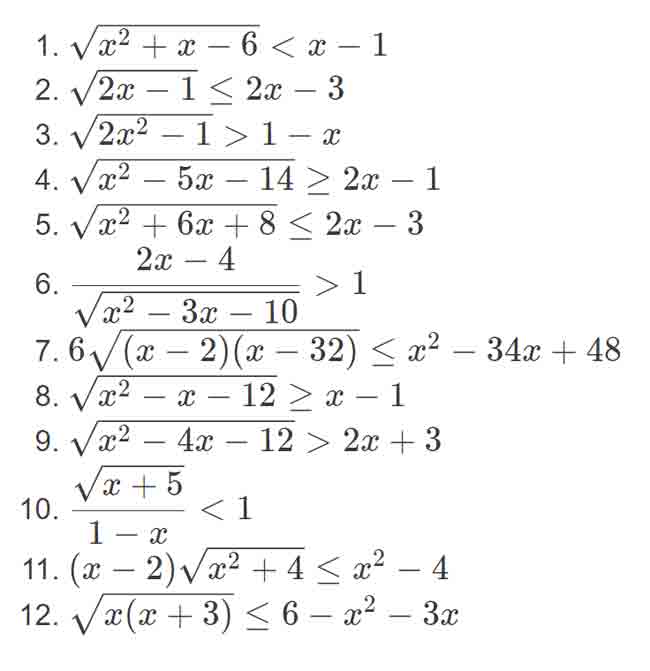
Bất phương trình một ẩn
° Bất phương trình một ẩn là một mệnh đề chứa biến có một trong các dạng: f(x)>g(x), f(x)
° Giá trị x0 thỏa mãn điều kiện xác định làm cho f(x0)
Điều kiện xác định của bất phương trình
° Điều kiện xác lập của bất phương trình là điều kiện kèm theo biến số x để những biểu thức f ( x ), g ( x ) có nghĩa .

Bất phương trình chứa tham số
° Trong bất phương trình, ngoài ẩn số còn hoàn toàn có thể có tham số được xem như hằng số. Giải biện luận phương trình chứa tham số là xét xem với những giá trị nào của tham số để bất phương trình vô nghiệm hoặc có nghiệm, tìm những nghiệm đó .
* Ví dụ: (2m-5)x + 8 > 0; x2 -mx + 2m – 1 ≤ 0. là các bất phương trình ẩn x tham số m.
Hệ bất phương trình một ẩn
° Việc tìm tập hợp những nghiệm chung của một tập hợp những bất phương trình một ẩn, ký hiệu :

° Giải hệ bất phương trình bằng cách tìm giao những tập hơp nghiệm của bất phương trình của hệ .
Bất phương trình tương đương
° Hai bất phương trình f1 ( x ) < g1 ( x ) và f2 ( x ) < g2 ( x ) được gọi là tương tự, ký hiệu : f1 ( x ) < g1 ( x ) ⇔ f2 ( x ) < g2 ( x ) nếu chúng có cùng một tập hợp nghiệm .
° Định lý: Goi D là điều kiện xác định của bất phương trình f(x) < g(x), h(x) là biể thức xác định với mọi x ∈ D thì:
i ) f ( x ) + h ( x ) < g ( x ) + h ( x ) ⇔ f ( x ) < g ( x ) . Hệ quả :
f(x) < g(x) + p(x) ⇔ f(x) – g(x) < p(x)
ii ) f ( x ). h ( x ) < g ( x ). h ( x ) ⇔ f ( x ) < g ( x ) nếu h ( x ) > 0 với mọi x ∈ D .
f ( x ). h ( x ) < g ( x ). h ( x ) ⇔ f ( x ) > g ( x ) nếu h ( x ) < 0 với mọi x ∈ D.
Bài tập về bất phương trình, hệ bất phương trình một ẩn
* Bài 1 trang 87 SGK Đại Số 10: Tìm các giá trị x thỏa mãn điều kiện của mỗi bất phương trình sau:







Source: https://futurelink.edu.vn
Category: Tin tổng hợp