Công thức logarit tổng hợp lớp 12 – Toán Thầy Định

Bởi

Chúng ta có những công thức logarit nào?. Việc nhớ được các công thức có ý nghĩa vô cùng quan trọng trong việc học chương lôgarit. Trong công thức lôgarit, có những công thức được suy ra từ công thức khác. Vì vậy chúng ta nên nhớ những công thức tổng quát. Rồi từ đó suy ra các công thức khác. Sau một thời gian luyện tập với cách như vậy kết hợp với làm bài tập, tôi cam đoan các bạn sẽ thuộc lòng các công thức. Bây giờ hãy đọc bài viết dưới đây để biết thêm nhé!

Để cho đỡ phải nhắc lại nhiều lần, trong các công thức dưới đây ( nếu không nói gì thêm ) tất cả chúng ta đều hiểu là các biểu thức có nghĩa. Tức là cơ số luôn dương, khác 1 và biểu thức dưới dấu logarit luôn dương .

I. LOGARIT LÀ GÌ

Logarit là đối ngược với mũ. Hay nói cách khác, nếu chúng ta lấy logarit của một số sẽ trả về số mũ với cùng cơ số.

Chúng ta cùng xét một ví dụ đơn thuần sau. Nếu ta lấy lũy thừa 3 của 2 thì ta có 2 ³ = 8. Điều đó có nghĩa là nếu ta lấy logarit cơ số 2 của 8 thì ta sẽ được hiệu quả là số 3 .
Tổng quát tất cả chúng ta có công thức sau :

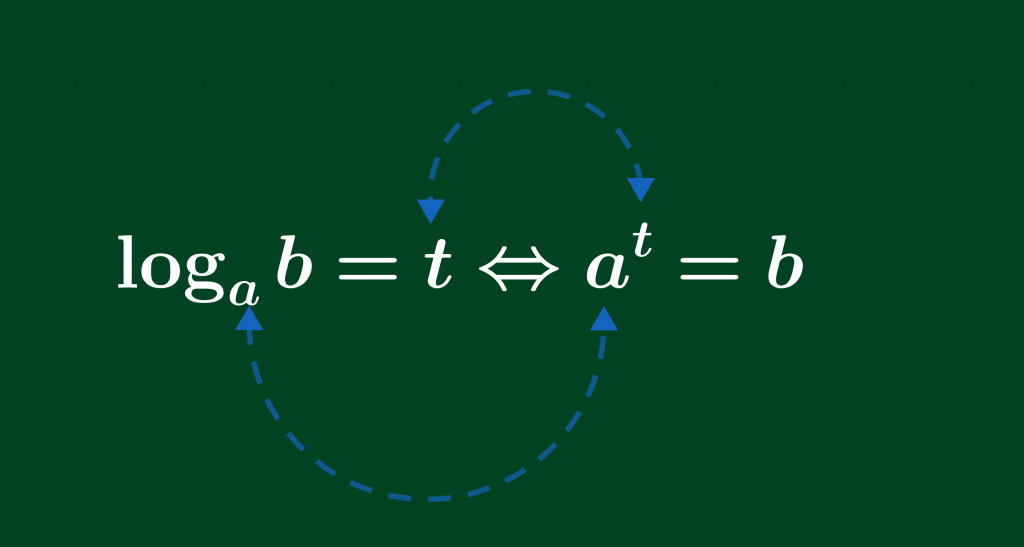
cách tính logarit

Cách tính logarit cơ số a của b theo định nghĩa .

Với nhiều người thì công thức này đơn giản rồi. Nhưng cũng có một số người sẽ không phân biệt được vị trí của a, b, t. Để khắc phục ta hãy nhớ “cơ số vẫn mãi là cơ số” và hình dung sơ đồ như ảnh trên. Khi nhớ được công thức này rồi ta hãy thử xem từ công thức này có suy ra thêm công thức nào nhé. Đầu tiên ta thay t bằng logarit cơ số a của b ở đẳng thức bên phải.

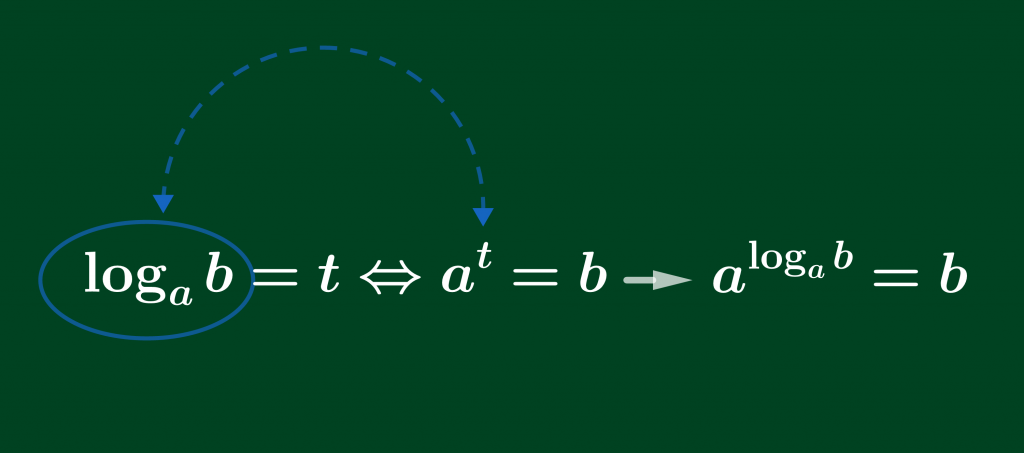
coông thức logarit

Dễ hiểu đúng không nào!

Tiếp tục từ công thức vừa tìm được thay b bằng 1 ta được công thức mới.

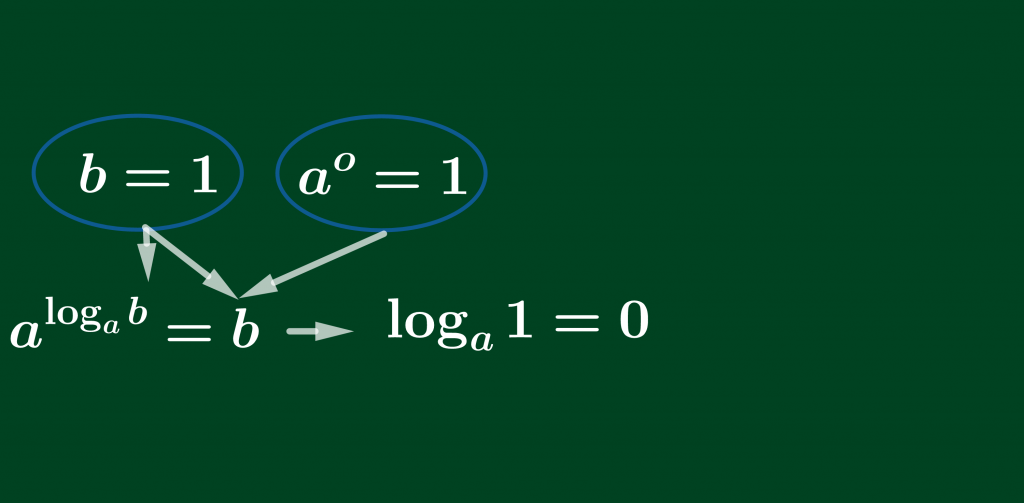
cong thuc logarit

II. BẢNG TỔNG HỢP CÁC CÔNG THỨC LOGARIT

Bảng dưới đây tổng hợp các công thức :
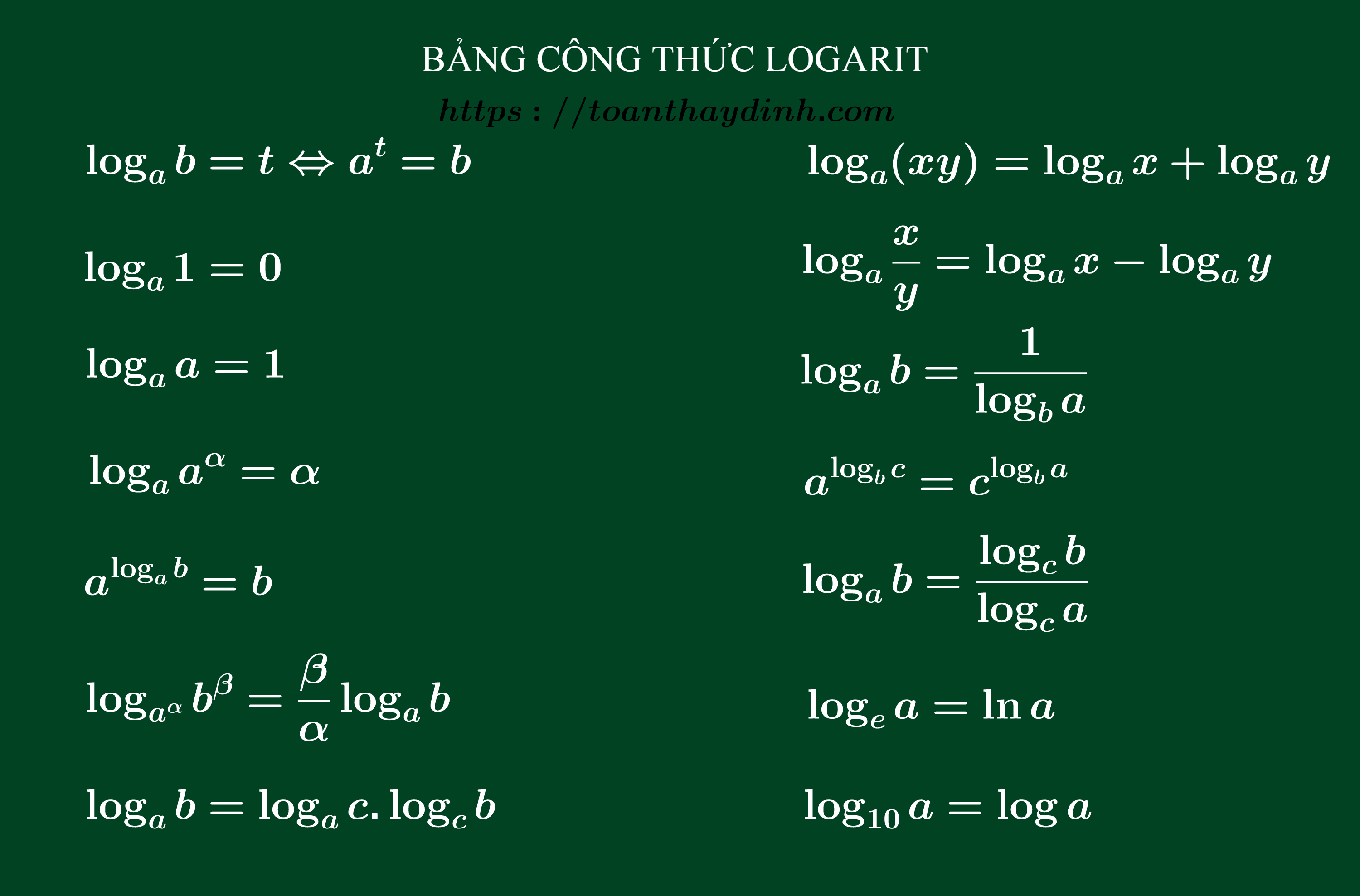
công thức logarit cơ bản
Trên đây là các công thức loogarit mà tôi đã trình làng đến các bạn. Chúc các bạn học tập tốt và thành công xuất sắc !

Xem thêm:

Hàm số logarit

Phương trình logarit thường gặp và phương pháp giải

Cách giải phương trình logarit bằng máy tính

Bất phương trình logarit tổng hợp

Tập xác định của hàm số mũ lũy thừa lôgarit