Công thức đạo hàm là kiến thức cơ bản của lớp 11 nếu không nắm được định nghĩa và bảng công thức đạo hàm thì không thể giải được bài tập. Vì vậy, chúng tôi sẽ chia sẻ lý thuyết định nghĩa, công thức tính đạo hàm bậc cao, đạo hàm log, đạo hàm gốc x, đạo hàm bậc ba, đạo hàm logarit, đạo hàm lượng giác, đối số đạo hàm giá trị tuyệt đối và nguyên hàm, .. chi tiết trong bài viết dưới đây để các bạn tham khảo với Mobitool nhé.
Video công thức đạo hàm
Tổng hợp công thức đạo hàm đầy đủ

Quy tắc cơ bản của đạo hàm
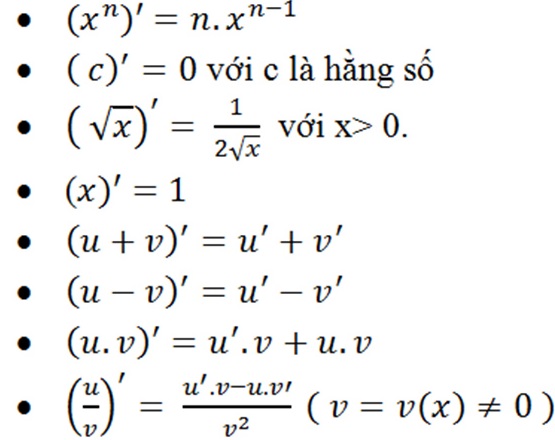
Bảng đạo hàm lượng giác

Tham khảo thêm:
- Cách tìm ma trận nghịch đảo 2×2,3×3,4×4 bằng máy tính Fx570 Es Plus
- Công thức lượng giác và các dạng bài tập liên quan
Công thức đạo hàm logarit
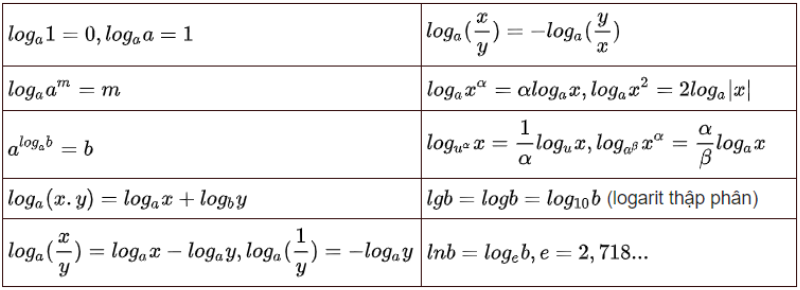
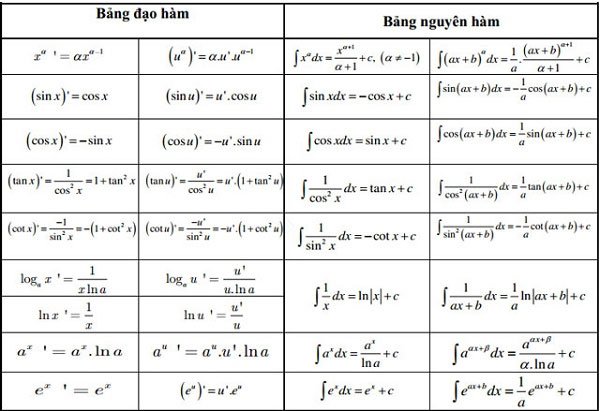
Công thức đạo hàm số mũ

công thức đạo hàm log
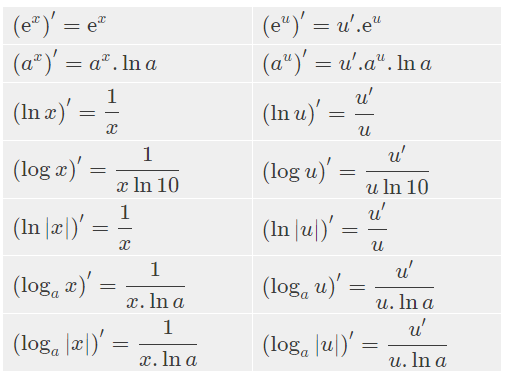
Bảng đạo hàm và nguyên hàm
Các dạng bài toán liên quan đến công thức đạo hàm
Dạng 1. Tính đạo hàm bằng định nghĩa
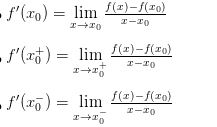
Hàm số y = f ( x ) có đạo hàm tại điểm x = x0 < => f ‘ ( x0 + ) = f ‘ ( x0 – ) Hàm số y = f ( x ) có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó. Ví dụ 1 : f ( x ) = 2 × 3 + 1 tại x = 2
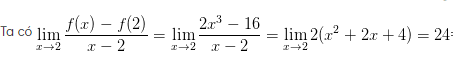
=> f ‘ ( 2 ) = 24
Dạng 2: Chứng minh các đẳng thức về đạo hàm
Ví dụ 1 : Cho y = e − x.sinx, chứng tỏ hệ thức y ” + 2 y ′ + 2 y = 0 Bài giải : Ta có y ′ = − e − x.sinx + e − x.cosx y ′ = − e − x.sinx + e − x.cosx y ” = e − x.sinx − e − x.cosx − e − x.cosx − e − x.sinx = − 2 e − x.cosx
Vậy y”+ 2y′+ 2y = −2.e−x.cosx− −2.e−x.sinx + 2.e−x.cosx + 2.e−x.sinx =0
Dạng 3: Viết phương trình tiếp tuyến khi biết tiếp điểm
Phương trình tiếp tuyến của đường cong ( C ) : y = f ( x ) tại tiếp điểm M ( x0 ; y0 ) có dạng : Ví dụ : Cho hàm số y = x3 + 3 mx2 + ( m + 1 ) x + 1 ( 1 ), m là tham số thực. Tìm những giá trị của m để tiếp tuyến của đồ thị của hàm số ( 1 ) tại điểm có hoành độ x = – 1 đi qua điểm A ( 1 ; 2 ). Tập xác lập D = R y ’ = f ‘ ( x ) = 3 × 2 + 6 mx + m + 1 Với x0 = – 1 => y0 = 2 m – 1, f ‘ ( – 1 ) = – 5 m + 4 Phương trình tiếp tuyến tại điểm M ( – 1 ; 2 m – 1 ) : y = ( – 5 m + 4 ) ( x + 1 ) + 2 m – 1 ( d ) Ta có A ( 1 ; 2 ) ∈ ( d ) < => ( – 5 m + 4 ). 2 + 2 m – 1 = 2 => m = 5/8
Dạng 4: Viết phương trình tiếp khi biết hệ số góc
Viết PTTT Δ của ( C ) : y = f ( x ), biết Δ có thông số góc k cho trước Gọi M ( x0 ; y0 ) là tiếp điểm. Tính y ’ => y ‘ ( x0 ) Do phương trình tiếp tuyến Δ có thông số góc k => y ’ = ( x0 ) = k ( i ) Giải ( i ) tìm được x0 => y0 = f ( x0 ) => Δ : y = k ( x – x0 ) + y0
Lưu ý:Hệ số góc k = y'( x0) của tiếp tuyến Δ thường cho gián tiếp như sau:
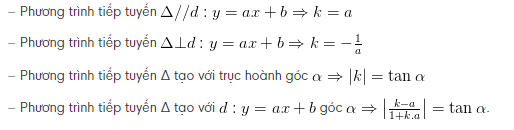
Ví dụ : Cho hàm số y = x3 + 3 × 2-9 x + 5 ( C ). Trong tổng thể những tiếp tuyến của đồ thị ( C ), hãy tìm tiếp tuyến có thông số góc nhỏ nhất. Ta có y ’ = f ‘ ( x ) = 3 × 2 + 6 x – 9 Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f ‘ ( x0 ) = 3 x02 + 6 x0 – 9 Ta có 3 x02 + 6 x0 – 9 = 3 ( x02 + 2 × 0 + 1 ) – 12 = 3 ( x0 + 1 ) 2 – 12 > – 12
Vậy min f( x0)= – 12 tại x0 = -1 => y0=16
Suy ra phương trình tiếp tuyến cần tìm : y = – 12 ( x + 1 ) + 16 < => y = – 12 x + 4
Dạng 5: Phương trình và bất phương trình có đạo hàm

Hy vọng với những kỹ năng và kiến thức về công thức đạo hàm mà chúng tôi vừa san sẻ hoàn toàn có thể giúp những bạn củng cố lại kiến thức và kỹ năng của mình để vận dụng giải những bài tập nhé
Source: https://futurelink.edu.vn
Category: Tin tổng hợp