Trong chương trình toán học lớp 8, định lý talet cùng những nội dung liên quan là phần kiến thức quan trọng yêu cầu học sinh cần nắm vững để giải các bài toán. Bài viết dưới đây của DINHNGHIA.VN sẽ giúp bạn tổng hợp những kiến thức hữu ích về chủ đề định lý talet, cùng tìm hiểu nhé!.
Tỉ số hai đoạn thẳng là gì?
Lý thuyết về tỉ số hai đoạn thẳng
Tỉ số của hai đoạn thẳng được định nghĩa là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng AB và CD sẽ được kí hiệu là \ ( \ frac { AB } { CD } \ )
Đoạn thẳng tỉ lệ: Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu như có tỷ lệ thức:
\(\frac{AB}{CD}=\frac{A’B’}{C’D’}\) hay \(\frac{AB}{A’B’}=\frac{CD}{C’D’}\)
Định lý Talet trong tam giác
Định lý Talet thuận trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác và cũng cắt hai cạnh còn lại thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ .
\ ( B’C ’ \ parallel BC \ Leftrightarrow \ frac { AB ’ } { AB } = \ frac { AC ’ } { AC }, \ frac { BB ’ } { AB } = \ frac { CC ’ } { AC }, \ frac { AB ’ } { BB ’ } = \ frac { AC ’ } { CC ’ } \ )

Định lý Talet đảo trong tam giác
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ABC nếu:
\(\frac{AB’}{AB}=\frac{AC’}{AC}\)
\(\frac{AB’}{BB’}=\frac{AC’}{CC’}\)
\(\frac{BB’}{AB}=\frac{CC’}{AC}\)
=> \(a//BC\)
Hệ quả của định lí Talet là gì?
Nếu một đường thẳng cắt hai cạnh ( hoặc cắt phần lê dài của hai cạnh ) của một tam giác và cũng song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho .
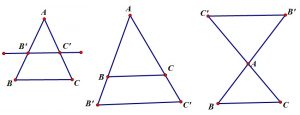
=> \ ( \ frac { AB ’ } { AB } = \ frac { AC ’ } { AC } = \ frac { B’C ’ } { BC } \ )
Định lí Talet trong hình thang
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
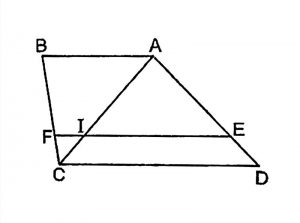
Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC
Nếu EF // AB // CD, ta có \(\frac{AE}{DE}=\frac{BF}{CF}\)
Ngược lại, nếu: \(\frac{AE}{DE}=\frac{BF}{CF}\) => EF // AB// CD
Ví dụ : Cho hình thang ABCD (AB // CD) AB < CD. Đường thẳng MN // với 2 đáy cắt cạnh AD, BC lần lượt tại M và N. Biết AD = 2cm, AM = 3cm, BC = 6cm. Tìm độ dài BN.
Giải: Vì hình thang ABCD có AB // CD // MN
Theo định lý Talet trong hình thang ABCD ta có, \ ( \ Rightarrow \ frac { AM } { AD } = \ frac { BN } { BC } \ Rightarrow BN = \ frac { AM.BC } { AD } = \ frac { 3.6 } { 2 } = 9 \ )
Trên đây là tổng hợp kiến thức về Định lý Talet trong tam giác và định lý Talet trong hình thang. Nếu có bất kì băn khoăn hay thắc mắc gì các bạn để lại bình luận bên dưới, chúng mình sẽ giải đáp ạ. Cảm ơn các bạn ^^ Nếu thấy hay thì chia sẻ nha ^^
Xem thêm:
Chi tiết về định lý Talet, cùng tìm hiểu thêm qua bài giảng dưới đây nhé !
(Nguồn: www.youtube.com)
3.5
/
5
(
4
bầu chọn
)
Please follow and like us :
![]()
![]()
Source: https://futurelink.edu.vn
Category: Tin tổng hợp