PHƯƠNG PHÁP GIẢI TOÁN BẰNG HỆ PHƯƠNG TRÌNH
Bước 1 : Lập hệ phương trình
- Chọn 2 ẩn, chọn đơn vị và đặt điều kiện thích hợp cho hai ẩn. (Ẩn là các đjai lượng cần tìm)
- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
- Lập hệ phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2 : Giải hệ phương trình. Có thể vận dụng các chiêu thức để giải hệ phương trình như : giải pháp thế, chiêu thức công đại số hoặc dùng ẩn phụ nếu gặp bài toán phức tạp, …
Bước 3: Kiểm tra nghiệm của phương trình vừa giải và đưa ra kết luận
Bạn đang đọc: GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH
Ví dụ minh họa về chiêu thức giải lập hệ phương trìnhTỉ số của 2 số là 3 : 4. Nếu giảm số lớn đi 100 và tăng số nhỏ thêm 200 thì tỉ số mới là 5 : 3. Tìm 2 số đóGiải :Gọi số lớn là y, số bé là x ( y > x )Tỉ số của 2 số là 3 : 4 thì ta có x / y = 3 / 4 ( 1 )Nếu giảm số lớn đi 100 và tăng số bé lên 200 thì tỉ số mới là 5 : 3 như vậy ta có phương trình 🙁 x + 200 ) / ( y – 100 ) = 5 / 3 => 3 x – 5 y = – 1100 ( 2 )Giải hệ phương trình ( 1 ) và ( 2 ) tâ được nghiệm x = 300, y = 400Vậy 2 số cần tìm là x = 300, y = 400
CÁC DẠNG TOÁN GIẢI BẰNG HỆ PHƯƠNG TRÌNH
Bài toán về quan hệ giữa các số
Phương pháp giải bài toán về quan hệ giữa các số
- Tổng của a và b là m thì ta có a + b = m
- Số a lớn hơn số b là m thì ta có a – b = m
- Số a bằng k lần số b thì ta có a = k.b
Ví dụ minh họa
Ví dụ1 : một thửa ruộng hình chữ nhật nếu tăng chiều dài thêm 2 m và tăng chiều rộng thêm 3 m thì diện tích quy hoạnh tăng thêm 100 mét vuông. Nếu giảm chiều dài và chiều rộng đi 2 m thì diện tích quy hoạnh thì diện tích quy hoạnh giảm đi 68 mét vuông. Tính diện tích quy hoạnh của thừa ruộng đó .Giải :Gọi chiều dài thửa ruộng là x ( x, m > 0 ) và chiều rộng là y ( m, y > 0 ) .Nếu tăng chiều dài thêm 3 m và tăng chiều rộng thêm 2 m thì diện tích quy hoạnh tăng 100 mét vuông như vậy ta có được phương trình sau 🙁 x + 2 ). ( y + 3 ) = xy + 100 => 3 x + 2 y = 94 ( 1 )Nếu giảm chiều dài và chiều rộng đi 2 m thì diện tích quy hoạnh giảm đi 68 mét vuông ta có được phương trình tương ứng như sau( x + 2 ). ( y + 3 ) = xy – 68 => – 2 x – 2 y = – 72 ( 2 )Giải hệ phương trình ( 1 ) và ( 2 ) ta được nghiệm x = 22 và y = 14 ( thỏa mãn nhu cầu điều kiện kèm theo )Vậy diện tích quy hoạnh thửa ruộng là 22. 14 = 308 mét vuôngVí dụ 2 : Tháng thứ nhất hai tổ sản xuất được 900 chi tiết cụ thể máy. Tháng thứ hai tổ I vượt mức 15 % và tổ II vượt mức 10 % so với tháng thứ nhất. Vì vậy hai tổ đã sản xuất được 1010 chi tiết cụ thể máy. Hỏi tháng thứ nhất mỗi tổ sản xuất được bao nhiêu cụ thể máy ?Giải :Gọi số chi tiết cụ thể máy của tổ I sản xuất được trong tháng thứ nhất là x ( cụ thể, x thuộc số tự nhiên )Gọi số chi tiết cụ thể máy của tổ II sản xuất được trong tháng thứ nhất là y ( cụ thể, y thuộc số tự nhiên )Tháng thứ nhất cả 2 tổ sản xuất được 900 cụ thể máy từ đó ta lập được phương trình ( 1 ) như sau :X + y = 900Tháng thứ hai tổ I vượt 15 % và tổ II vượt 10 % nên đã sản xuất được 1010 chi tiết cụ thể máy từ đó ta lập được phương trình ( 2 ) như sau :115 x / 100 ) + ( 110 y / 100 ) = 1010Giải hệ phương trình ( 1 ) và ( 2 ) ta có được nghiệm là x = 400 và y = 500 ( thỏa mãn nhu cầu điều kiện kèm theo )Vây đáp án là trong tháng thứ nhất tổ I đã sản xuất được 400 chi tiết cụ thể máy và tổ II đã sản xuất được 500 cụ thể máyVí dụ 3 : Hai kho chứa 45 tấn hàng. Nếu chuyển 50 tấn từ kho I sang kho II thì số hàng kho II bằng 4 / 5 số hàng kho I. Tính số hàng trong mỗi khoGiải :Gọi số hàng trong kho I là x ( tấn, x > 0 ), số hàng trong kho II là y ( tấn, y > 0 )Hai kho chứa 450 tấn hàng nên ta có phương trình ( 1 ) 😡 + y = 455Nếu chuyển 50 tấn từ kho I sang kho II thì số hàng kho II bằng 4 / 5 số hàng kho I nên ta có được phương trình ( 2 ) : y + 50 = 4/5 ( x – 50 )Giải hệ phương trình ( 1 ) và ( 2 ) ta được nghiệm x = 300 và y = 150, hai nghiệm đều thỏa mãn nhu cầu điều kiện kèm theoVậy số hàng trong kho I là 300 tấn hàng và số hàng trong kho II là 150 tấn hàng
Dạng toán liên quan đến chữ số
Phương pháp giải dạng toán liên quan đến chữ số
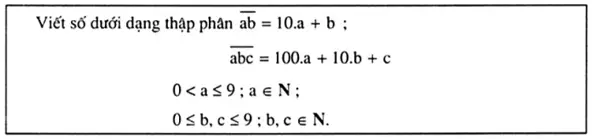
Ví dụ minh họa
Ví dụ 1 : Tìm số tự nhiên có 2 chữ số biết rằng tổng các chữ số của nó bằng 10 và nếu viết số đó theo thứ tự ngược lại thì được số mới nhỏ hơn số bắt đầu 18 đơn vị chức năngGiảiGọi chữ số hàng chục là x, chữ số hàng đơn vị chức năng là y với điều kiện kèm theo x > 0, y nhỏ hơn hoặc bằng 9, cả x và y đều thuộc số tự nhiên

Ví dụ 2 : một số ít tự nhiên có 2 chữ số. Tỉ số giữa chữ số hàng chục và chữ số hàng đơn vị chức năng là 2 / 3. Nếu viết thêm chữ số 1 xen vào giữa thì được số mới lớn hơn số đã cho là 370 đơn vị chức năng. Tìm số đã cho .

Dạng toán làm chung công việc
Phương pháp giải:
- Toán làm chung công việc có ba đại lượng tham gia là toàn bộ công việc, phần việc trong một đơn vị thời gian và thời gian
- Nếu một đội làm xong công việc trong x ngày thì một ngày đội đó làm được 1 / x công việc
- Xem toàn bộ công việc là 1
Ví dụ minh họa
Ví dụ 1 : Hai công nhân cùng làm một việc làm trong 18 h thì xong. Nếu người thứ nhất làm 6 h và người thứ hai làm 12 h thì chỉ hoàn thành xong 50 % việc làm. Hỏi nếu làm riêng thì mỗi người hoàn thành xong việc làm đó trong bao lâu ?GiảiGọi thời hạn người thứ nhất làm một mình đến khi hoàn thành xong việc làm là x ( giờ, x > 0 )Gọi y là thời hạn người thứ nhất làm một mình đến khi hoàn thành xong việc làm ( giờ, y > 0 )Trong 1 h người thứ nhất làm được 1 / x việc làm. Người thứ hai làm được 1 / y việc làmHai người làm chung 18 h thì xong vậy ta có phương trình ( 1 ) :1 / x + 1 / y = 1 / 18Nếu người thứ nhất làm 6 h và người thứ hai làm trong 12 h thì triển khai xong 50 % việc làm nhưu vậy ta có được phương trình ( 2 ) :6 / x + 12 / y = 50 %Giải hệ phuwogn trình ( 1 ) và ( 2 ) ta thu được nghiệm x = 36 và y = 36, hai nghiệm thỏa mãn nhu cầu điều kiện kèm theo đã choNhư vậy nếu làm riêng thì người thứ nhất hoàn thành xong việc làm trong 36 h và người thứ hai triển khai xong việc làm trong 36 hVí dụ 2 : Hai vòi nước chảy cùng vào một bẻ không có nước thì sau 1 h30 phút sẽ đầy bể. Nếu mở vòi thứ I chảy trong 15 phút rồi khóa lại và mở vòi thứ II chảy trong 20 phút thì được 1 / 5 bể. Hỏi nếu mỗi vòi chạy riêng thì bao lâu bể đầy ?Giải :Ta có : 1 h30 phút = 3/2 h ; 15 phút = 1/4 h ; 20 phút = 1/3 hGọi thời hạn vòi I chảy một mình đầy bể là x ( giờ, x > 0 )Gọi thời hạn vòi II chảy một mình đầy bể là y ( giờ, y > 0 )Hai vòi cùng chảy thì sau 1 h30 phút bể sẽ đầy nước từ đó ta có phương trình ( 1 ) :1 / x + 1 / y 2/3Vòi I chảy trong 15 phút và voi II chảy trong 20 phút thì được 1/5 bể từ đó ta có được phương trình ( 2 ) :1/4 x + 1/3 y = 1/5Giải hệ phương trình ( 1 ) và ( 2 ) ta thu được nghiệm x = 15/4 và y = 5/2, hai nghiệm thỏa mãn nhu cầu điều kiện kèm theo bài cho .Vậy nếu chảy riêng từng vòi thì vòi I chảy đầy bể trong 15/4 giờ, vòi II chảy đầy bể trong 5/2 giờ
Dạng toán chuyển động
Phương pháp giải
- Toán chuyển động có ba đai lượng tham gia: vận tốc (v), thời gian (t), quãng đường (s)
- Công thức: v = s /t ; s = v.t ; t = s/v
ví dụ minh họa
Ví dụ 1 : một ca nô đi từ A đến B với tốc độ và thời hạn dự tính. Nếu ca nô tăng tốc độ lên thêm 3 km / h thì thời hạn rút ngắn được 2 giờ. Nếu ca nô giảm tốc độ đi 3 km / giờ thì thười gian tăng lên 3 h. Tính tốc độ và thười gian dự tính của ca nô .Giải :Gọi tốc độ dự tính của ca nô là x ( km / h ; x > 3 ) và thời hạn dự tính đi từ A đến B là y ( giờ, y > 0 )Nếu ca nô tăng tốc độ thêm 3 km / h thì thười gian rút ngắn được 2 giờ như vậy ta có được phương trình ( 1 ) 🙁 x + 3 ). ( y-2 ) = xyNếu ca nô giảm tốc độ thêm 3 km / h thì thời hạn tăng thêm 3 giờ từ đó ta có phương ( trình ( 2 ) 🙁 x – 3 ). ( y + 3 ) = xyGiải hệ phương trình ( 1 ) và ( 2 ) ta thu được nghiệm là x = 15 và y = 12, nghiệm thu sát hoạch được thỏa mãn nhu cầu điều kiện kèm theo đã choVậy tốc độ dự tính của ca nô là 15 km / hVà thời hạn dự tính của ca nô là 12 hVí dụ 2 : Một ca nô chảy trên sông trong 8 giờ xuôi dòng được 81 km và ngược dòng 105 km. Một lần khác ca nô chạy trên sông trong 4 giờ xuôi dòng 54 km và ngược dòng 42 km. Tính tốc độ riêng của ca nô và tốc độ dòng nước. Biết tốc độ riêng của ca nô và tốc độ dòng nước không đổiGiải :Gọi tốc độ riêng của ca nô là x ( km / h, x > 0 )Vận tốc dòng nước là y ( km / h, x > y > 0 )Suy ra tốc độ xuôi dòng của ca nô là : ( x + y ) km / h và tốc độ ngược dòng của ca nô là ( x – y ) ( km / h )Ca nô chảy trên sông trong 8 giờ xuôi dòng được 81 km và ngược dòng 105 km, ta có phương trình ( 1 ) :81 / ( x + y ) + 105 / ( x – y ) = 8Ca nô chạy trên sông trong 4 giờ xuôi dòng 54 km và ngược dòng 42 km, ta có phương trình ( 2 ) :54 / ( x + y ) + 42 / ( x – y ) = 4Giải hệ phương trình ( 1 ) và ( 2 ) ta được nghiệm x = 24 và y = 3 thỏa mãn nhu cầu điều kiên đã choNhư vậy tốc độ riêng của ca nô là 24 km / h và tốc độ dòng nước là 3 km / h
Dạng toán có nội dung lý, hóa
Phương pháp giải
Nắm vững các công thức lí, hóa tương quan
ví dụ minh họa
Ví dụ 1 : Có hai loại quẳng chứa 75 % sắt và 50 % sắt. Tính khối lượng của mỗi loại quẳng đem trộn để được 25 tấn quẳng chứa 66 % sắt .GiảiGọi khối lượng loại quẳng chứa 75 % sắt và 50 % sắt lần lượt là x và y ( tấn, x > 0, y > 0 )Theo bài ra ta có hệ phương trình :X + y = 25
(75x/ 100) + (50y /100) = (66/ 100). 25
Giải hệ phương trình ta được x = 16 và y = 9, thỏa mãn nhu cầu điều kiện kèm theoVậy đem trộn 16 tấn loại quẳng chứa 75 % sắt và 9 tấn loại quẳng chứa 50 % sắt ta sẽ được 25 tấn quẳng chứa 66 % sắtVí dụ 2 : Người ta cho thêm 1 kg nước vào dung dịch A thì được dung dịch B có nồng độ axit là 20 %. Sau đó lại cho thêm 1 kg axit vào dung dịch B thì được dung dịch C có nồng độ axit là 33. ( 1/3 ) %. Tính nồng độ axit trong dung dịch AGiải :Gọi khối lượng axit trong dung dịch A là x ( kg, x > 0 )Gọi khối lượng nước trong dung dịch A là y ( kg, y > 0 )Cho thêm 1 kg nước vào dung A thì được dung dịch B có nồng độ axit là 20 %. Ta có được phương trình tương ứng là ( 1 ) như sau 😡 / ( x + y + 1 ) = 20 %Cho thêm 1 kg axit vào dung dịch B thì được dung dịch C có nồng độ axit là 33. ( 1/3 ) %. Ta được phương trình ( 2 ) 🙁 x + 1 ) / ( x + y + 2 ) = 33. ( 1/3 ) % .Giải hệ phương trình ( 1 ) và ( 2 ) ta được nghiệm x = 1, y = 3Vậy nồng độ axit trong dung dịch A là : 1 / ( 3 + 1 ) = 1 / 4 = 25 %
BÀI TẬP RÈN LUYỆN
Bài tập 1
Một otô du lịch đi từ A đến C. Cùng lúc từ khu vực B nằm trên đoạn AC có một oto vận tải đường bộ cùng đi đến C. Hỏi oto du lịch đi từ A đến B mất bao lâu, biết rằng tốc độ của oto tải bằng 3 / 5 tốc độ oto du lịchGiải :Gọi thời hạn oto du lịch đi từ A đến B là x ( h, 0 < x < 5 )Ta có thời hạn oto du lịch đi từ B đến C là 5 – x ( h )Vận tốc xe oto du lịch là ( BC / 5 – x ) km / hVì tốc độ của oto tải bằng 3 / 5 tốc độ của oto du lịch nên ta có phuơng trình :BC / 5 = ( 3 / 5 ). ( BC / x-5 )Giải phương trình ta được x = 2Vậy oto du lịch đi từ A đến B hết 2 ( h )
Bài tập 2
Mỗi vòi A, B khi mở chảy nước vào bể với lưu lượng đều. Nếu vòi A chảy trong 4 giờ và vòi B chảy trong 3 giờ thì nước trong bể là 55 lít. Nếu vòi A chảy trong 3 giờ và vòi B chảy trong 4 giờ thì nước trong bể là 57 lít. Vậy nếu hai vòi cùng chảy một lúc thì sau bao nhiêu lâu sẽ làm đầy bể ? Biết rằng dung tích của bể 320 lítGiải :Gọi x và y lần lượt là lượng nước chảy qua vòi A và B trong 1 giờVì vòi A chảy trong 4 giờ và vòi B chảy trong 3 giờ thì lượng nước trong bể là 55 lít nên ta có phương trình ( 1 ) :4 x + 3 y = 55Tương tự như vậy ta lại có vòi A chảy trong 4 giờ và vòi B chảy trong 3 giờ thì lượng nước trong bể là 55 lít nên ta có phương trình ( 2 ) :3 x + 4 y = 57Giải hệ phương trình ( 1 ) và ( 2 ) và được x = 7 và y = 9. Như vậy thời hạn để hai vòi A và B cùng chảy đầy bể là 320 / ( 9 + 7 ) = 20 giờ
Bài tập 3
Tính độ dài hai cạnh góc vuông của một tam giác vuông biết rằng nếu tăng mỗi cạnh lên 30 cm thì diện tích quy hoạnh tam giác đó sẽ tăng thêm 36 cm2 và nếu một cạnh giảm đi 2 cm, cạnh kia giảm đi 4 cm thì diện tích quy hoạnh tam giác giảm đi 16 cm2Giải :Gọi độ dài cạnh thứ nhất và cnahj thứ hai cần tìm lần lượt là a cm và b cm, với điều kiện kèm theo a > 2, b > 4. Khi đó diện tích quy hoạnh tam giác lá = ab cm2Khi tăng mỗi cạnh lên 30 cm thì diện tích quy hoạnh tam giác đó sẽ tăng thêm 36 cm2 nên ta có phương trình ( 1 ) 🙁 a + 3 ). ( b + 3 ) = ab + 36Nếu một cạnh giảm đi 2 cm, cạnh kia giảm đi 4 cm thì diện tích quy hoạnh tam giác giảm đi 16 cm2 nên ta có phương trình ( 2 ) : ( a – 2 ). 9 b – 4 ) = ab – 26Giải hệ phương trình ( 1 ), ( 2 ) ta được hiệu quả a = 3 và b = 6Vậy độ dài hai cạnh là 3 cm và 5 cm
Bài tập 4
Bài toán 5
Tính chiều dài và chiều rộng của mảnh đát hình chữ nhật bết rằng nếu tăng gấp đôi chiều dài và giảm đi 50% chiều rộng thì chu vi mảnh đất tăng lên 180 cm. Nếu tăng gấp đôi chiều rộng và giảm đi 50% chiều dài thì chu vi tăng lên 120 cmGiải :Gọi chiều dài và chiểu rộng của mảnh đất lần lượt là x ( m ), y ( m ) với điều kiện kèm theo x > 0 và y > 0. Khi đó chu vi mảnh đất là d = x + y ( m )Khi tăng gấp đôi chiều dài và giảm đi 50% chiều rộng thì chu vi mảnh đất tăng lên 180 cm nên 2 x + ( y / 2 ) = ( x + y ) + 180 ( 1 )Khi tăng gấp đôi chiều rộng và giảm đi 50% chiều dài thì chu vi tăng lên 120 cm nên ( x / 2 ) + 2 y = ( x + y ) + 120 ( 2 )Giải hệ phương trình ( 1 ) và ( 2 ) ta được hiệu quả thỏa mãn nhu cầu điều kiện kèm theo là x = 165 và y = 135. Vậy chiều dài của mảnh đất là 165 m và chiều rộng của mảnh đất là 135 m
Bài tập 6
Trong túi đượng bi đỏ và bi xanh. Nếu lấy ra một bi đỏ thì một phần bảy số bi còn lại là đỏ. Nếu lấy ra hai bi xanh thay vì một bi đỏ thì một phần năm số bi còn lại là đỏ. Hỏi trong túi lúc đầu có bao nhiêu bi xanh và bao nhiêu bi đỏGiải :Gọi số bi đỏ lúc đầu có trong túi là x, x > 1Gọi số bi xanh lúc đầu có trong túi là y, y > 2Nếu lấy ra một bi đỏ thì một phần bảy số bi còn lại là đỏ nên ta lập được phương trình ( 1 ) 🙁 x – 1 + y ). ( 1 / 7 ) = x – 1Nếu lấy ra hai bi xanh thay vì một bi đỏ thì một phần năm số bi còn lại là đỏ nên ta lập được phương trình ( 2 ) 🙁 x + y – 2 ). ( 1 / 5 ) = xGải hệ phương trình ( 1 ) và ( 2 ) ta được nghiệm x = 4 và y = 18Vậy trong túi lúc đầu có 4 bi đỏ và 18 bi xanh
Source: https://futurelink.edu.vn
Category: Tin tổng hợp