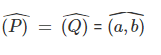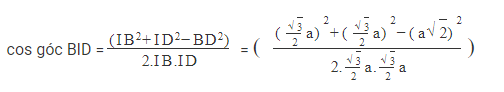Góc giữa 2 mặt phẳng song song, trùng nhau Toán Lớp 11, Lớp 12 ( kèm bài tập )
Góc giữa 2 mặt phẳng là nội dung rất quan trong trong phần kiến thức và kỹ năng giúp bạn lấy trọn điểm hình học ở bài thi tốt nghiệp. Bạn phải xác lập được góc giữa hai mặt phẳng mới hoàn toàn có thể xử lý được bài toán
Nhưng đừng lo, hãy theo dõi bài viết dưới đây. Chúng tôi sẽ giúp bạn chinh phục dạng toán này một cách nhanh gọn và đơn thuần
Góc giữa 2 mặt phẳng là gì ?
– Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó .
– Trong khoảng trống 3 chiều, góc giữa 2 mặt phẳng còn được gọi là ‘ góc khối ’, là phần khoảng trống bị số lượng giới hạn bởi 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng .
Cách xác định góc giữa 2 mặt phẳng
==> Để hoàn toàn có thể xác lập đúng mực góc giữa 2 mặt phẳng bạn vận dụng những cách sau :
Gọi P là mặt phẳng 1, Q là mặt phẳng 2
+) Trường hợp 1: Hai mặt phẳng (P), (Q) song song hoặc trùng nhau thì góc của 2 mặt phẳng bằng 0,
+) Trường hợp 2: Hai mặt phẳng (P), (Q) không song song hoặc trùng nhau.
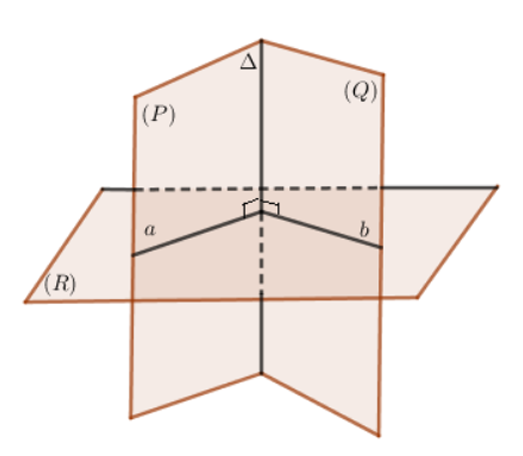
- Cách 1: Dựng 2 đường thẳng n và p vuông góc lần lượt với 2 mặt phẳng (P), (Q). Khi đó góc giữa 2 mặt phẳng (P), (Q) là góc giữa 2 đường thẳng n và p.
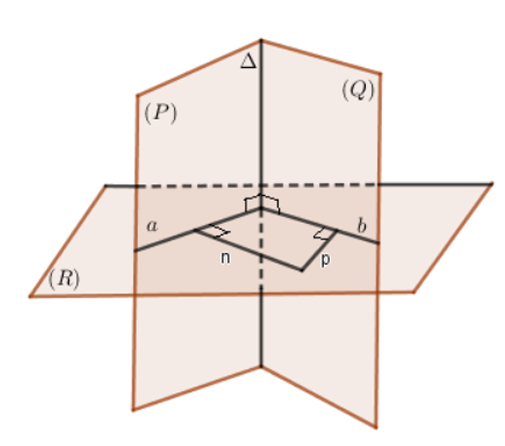
- Cách 2: Để xác định góc giữa 2 mặt phẳng đầu tiên bạn cần xác định giao tuyến Δ của 2 mặt phẳng (P) và (Q). Tiếp theo, bạn tìm một mặt phẳng (R) vuông góc với giao tuyến Δ của 2 mặt phẳng (P), (Q) và cắt 2 mặt phẳng tại các giao tuyến a, b.
==> Góc giữa 2 mặt phẳng (P), (Q) là góc giữa a và b.
Phương pháp tính góc giữa 2 mặt phẳng
==> Có 2 giải pháp bạn hoàn toàn có thể vận dụng để tính góc giữa 2 mặt phẳng :
+) Phương pháp 1: Sử dụng hệ thức lượng trong tam giác vuông, định lý hàm số sin, hàm số cos.
+) Phương pháp 2: Dựng mặt phẳng phụ (R) vuông góc với giao tuyến c mà (Q) giao với (R) = a, (P) giao với (R) = b.
===>
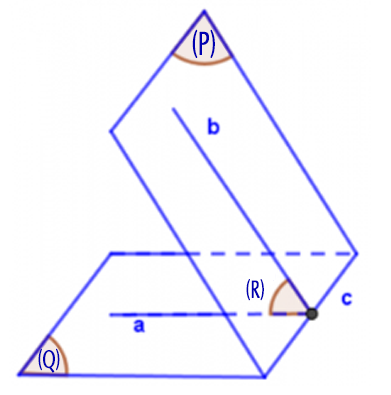
Bài tập minh họa góc giữa hai mặt phẳng
Bài tập 1: Cho hình chóp tứ giác đều S.ABCD có đáy là ABCD và độ dài các cạnh đáy bằng a, SA = SB = SC = SD = a. Tính cos góc giữa hai mặt phẳng (SAB) và (SAD).
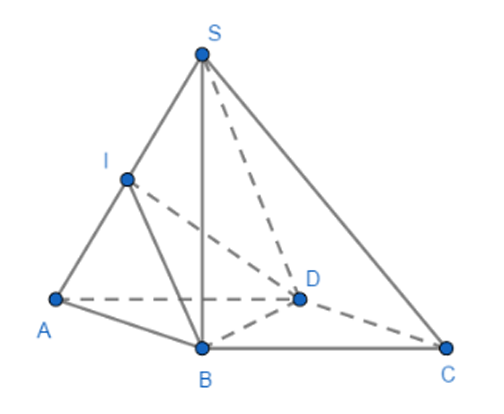
– Hướng dẫn giải:
Gọi I là trung điểm đoạn SA. Ta có tam giác SAD và tam giác SAB đều
Áp dụng định lý cosin vào tam giác BID ta được:
Suy ra góc ( ( SAB ), ( SAD ) ) = 1/3
Cám ơn bạn đã theo dõi bài viết này, kỳ vọng những nội dung chúng tôi san sẻ đến bạn sẽ là những thông tin có ích giúp bạn giải quyết và xử lý được yếu tố của mình nhé !
Source: https://futurelink.edu.vn
Category: Tin tổng hợp