1. GÓC GIỮA HAI MẶT PHẲNG
Định nghĩa : Góc giữa 2 mặt phẳng trong khoảng trống là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng đó .
Hình ảnh cánh cửa đang mở cho chúng ta hình dung về góc giữa 2 mặt phẳng.
Bạn đang đọc: Góc giữa hai mặt phẳng trong không gian – Toán Thầy Định
Theo đó :
- Góc giữa 2 mặt phẳng là một góc không tù.
- Góc giữa 2 mặt phẳng bằng 0º khi và chi khi 2 mặt phẳng đó song song hoặc trùng nhau.
- Góc giữa 2 mặt phẳng bằng 90º khi và chỉ khi 2 mặt phẳng đó vuông góc.
Tuy nhiên trong thực hành thực tế tính góc của 2 mặt phẳng thì ta không dùng định nghĩa trên. Đơn giản vì việc xác lập đường vuông góc với măt phẳng không phải khi nào cũng đơn thuần. Hơn thế nữa, xác lập góc giữa 2 đường thẳng lại là một yếu tố cũng không đơn thuần. Sau đây, tất cả chúng ta sẽ có 2 cách để xác lập góc giữa 2 mặt phẳng .
2. TÍNH GÓC GIỮA HAI MẶT PHẲNG BẰNG GÓC PHẲNG NHỊ DIỆN
Góc phẳng nhị diện là gì?
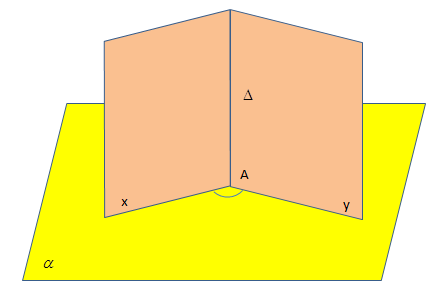
Cho hai nửa mặt phẳng chung bờ Δ. Mặt phẳng ( α ) bất kể vuông góc với Δ cắt hai nửa mặt phẳng theo 2 tia lần lượt là Ax và Ay. Khi đó góc được gọi là góc phẳng nhị diện tạo bởi hai nửa mặt phẳng nóí trên. Rõ ràng mặt phẳng ( α ) đổi khác là không tác động ảnh hưởng đến giá trị góc ∠ xAy .
Giả sử ( P ) và ( Q. ) là hai mặt phẳng lần lượt chứa hai mặt phẳng nói trên. Ta dễ thấy góc giữa ( P ) và ( Q. ) bằng hoặc bù với góc phẳng nhị diện. Cụ thể là bằng khi góc phẳng nhị diện không tù, và bù khi góc phẳng nhị diện tù .
Ứng dụng góc phẳng nhị diện vào tìm góc giữa mặt bên và mặt đáy của hình chóp
Để tìm góc giữa mặt bên và dưới mặt đáy của hình chóp ta hoàn toàn có thể thực thi như sau :
- Bước 1: Xác định hình chiếu của đỉnh S lên mặt đáy ( chân đường cao). Tạm gọi điểm này là A.
- Bước 2: Xác định giao tuyến của mặt bên và mặt đáy.
- Bước 3: Chiếu chân đường cao lên giao tuyến. Tạm gọi điểm này là M. Đó chính là đỉnh của góc cần tìm. Góc cần tìm là góc ∠SMA.
Ví dụ:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông tại B. Biết SA = a, AB = a. Tìm góc giữa mặt phẳng ( SBC ) và ( ABC ) .
Lời giải :
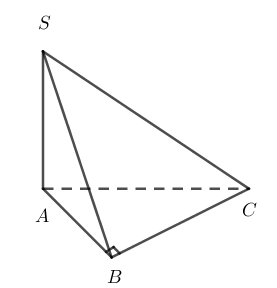
Ta có :
A là hình chiếu của S lên dưới mặt đáy .
BC là giao tuyến của ( SBC ) và ( ABC ) .
B là hình chiếu của A lên BC .
Do đó góc cần tìm là ∠ SBA .
Dễ thấy tam giác SBA vuông cân tại A nên ∠ SBA = 45 º .
3. TÍNH GÓC GIỮA HAI MẶT PHẲNG BẰNG GÓC TAM DIỆN
Góc tam diện là gì?
Giả sử ta có 3 tia chung gốc Ax, Ay, Az. Hình tạo bởi ba góc ∠ xAy, ∠ yAz, ∠ xAz được gọi là góc tam diện. Ta tạm ký hiệu góc tam diện này là ( Ax, Ay, Az ) = ( β, γ, α ) ( hình vẽ ) .
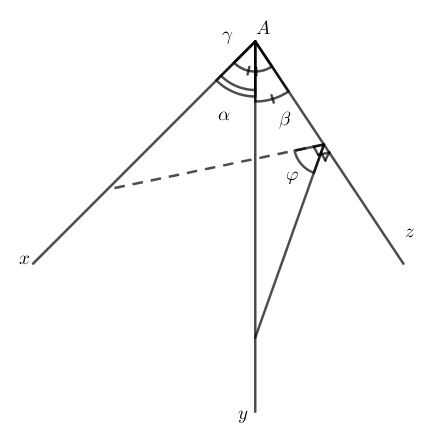
Đồng thời góc phẳng nhị diện tạo bởi hai nửa mặt phẳng chung bờ Az chứa Ax và Ay được gọi là góc phẳng nhị diện đối lập với góc tam diện ∠ xAy. Như hình vẽ trên thì góc nhị diện φ đối lập với góc tam diện α. Các góc khác trọn vẹn tương tự như .
Giả sử ta có góc tam diện α, β, γ và φ là góc nhị diện đối diện với góc α. Khi đó ta có định lý Côsin đối với góc tam diện:
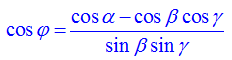
Ứng dụng góc tam diện vào tìm góc giữa hai mặt phẳng
Ta hoàn toàn có thể chia thành những bước như sau cho dễ triển khai
- Xác định thêm mặt phẳng thứ 3 để tạo thành góc tam diện. Mặt phẳng được chọn sao cho góc tam diện phải dễ tính nhất có thể.
- Sử dụng định lý Côsin trong góc tam diện để tính.
Ví dụ:
Cho hình chóp tứ giác đều S.ABCD có toàn bộ những cạnh bằng a. Tính góc giữa mặt bên và dưới mặt đáy .
Lời giải :
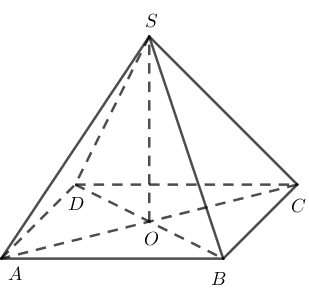
Xét góc tam diện ( BA, BC, BS ) = ( 60 º, 60 º, 90 º ) .
Gọi φ là góc giữa mặt bên ( SBC ) và ( ABCD ) ta có :
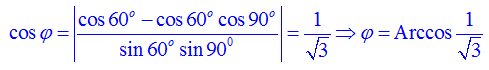
Các bạn để ý có dấu trị tuyệt đối nhé. Đó là vì góc giữa hai mặt phẳng bằng hoặc bù với góc nhị diện.
Chúng ta cũng hoàn toàn có thể kết hợp cách dùng góc nhị diện với góc tam diện để tối ưu cách giải trải qua định lý Sin trong góc tam diện như sau :
Định lý Sin cho góc tam diện
Cho góc tam diện ( α, β, γ ). Các góc nhị diện đối lập với α, β, γ là A, B, C. Khi đó ta có :
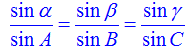
Ví dụ:
Cho hình chóp S.ABC có SA vuông góc với đáy. Đáy là tam giác điều cạnh a. Cạnh bên SA = 3 a / 2. Tính góc giữa ( SAB ) và ( SBC ) .
Lời giải :
Phân tích : Đây là bài toán tính góc giữa mặt bên và mặt đứng. Ta hoàn toàn có thể dựng được góc nhị diện giữa hai mặt đó. Nhưng không phải cũng dễ dạng với ai. Vì vậy ta sử dụng góc tam diện .
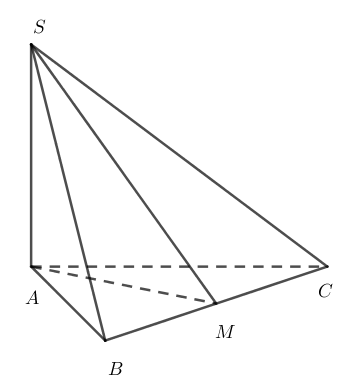
Đầu tiên ta tính góc giữa mặt bên và mặt đáy trước. Dễ thấy góc giữa mặt bên và mặt đáy là ∠SMA với M là trung điểm BC. Các bạn xem lại phần 2 bên trên nhé!
Mặt khác :
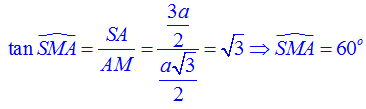
Đây cũng là góc nhị diện của ( BCS ) và ( BCA ) .
Tiếp theo xét góc tam diện ( BA, BS, BC ). Gọi φ là góc nhị diện đối lập với góc ∠ ABC ta có :
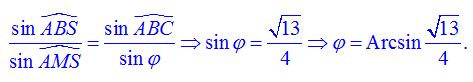
Như vậy, để tính góc giữa mặt bên và mặt đứng ta tính góc giữa mặt bên và mặt dưới ( tất yếu là nếu dễ tính ). Sau đó vận dụng góc tam diện để tính góc giữa mặt bên và mặt đứng. Tất nhiên nếu hoàn toàn có thể vận dụng trực tiếp định lý cos trong góc tam diện thì dùng luôn .
Mỗi giải pháp tính góc 2 mặt phẳng đều có ưu điểm điểm yếu kém. Cách thứ nhất tuy đơn thuần dễ hiểu nhưng trong trường hợp khó dựng góc nhị diện sẽ khó hữu dụng. Còn cách thứ hai tuy nhìn có vẻ như phức tạp hơn. Nhưng nếu chọn được góc tam diện dễ tính thì nó lại rất nhanh, tương thích với làm toán trắc nghiệm. Các bạn nên rèn luyện cả hai cách cho thuần thục. Chúc những bạn học tập vui tươi .
Vectơ – Quan hệ vuông góc –
Source: https://futurelink.edu.vn
Category: Tin tổng hợp