Lý thuyết Hệ thức Vi-ét và ứng dụng.>

Bởi

1. Các kiến thức cần nhớ

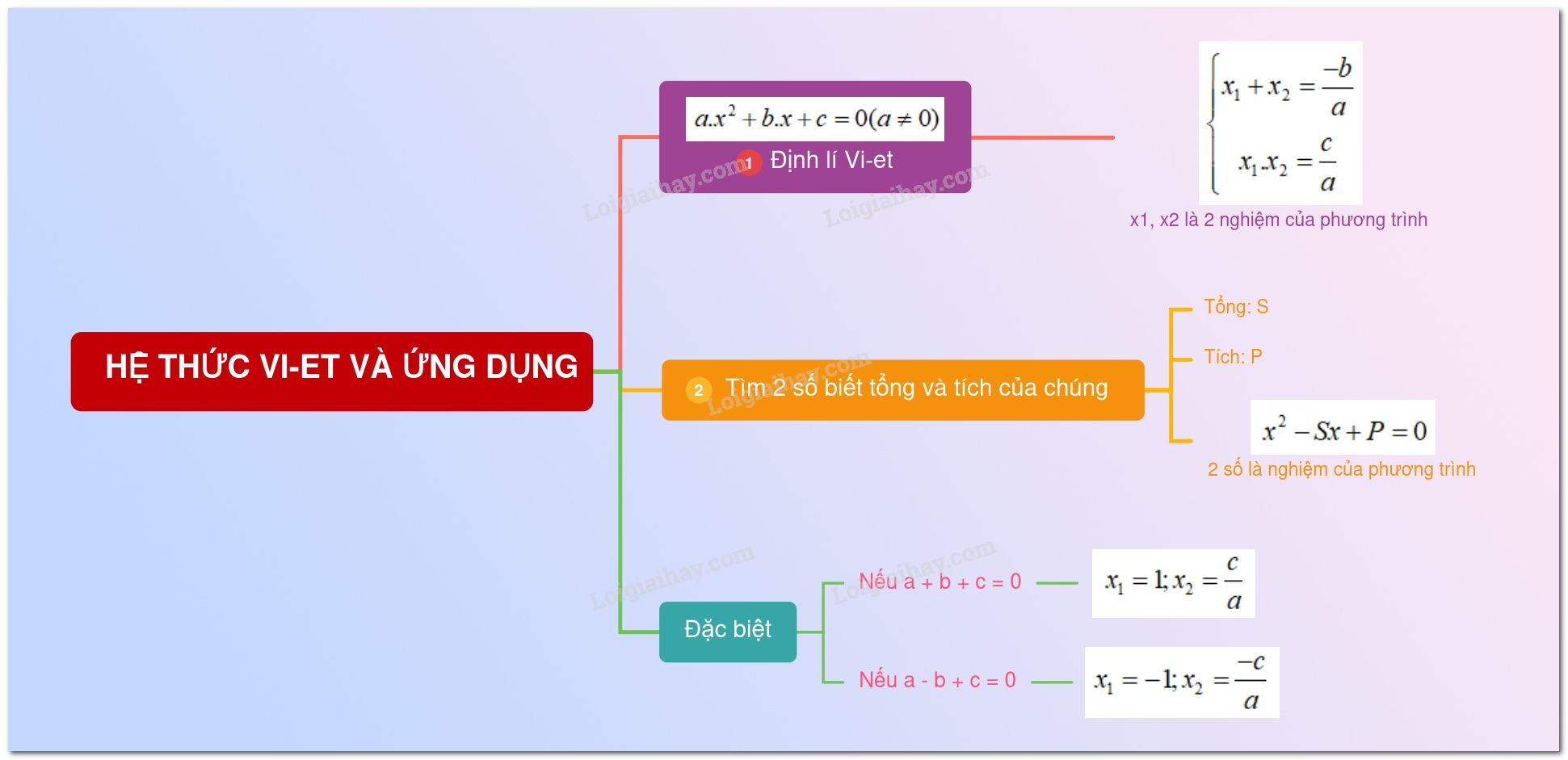
Hệ thức Vi-ét

Cho phương trình bậc hai $a{x^2} + bx + c = 0\,(a \ne 0).$
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ – b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..\)

Ví dụ: Phương trình \(2x^2-5x+2=0\) có \( \Delta=9>0\) nên phương trình có hai nghiệm \(x_1;x_2\).

Theo hệ thức Vi-ét ta có : \ ( \ left \ { \ begin { array } { l } { x_1 } + { x_2 } = \ dfrac { { 5 } } { 2 } \ \ { x_1 } \ cdot { x_2 } = \ dfrac { 2 } { 2 } = 1 \ end { array } \ right .. \ )

Ứng dụng của hệ thức Vi-ét

+ ) Xét phương trình bậc hai : USD a { x ^ 2 } + bx + c = 0 \, ( a \ ne 0 ). $
Nếu phương trình có \ ( a + b + c = 0 \ ) thì phương trình có một nghiệm là \ ( { x_1 } = 1, \ ) nghiệm kia là \ ( { x_2 } = \ dfrac { c } { a }. \ )
Nếu phương trình có \ ( a – b + c = 0 \ ) thì phương trình có một nghiệm là \ ( { x_1 } = – 1, \ ) nghiệm kia là \ ( { x_2 } = – \ dfrac { c } { a }. \ )
+ ) Tìm hai số biết tổng và tích của chúng : Nếu hai số có tổng bằng $ S $ và tích bằng $ P $ thì hai số đó là hai nghiệm của phương trình USD { X ^ 2 } – SX + P = 0 USD ( ĐK : USD { S ^ 2 } \ ge 4P $ )

Ví dụ: 

+ Phương trình \ ( 2 x ^ 2-9 x + 7 = 0 \ ) có \ ( a + b + c = 2 + ( – 9 ) + 7 = 0 \ ) nên có hai nghiệm \ ( x_1 = 1 ; x_2 = \ dfrac { c } { a } = \ dfrac { 7 } { 2 } \ )
+ Phương trình \ ( 2 x ^ 2 + 9 x + 7 = 0 \ ) có \ ( a-b+c = 2-9 + 7 = 0 \ ) nên có hai nghiệm \ ( x_1 = – 1 ; x_2 = – \ dfrac { c } { a } = – \ dfrac { 7 } { 2 } \ )

2. Các dạng toán thường gặp

Dạng 1: Không giải phương trình, tính giá trị biểu thức liên quan giữa các nghiệm.

Phương pháp:

Bước 1 : Tìm điều kiện để phương trình có nghiệm : $\left\{ \begin{array}{l}a \ne 0\\\Delta  \ge 0\end{array} \right.$. Từ đó áp dụng hệ thức Vi-ét ta có : $S = {x_1} + {x_2} =  – \dfrac{b}{a}$ và $P = {x_1}{x_2} = \dfrac{c}{a}$.

Bước 2 : Biến đổi biểu thức đối xứng giữa các nghiệm của đề bài theo tổng ${x_1} + {x_2}$ và tích ${x_1}{x_2}$, sau đó áp dụng bước 1.

Một số biểu thức đối xứng giữa các nghiệm thường gặp là :

+ ) $ A = x_1 ^ 2 + x_2 ^ 2 = { \ left ( { { x_1 } + { x_2 } } \ right ) ^ 2 } – 2 { x_1 } { x_2 } = { S ^ 2 } – 2P $
+ ) $ B = x_1 ^ 3 + x_2 ^ 3 USD
USD = { \ left ( { { x_1 } + { x_2 } } \ right ) ^ 3 } – 3 { x_1 } { x_2 } \ left ( { { x_1 } + { x_2 } } \ right ) = { S ^ 3 } – 3SP $
+ ) $ C = x_1 ^ 4 + x_2 ^ 4 = { \ left ( { x_1 ^ 2 + x_2 ^ 2 } \ right ) ^ 2 } – 2 x_1 ^ 2 x_2 ^ 2 USD
USD = { \ left [ { { { \ left ( { { x_1 } + { x_2 } } \ right ) } ^ 2 } – 2 { x_1 } { x_2 } } \ right ] ^ 2 } – 2 { \ left ( { { x_1 } { x_2 } } \ right ) ^ 2 } = { \ left ( { { S ^ 2 } – 2P } \ right ) ^ 2 } – 2 { P ^ 2 } $
+ ) USD D = \ left | { { x_1 } – { x_2 } } \ right | $
USD = \ sqrt { { { \ left ( { { x_1 } + { x_2 } } \ right ) } ^ 2 } – 4 { x_1 } { x_2 } } $ .
+ )
USD E = { \ left ( { { x_1 } – { x_2 } } \ right ) ^ 2 } = { \ left ( { { x_1 } + { x_2 } } \ right ) ^ 2 } – 4 { x_1 } { x_2 } $
USD = { S ^ 2 } – 4P $ .

Dạng 2 : Giải phương trình bằng cách nhẩm nghiệm

Phương pháp :

Xét phương trình bậc hai : USD a { x ^ 2 } + bx + c = 0 { \ rm { } } \ left ( { a \ ne 0 } \ right ) USD .+ ) Nếu phương trình có USD a + b + c = 0 $ thì phương trình có một nghiệm $ { x_1 } = 1 USD, nghiệm kia là $ { x_2 } = \ dfrac { c } { a }. $+ ) Nếu phương trình có $ a – b + c = 0 $ thì phương trình có một nghiệm $ { x_1 } = – 1 USD, nghiệm kia là $ { x_2 } = – \ dfrac { c } { a }. $+ ) Nếu $ { x_1 }, { x_2 } $ là hai nghiệm của phương trình thì $ \ left \ { \ begin { array } { l } S = { x_1 } + { x_2 } = – \ dfrac { b } { a } \ \ P = { x_1 } { x_2 } = \ dfrac { c } { a } \ end { array } \ right. $ .

Dạng 3 : Phân tích tam thức bậc hai thành nhân tử

Phương pháp :

Nếu tam thức bậc hai USD a { x ^ 2 } + bx + c { \ rm { } } \ left ( { a \ ne 0 } \ right ) USD có hai nghiệm $ { x_1 } $ và $ { x_2 } $ thì nó được nghiên cứu và phân tích thành nhân tử : USD a { x ^ 2 } + bx + c = a \ left ( { x – { x_1 } } \ right ) \ left ( { x – { x_2 } } \ right ) USD .

Dạng 4 : Tìm hai số khi biết tổng và tích

Phương pháp :

Để tìm hai số USD x, y $ khi biết tổng $ S = x + y $ và tích $ P = xy USD, ta làm như sau :Bước 1 : Xét điều kiện kèm theo USD { S ^ 2 } \ ge 4P USD. Giải phương trình USD { X ^ 2 } – SX + P = 0 $ để tìm những nghiệm $ { X_1 }, { X_2 } $ .Bước 2 : Khi đó những số cần tìm USD x, y $ là USD x = { X_1 }, y = { X_2 } $ hoặc USD x = { X_2 }, y = { X_1 } $ .

Dạng 5 : Bài toán liên quan đến dấu các nghiệm của phương trình bậc hai

Phương pháp :

Xét phương trình \ ( a { x ^ 2 } + bx + c = 0 \ left ( { a \ ne 0 } \ right ) \ ). Khi đó :1. Phương trình có hai nghiệm trái dấu \ ( \ Leftrightarrow ac < 0 \ ) .2. Phương trình có hai nghiệm phân biệt cùng dấu \ ( \ Leftrightarrow \ left \ { \ begin { array } { l } \ Delta > 0 \ \ P > 0 \ end { array } \ right. \ ) .3. Phương trình có hai nghiệm dương phân biệt \ ( \ Leftrightarrow \ left \ { \ begin { array } { l } \ Delta > 0 \ \ P > 0 \ \ S > 0 \ end { array } \ right. \ ) .4. Phương trình có hai nghiệm âm phân biệt \ ( \ Leftrightarrow \ left \ { \ begin { array } { l } \ Delta > 0 \ \ P > 0 \ \ S < 0 \ end { array } \ right. \ ) .5. Phương trình có hai nghiệm trái dấu mà nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương \ ( \ Leftrightarrow \ left \ { \ begin { array } { l } ac < 0 \ \ S < 0 \ end { array } \ right. \ ) .

Dạng 6 : Xác  định điều kiện của tham số để nghiệm của phương trình thỏa mãn điều kiện cho trước.

Phương pháp :

Bước 1. Tìm điều kiện để phương trình có nghiệm \(\left\{ \begin{array}{l}a \ne 0\\\Delta  \ge 0\end{array} \right.\).

Bước 2. Từ hệ thức đã cho và hệ thức Vi-ét, tìm được điều kiện của tham số.

Bước 3. Kiểm tra điều kiện của tham số xem có thỏa mãn điều kiện ở bước 1 hay không rồi kết luận.