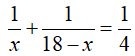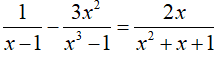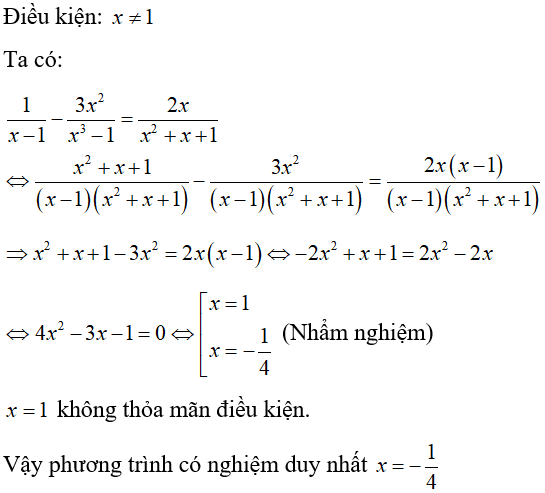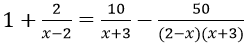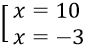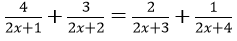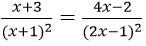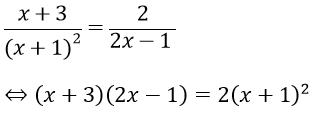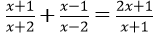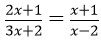Cách giải phương trình chứa ẩn ở mẫu nhanh nhất và bài tập ứng dụng
Minh Vũ
8 giờ trước
Giải phương trình chứa ẩn ở mẫu một cách nhanh gọn, đúng mực không phải học viên nào cũng thuận tiện chớp lấy. Mặc dù đây là phần kiến thức và kỹ năng Đại số 8 vô cùng quan trọng. Bài viết thời điểm ngày hôm nay, Zicxabooks. com sẽ trình làng cùng những bạn cách giải phương trình chứa ẩn ở mẫu nhanh nhất và nhiều bài tập ứng dụng khác. Bạn khám phá nhé !
I. LÝ THUYẾT CẦN GHI NHỚ
1. Phương trình chứa ẩn ở mẫu là gì ?
Phương trình chứa ẩn ở mẫu là phương trình có biểu thức chứa ẩn ở mẫu .
Ví dụ :
2 / y + 3 = 0 là phương trình chứa ẩn ở mẫu ( ẩn y )
2-4 / x2 + 2 x + 7 = 0 là phương trình chứa ẩn ở mẫu ( ẩn x )
Ta thấy, việc tìm điều kiện kèm theo xác lập là rất quan trọng trong việc tìm nghiệm của một phương trình. Sau đây, chúng tôi sẽ hướng dẫn giải pháp tìm điều kiện kèm theo xác lập của một phương trình .
2. Tìm điều kiện xác định của một phương trình
Điều kiện xác lập của phương trình là tập hợp những giá trị của ẩn làm cho tổng thể những mẫu trong phương trình đều khác 0 .
Điều kiện xác lập của phương trình viết tắt là ĐKXĐ .
Ví dụ: Tìm điều kiện xác định của các phương trình sau
a ) ( x – 1 ) / ( x + 2 ) + 1 = 1 / ( x – 2 ) .
b ) ( x – 1 ) / ( 1 – 2 x ) = 1 .
Hướng dẫn:
a ) Ta thấy x + 2 ≠ 0 khi x ≠ – 2 và x – 2 ≠ 0 khi x ≠ 2 .
Do đó ĐKXĐ của phương trình ( x – 1 ) / ( x + 2 ) + 1 = 1 / ( x – 2 ) là x ≠ ± 2 .
b ) Ta thấy 1 – 2 x ≠ 0 khi x ≠ 1/2 .
Do đó ĐKXĐ của phương trình ( x – 1 ) / ( 1 – 2 x ) = 1 là x ≠ 1/2 .
II. CÁCH GIẢI PHƯƠNG TRÌNH CHỨA ẨN Ở MẪU
A. Phương pháp:
Bước 1 : Tìm điều kiện kèm theo xác lập .
Bước 2 : Quy đồng, khử mẫu, rút gọn đưa về dạng phương trình bậc hai .
Bước 3 : Giải phương trình bậc hai .
Bước 4 : So sánh với điều kiện kèm theo và Kết luận .
B. Các ví dụ điển hình
Ví dụ 1: Giải phương trình
Lời giải
Chọn A
Ví dụ 2: Cho phương trình 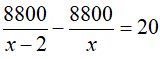
Lời giải
Chọn D
Ví dụ 3: Giải phương trình
Lời giải
Chọn
III. BÀI TẬP CÁCH GIẢI PHƯƠNG TRÌNH CHỨA ẨN Ở MẪU
Bài 1:
Giải phương trình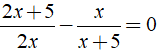
Hướng dẫn:
+ ĐKXĐ : x ≠ 0 ; x ≠ – 5 .
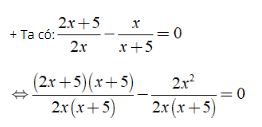
⇒ ( 2 x + 5 ) ( x + 5 ) – 2×2 = 0
⇔ 2×2 + 10 x + 5 x + 25 – 2×2 = 0 ⇔ 15 x = – 25 ⇔ x = – 5/3 .
+ So sánh với ĐKXĐ ta thấy x = – 5/3 thỏa mãn nhu cầu điều kiện kèm theo .
Vậy phương trình đã cho có tập nghiệm là S = { – 5/3 } .
Bài 2: Giải phương trình
Hướng dẫn:
ĐKXĐ : x ≠ – 3 và x ≠ 2
Phương trình tương tự với ( 2 – x ) ( x + 3 ) – 2 ( x + 3 ) = 10 ( 2 – x ) – 50
⇔ x2 – 7x – 30 = 0 ⇔
Đối chiếu với điều kiện kèm theo ta có nghiệm của phương trình là x = 10
Bài 3: Giải các phương trình sau:
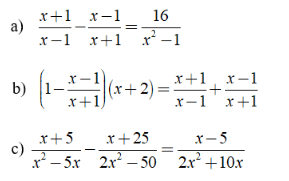
Hướng dẫn:
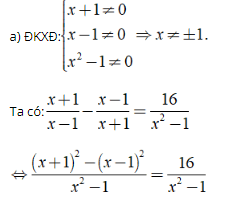
⇔ ( x + 1 ) 2 – ( x – 1 ) 2 = 16
⇔ (x2 + 2x + 1) – (x2 – 2x + 1) = 16
⇔ 4 x = 16 ⇔ x = 4 .
Vây phương trình đã cho có nghiệm x = 4 .
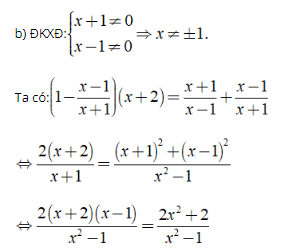
⇔ 2 ( x2 + x – 2 ) = 2×2 + 2
⇔ 2 x = 6 ⇔ x = 3 .
Vậy phương trình đã cho có nghiệm là x = 3 .
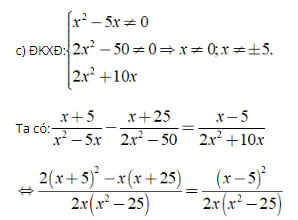
⇔ 2 ( x2 + 10 x + 25 ) – ( x2 + 25 x ) = x2 – 10 x + 25
⇔ x2 – 5 x + 50 = x2 – 10 x + 25
⇔ 5 x = – 25 ⇔ x = – 5 .
Vậy phương trình đã cho có nghiệm x = – 5 .
Bài 4: Giải các phương trình sau:
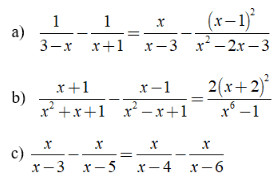
Hướng dẫn:
a ) ĐKXĐ : x ≠ – 1 ; x ≠ 3 .
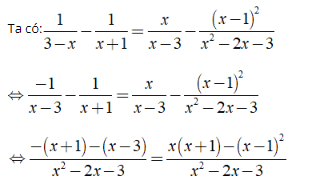
⇔ – x – 1 – x + 3 = x2 + x – x2 + 2 x – 1
⇔ 5 x = 3 ⇔ x = 3/5 .
Vậy phương trình đã cho có nghiệm là x = 3/5 .
b ) ĐKXĐ : x ≠ 3, x ≠ 4, x ≠ 5, x ≠ 6 .
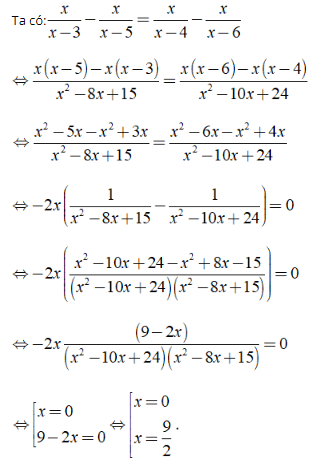
Vậy phương trình đã cho có nghiệm là x = 0 ; x = 9/2 .
c ) ĐKXĐ : x ≠ 1 .
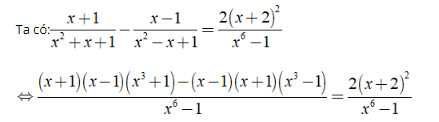
⇔ ( x2 – 1 ) ( x3 + 1 ) – ( x2 – 1 ) ( x3 – 1 ) = 2 ( x2 + 4 x + 4 )
⇔ ( x5 + x2 – x3 – 1 ) – ( x5 – x2 – x3 + 1 ) = 2 ( x2 + 4 x + 4 )
⇔ 2×2 – 2 = 2×2 + 8 x + 8
⇔ 8 x = – 10 ⇔ x = – 5/4 .
Vậy phương trình đã cho có nghiệm là x = – 5/4 .
Bài 5: Giải phương trình
Hướng dẫn:
ĐKXĐ : x ∉ { – 2 ; – 3/2 ; – 1 ; – 1/2 }
Phương trình tương tự với
Vậy phương trình có nghiệm là x = ( – 5 ± √ 3 ) / 4 và x = – 5/2
Bài 6: Giải phương trình
Hướng dẫn:
ĐKXĐ : x ≠ – 1 và x ≠ 1/2
Phương trình tương tự với
⇔ x = 5 ( thỏa mãn nhu cầu điều kiện kèm theo )
Vậy phương trình có nghiệm là x = 5
Bài 7: Giải phương trình
Hướng dẫn:
ĐKXĐ : x ≠ ± 2 và x ≠ – 1
Phương trình tương tự với
( x + 1 ) 2 ( x-2 ) + ( x-1 ) ( x + 1 ) ( x + 2 ) = ( 2 x + 1 ) ( x-2 ) ( x + 2 )
⇔ ( x2 + 2 x + 1 ) ( x – 2 ) + ( x2 – 1 ) ( x + 2 ) = ( 2 x + 1 ) ( x2 – 4 )
⇔ x3 – 2×2 + 2×2 – 4 x + x – 2 + x3 + 2×2 – x – 2 = 2×3 – 8 x + x2 – 4
⇔ x2 + 4x = 0 ⇔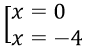
Vậy phương trình có nghiệm là x = – 4 và x = 0
Bài 8: Giải phương trình
Hướng dẫn:
ĐKXĐ : x ≠ – 2/3 và x ≠ 2
Phương trình tương tự với ( 2 x + 1 ) ( x-2 ) = ( x + 1 ) ( 3 x + 2 )
⇔ 2×2 – 4 x + x – 2 = 3×2 + 2 x + 3 x + 2
⇔ x2 + 8 x + 4 = 0 ⇔ x = – 4 ± 2 √ 3 ( thỏa mãn nhu cầu điều kiện kèm theo )
Vậy phương trình có nghiệm là x = -4 ± 2√3
Trên đây, Zicxabooks.com.vn đã giới thiệu đến quý thầy cố và các bạn học sinh chuyên đề phương trình chứa ẩn ở mẫu và cách giải phương trình chứa ẩn ở mẫu nhanh nhất cùng nhiều bài tập vận dụng khác. Hi vọng, bài viết đã mang đến cho bạn những thông tin hữu ích. Xem thêm cách giải phương trình bậc nhất một ẩn tại đường link này bạn nhé !
Từ khóa ngẫu nhiên
Source: https://futurelink.edu.vn
Category: Tin tổng hợp