Trong bài viết này, chúng tôi sẽ chia sẻ lý thuyết về phương trình đường thẳng và các dạng phương trình tham số, phương trình tổng quát, phương trình chính tắc,..và các dạng bài tập thường gặp nhất ở các đề thi đại học hiện nay để các bạn cùng tham khảo nhé
Phương trình đường thẳng trong mặt phẳng
1. Phương trình tổng quát
Phương trình Δ : ax + by + c = 0, a2 + b2 ≠ 0 là PTTQ của đường thẳng Δ nhận n → ( a ; b ) làm vectơ pháp tuyến của đường thẳng
Các dạng đặc biệt của phương trình đường thẳng.
- Δ: ax + c = 0,(a≠0) nên Δ song song hoặc trùng với Oy.
- Δ: by + c = 0,(a≠0) nên Δ song song hoặc trùng với Ox.
- Δ: ax + by = 0, a2 + b2 ≠ 0 nên Δ đi qua gốc tọa độ.
2. Phương trình đường thẳng theo đoạn chắn
Đường thẳng cắt Ox và Oy lần lượt tại 2 điểm A(a; 0) và B(0; b) có phương trình đoạn theo chắn là x/a + y/b = 1 (a, b ≠ 0)
3. Phương trình tham số
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua điểm M ( x0, y0 ) và nhận u → = ( u1, u2 ) làm vectơ chỉ phương. Khi đó phương trình tham số của d là
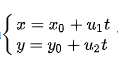
với t được gọi là tham số. Với mỗi giá trị t ∈ R ta được một điểm thuộc đường thẳng .
4. Phương trình chính tắc
Phương trình chính tắc của đường thẳng Δ đi qua M0 ( x0, y0 ) và có vecto chỉ phương u → = ( u1, u2 ) là
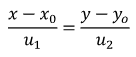
Với u1, u2 ≠ 0
5. Hệ số góc của đường thẳng
Cho đường thẳng d cắt trục Ox tại M và tia Mt là một phần của đường thẳng nằm ở nửa mặt phẳng có bờ là trục Ox mà những điểm trên nửa mặt phẳng đó có tung độ dương, khi đó tia Mt hợp với tia Mx một góc α. Đặt k = tanα, khi đó k được gọi là thông số góc của đường thẳng d .
Đường thẳng có vecto chỉ phương u → = ( u1, u2 ) thì có thông số góc k = u1 / u2
Đường thẳng có vectơ pháp tuyến n → = ( a, b ) thì có thông số góc k = – a / b
Hai đường thẳng song song có thông số góc bằng nhau .
Hai đường thẳng vuông góc có tích 2 thông số góc là – 1 .
6. Vị trí tương đối giữa 2 đường thẳng
Xét 2 đường thẳng D1 : a1x + b1y + c1 = 0 ; D2 : a2x + b2y + c2 = 0. Tọa độ giao điểm D1, D2 là nghiệm của hệ phương trình :
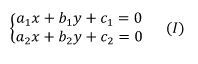
Ta có những trường hợp sau :
- Hệ (I) có một nghiệm (x0; y0), khi D1 cắt D2 tại M0(x0; y0)
- Hệ (I) có vô số nghiệm khi D1 trùng D2
- Hệ (I) vô nghiệm khi D1 // D2
Lưu ý: Nếu a2, b2, c2 ≠ 0 thì
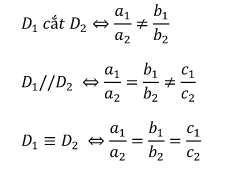 →
→
7 Góc giữa 2 đường thẳng
Cho đường thẳng Δ1 : a1x + b1y + c1 = 0 có vecto pháp tuyến n → 1 và Δ2 : a2x + b2y + c2 = 0 có vecto pháp tuyến n → 2
Đặt j = ( Δ1, Δ2 ), khi đó
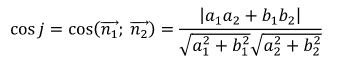
Lưu ý:
- Δ1⊥ Δ2 ⇔ n→1⊥ n→2 ⇔ a1a2 + b1b2 = 0
- Nếu Δ1 và Δ2 có phương trình đường thẳng là y = k1x + m1 và y = k2x + m2 thì Δ1⊥ Δ2 ⇔ k1k2 = -1
8. Khoảng cách từ một điểm đến đường thẳng
Cho đường thẳng ( d ) ax + by + c = 0 và M ( x0 ; y0 ) ∉ ( d ), khoảng cách từ điểm M đến ( d ) được tính theo công thức
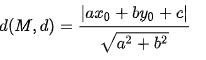
Tham khảo thêm :
Phương trình đường thẳng trong không gian
1. Dạng tham số
Trong khoảng trống với hệ trục tọa độ Oxyz, cho đường thẳng d đi qua điểm M ( x0, y0, z0 và nhận u → = ( u1, u2, u3 ) làm vectơ chỉ phương. Khi đó phương trình tham số của d là
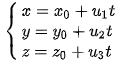
với t được gọi là tham số. Với mỗi giá trị t ∈ R ta được một điểm thuộc đường thẳng .
2. Dạng chính tắc
Nếu cả u1, u2, u3 đều khác 0, từ phương trình tham số ta khử tham số t, ta được phương trình chính tắc
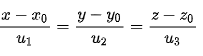
3. Vị trí tương đối giữa 2 đường thẳng

Các dạng bài tập phương trình đường thẳng
Dạng 1: Viết phương trình tham số của đường thẳng.
Để viết phương trình tham số của đường thẳng ∆ ta triển khai những bước như sau :

Ví dụ : Đường thẳng đi qua hai điểm A ( 3 ; – 7 ) và B ( 1 ; – 7 ) có phương trình tham số là :

Dạng 2:Viết phương trình tổng quát của đường thẳng
Để viết phương trình tổng quát của đường thẳng ∆ ta thực thi những bước như sau :
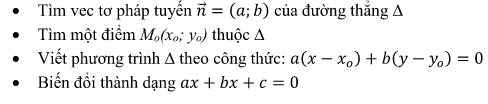
Lưu ý:
Nếu đường thẳng ∆1 cùng phương với đường thẳng ∆2: ax + by + c = 0 thì ∆1 có phương trình tổng quát là: ax + by + c’ = 0
Nếu đường thẳng ∆1 vuông góc có với đường thẳng ∆2: ax + by + c = 0 thì ∆1 có phương trình tổng quát là: –bx + ay + c’ = 0
Ví dụ : Đường thẳng đi qua A ( 1 ; – 2 ), nhận n → = ( 1 ; – 2 ) làm véc tơ pháp tuyến có phương trình là :
A. x – 2 y + 1 = 0 ; B. 2 x + y = 0 ; C. x – 2 y – 5 = 0 ; D. x – 2 y + 5 = 0
Lời giải
Gọi ( d ) là đường thẳng đi qua A và nhận n → = ( 1 ; – 2 ) làm VTPT
=> Phương trình đường thẳng ( d ) : 1 ( x – 1 ) – 2 ( y + 2 ) = 0 hay x – 2 y – 5 = 0
Dạng 3: Vị trí tương đối của hai đường thẳng
Để xét vị trí tương đối của hai đường thẳng ∆ 1 : a1x + b1y + c1 = 0 ; ∆ 2 : a2x + b2y + c2 = 0, ta xét những trường hợp sau :

Dạng 4: Khoảng cách từ một điểm đến một đường thẳng
Để tính khoảng cách từ điểm Mo ( xo ; yo ) đến đường thẳng ∆ : ax + by + c = 0, ta dùng công thức :
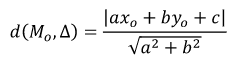
Sau khi đọc xong bài viết của chúng tôi những bạn hoàn toàn có thể mạng lưới hệ thống lại kỹ năng và kiến thức về phương trình đường thẳng và những dạng bài tập thường gặp để vận dụng giải bài tập nhanh gọn và đúng mực nhé
Đánh giá bài viết
Source: https://futurelink.edu.vn
Category: Tin tổng hợp