Giải bài 1, 2, 3 trang 7 SGK Toán 9 tập 2

Bởi

Bài 1 trang 7 sgk toán 9 tập 2

1. Trong những cặp số \ ( ( – 2 ; 1 ) \ ), \ ( ( 0 ; 2 ) \ ), \ ( ( – 1 ; 0 ) \ ), \ ( ( 1,5 ; 3 ) \ ) và \ ( ( 4 ; – 3 ) \ ), cặp số nào là nghiệm của phương trình :
a ) \ ( 5 x + 4 y = 8 \ ) ? b ) \ ( 3 x + 5 y = – 3 \ ) ?

Giải:

a ) Thay từng cặp số đã cho vào phương trình \ ( 5 x + 4 y = 8 \ ), ta được :
+ ) \ ( 5 ( – 2 ) + 4. 1 = – 10 + 4 = – 6 ≠ 8 \ ) nên cặp số \ ( ( – 2 ; 1 ) \ ) không là nghiệm của phương trình .
+ ) \ ( 5. 0 + 4. 2 = 8 \ ) nên cặp số \ ( ( 0 ; 2 ) \ ) là nghiệm của phương trình .
+ ) \ ( 5. ( – 1 ) + 4. 0 = – 5 ≠ 8 \ ) nên \ ( ( – 1 ; 0 ) \ ) không là nghiệm của phương trình .
+ ) \ ( 5. 1,5 + 4. 3 = 7,5 + 12 = 19,5 ≠ 8 \ ) nên \ ( ( 1,5 ; 3 ) \ ) không là nghiệm của phương trình .
+ ) \ ( 5. 4 + 4. ( – 3 ) = 20 – 12 = 8 \ ) nên \ ( ( 4 ; – 3 ) \ ) là nghiệm của phương trình .
Vậy có hai cặp số \ ( ( 0 ; 2 ) \ ) và \ ( ( 4 ; – 3 ) \ ) là nghiệm của phương trình \ ( 5 x + 4 y = 8 \ ) .
b ) Thay từng cặp số đã cho vào phương trình \ ( 3 x + 5 y = – 3 \ ) ta được :
+ ) \ ( 3. ( – 2 ) + 5. 1 = – 6 + 5 = – 1 ≠ – 3 \ ) nên \ ( ( – 2 ; 1 ) \ ) không là nghiệm của phương trình .
+ ) \ ( 3. 0 + 5. 2 = 10 ≠ – 3 \ ) nên \ ( ( 0 ; 2 ) \ ) không là nghiệm của phương trình .
+ ) \ ( 3. ( – 1 ) + 5. 0 = – 3 \ ) nên ( – 1 ; 0 ) là nghiệm của phương trình .
+ ) \ ( 3. 1,5 + 5. 3 = 4,5 + 15 = 19,5 ≠ – 3 \ ) nên \ ( ( 1,5 ; 3 ) \ ) không là nghiệm của phương trình .
+ ) \ ( 3. 4 + 5. ( – 3 ) = 12 – 15 = – 3 \ ) nên \ ( ( 4 ; – 3 ) \ ) là nghiệm của phương trình .
Vậy có hai cặp số \ ( ( – 1 ; 0 ) \ ) và \ ( ( 4 ; – 3 ) \ ) là nghiệm của phương trình \ ( 3 x + 5 y = – 3 \ ) .

Bài 2 trang 7 sgk Toán 9 tập 2

2. Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó :
a ) \ ( 3 x – y = 2 \ ) ; b ) \ ( x + 5 y = 3 \ ) ;
c ) \ ( 4 x – 3 y = – 1 \ ) ; d ) \ ( x + 5 y = 0 \ ) ;
e ) \ ( 4 x + 0 y = – 2 \ ) ; f ) \ ( 0 x + 2 y = 5 \ ) .

Bài giải:

a ) Ta có phương trình \ ( 3 x – y = 2 \ ) ( 1 )
( 1 ) ⇔ \ ( \ left \ { \ begin { matrix } x \ in R và và \ \ y = 3 x – 2 và và \ end { matrix } \ right. \ )
Ta được nghiệm tổng quát của phương trình là : \ ( ( x ; 3 x – 2 ) \ )
* Vẽ đưởng thẳng biểu diễn tập nghiệm của phương trình \ ( y = 3 x – 2 \ ) :
Cho \ ( x = 0 \ Rightarrow y = – 2 \ ) ta được \ ( A ( 0 ; – 2 ) \ ) .
Cho \ ( y = 0 \ Rightarrow x = { 2 \ over 3 } \ ) ta được \ ( B ( \ frac { 2 } { 3 } ; 0 ) \ ) .
Biểu diễn cặp số \ ( A ( 0 ; – 2 ) \ ) và \ ( B ( \ frac { 2 } { 3 } ; 0 ) \ ) trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình \ ( 3 x – y = 2 \ ) .

b ) Ta có phương trình \ ( x + 5 y = 3 \ ) ( 2 )
( 2 ) ⇔ \ ( \ left \ { \ begin { matrix } x = – 5 y + 3 và và \ \ y \ in R và và \ end { matrix } \ right. \ )
Ta được nghiệm tổng quát của phương trình là ( – 5 y + 3 ; y ) .
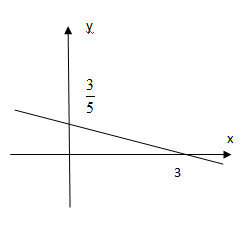
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \ ( x = – 5 y + 3 \ ) :
+ ) Cho \ ( x = 0 \ Rightarrow y = { 3 \ over 5 } \ ) ta được \ ( A \ left ( { 0 ; { 3 \ over 5 } } \ right ) \ ) .
+ ) Cho \ ( y = 0 \ Rightarrow x = 3 \ ) ta được \ ( B \ left ( { 3 ; 0 } \ right ) \ ) .
Biểu diễn cặp số \ ( A \ left ( { 0 ; { 3 \ over 5 } } \ right ) \ ), \ ( B \ left ( { 3 ; 0 } \ right ) \ ) trên hệ trục toa độ và đường thẳng AB chính là tập nghiệm của phương trình .

     

c ) Ta có phương trình \ ( 4 x – 3 y = – 1 \ ) ( 3 )

   (3) ⇔ \(\left\{\begin{matrix} x \in R & & \\ y = \frac{4}{3}x + \frac{1}{3}& & \end{matrix}\right.\)

Ta được nghiệm tổng quát của phương trình là : \ ( \ left ( { x ; { 4 \ over 3 } x + { 1 \ over 3 } } \ right ) \ ) .
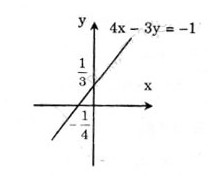
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \ ( 4 x – 3 y = – 1 \ )
+ ) Cho \ ( x = 0 \ Rightarrow y = { 1 \ over 3 } \ ) ta được \ ( A \ left ( { 0 ; { 1 \ over 3 } } \ right ) \ )
+ ) Cho \ ( y = 0 \ Rightarrow x = – { { 1 } \ over 4 } \ ) ta được \ ( B \ left ( { – { 1 \ over 4 } ; 0 } \ right ) \ )
Biểu diễn cặp số \ ( A ( 0 ; \ frac { 1 } { 3 } ) \ ) và \ ( B ( – \ frac { 1 } { 4 } \ ) ; 0 ) trên hệ tọa độ và đường thẳng AB chính là tập nghiệm của phương trình \ ( 4 x – 3 y = – 1 \ ) .

 

d ) Ta có phương trình \ ( x + 5 y = 0 \ ) ( 4 )
( 4 ) ⇔ \ ( \ left \ { \ begin { matrix } x = – 5 y và và \ \ y \ in R và và \ end { matrix } \ right. \ )
Ta được nghiệm tổng quát của phương trình là : \ ( ( – 5 y ; y ) \ ) .
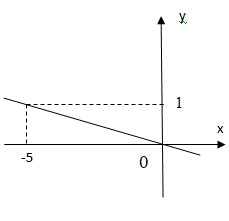
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \ ( x + 5 y = 0 \ )
+ ) Cho \ ( x = 0 \ Rightarrow y = 0 \ ) ta được \ ( O \ left ( { 0 ; 0 } \ right ) \ )
+ ) Cho \ ( y = 1 \ Rightarrow x = – 5 \ ) ta được \ ( A \ left ( { – 5 ; 1 } \ right ) \ ) .
Biểu diễn cặp số \ ( O ( 0 ; 0 ) \ ) và \ ( A ( – 5 ; 1 ) \ ) trên hệ tọa độ và đường thẳng OA chính là tập nghiệm của phương trình \ ( x + 5 y = 0 \ ) .

  

e ) Ta có phương trình \ ( 4 x + 0 y = – 2 \ ) ( 5 )
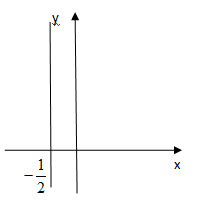
( 5 ) ⇔ \ ( \ left \ { \ begin { matrix } x = – \ frac { 1 } { 2 } và và \ \ y \ in R và và \ end { matrix } \ right. \ )
Ta được nghiệm tổng quát của phương trình là : \ ( \ left ( – { 1 \ over 2 } ; y \ right ) \ )
Tập nghiệm là đường thẳng \ ( x = – \ frac { 1 } { 2 } \ ), qua \ ( A ( – \ frac { 1 } { 2 } ; 0 ) \ ) và song song với trục tung .

  

f ) 0 x + 2 y = 5 ( 6 )
( 6 ) ⇔ \ ( \ left \ { \ begin { matrix } x \ in R và và \ \ y = \ frac { 5 } { 2 } và và \ end { matrix } \ right. \ )
Ta được nghiệm tổng quát của phương trình là \ ( \ left ( { x ; { 5 \ over 2 } } \ right ) \ )
Tập nghiệm là đường thẳng \ ( y = { 5 \ over 2 } \ ) qua \ ( A \ left ( { 0 ; { 5 \ over 2 } } \ right ) \ ) và song song với trục hoành .

  

Bài 3 trang 7 sgk Toán 9 tập 2

3. Cho hai phương trình x + 2 y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của những phương trình nào .

Bài giải:

* Vẽ đường thẳng \ ( x + 2 y = 4 \ ) .
– Cho \ ( x = 0 \ Rightarrow y = 2 \ ) ta được \ ( A ( 0 ; 2 ) \ ) .
– Cho \ ( y = 0 \ Rightarrow x = 4 \ ) ta được \ ( B ( 4 ; 0 ) \ ) .
Đường thẳng cần vẽ là đường thẳng đi qua A, B .

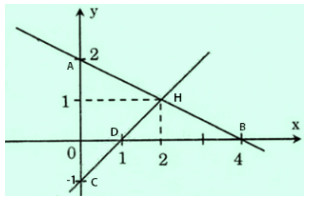
* Vẽ đường thẳng \ ( x – y = 1 \ ) .
– Cho \ ( x = 0 \ Rightarrow y = – 1 \ ) ta được C ( 0 ; – 1 ) .
– Cho \ ( y = 0 \ Rightarrow x = 1 \ ) ta được D ( 1 ; 0 ) .

Đường thẳng cần vẽ là đường thẳng đi qua C, D.

* Giao điểm của hai đường thẳng có tọa độ là ( 2 ; 1 ) .
Ta có ( 2 ; 1 ) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho .

Giaibaitap.me