LÍ THUYẾT
DAO ĐỘNG ĐIỀU HÒA
I – Khái niệm
– Dao động cơ: Là chuyển động qua lại của vật quanh một vị trí cân bằng (thường là vị trí của vật khi đứng yên).
Bạn đang đọc: Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 8 9 sgk Vật Lí 12
Ví dụ : chiếc thuyền nhấp nhô tại chỗ neo, hoạt động đung đưa của chiếc lá, …
– Dao động tuần hoàn : Là giao động cơ mà sau những khoảng chừng thời hạn bằng nhau vật trở lại vị trí cũ theo hướng cũ .
Ví dụ : xê dịch của con lắc đồng hồ đeo tay .
– Dao động điều hòa : Là giao động trong đó li độ ( vị trí ) của vật là một hàm côsin ( hay sin ) của thời hạn. ( là xê dịch tuần hoàn đơn thuần nhất ) .
II – Phương trình dao động điều hòa
Một điểm xê dịch điều hòa trên một đoạn thẳng luôn luôn hoàn toàn có thể được coi là hình chiếu của một điểm tương ứng hoạt động tròn đều lên đường kính là đoạn thẳng đó ( Hình 1.1 )
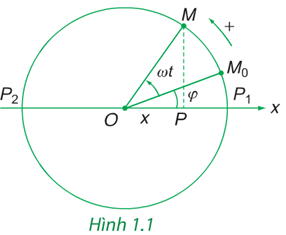
Giả sử tại thời gian t = 0, điểm M ở vị trí M0 được xác lập bằng góc \ ( \ varphi \ )
Tại thời gian t vị trí của M là \ ( \ left ( { \ omega t + \ varphi } \ right ) \ )
Khi đó, hình chiếu P. của M có tọa độ \ ( x = \ overline { OP } \ ) có phương trình là :
\ ( x = OMcos \ left ( { \ omega t + \ varphi } \ right ) \ )
Đặt OM = A, phương trình của tọa độ x được viết thành :
\ ( x = Acos \ left ( { \ omega t + \ varphi } \ right ) \ ) với \ ( A, \ omega, \ varphi \ ) là những hằng số .
⇒ Phương trình trên được gọi là phương trình của giao động điều hòa .
Trong đó :
+ x : li độ của vật
+ A : biên độ của vật ( giá trị lớn nhất của li độ )
+ \ ( \ left ( { \ omega t + \ varphi } \ right ) \ ) : là pha giao động tại thời gian t
+ \ ( \ varphi \ ) : là pha bắt đầu của xê dịch
III – Chu kì, tần số, tần số góc của dao động điều hòa
1. Chu kì
– Chu kì của giao động điều hòa là khoảng chừng thời hạn để vật thực thi một xê dịch toàn phần .
– Kí hiệu : T
– Đơn vị : giây ( s )
2. Tần số
– Tần số của giao động điều hòa là số xê dịch toàn phần thực thi được trong một giây .
– Kí hiệu : f
– Đơn vị : Hz
3. Tần số góc:
– Trong giao động điều hòa \ ( \ omega \ ) được gọi là tần số góc :
\ ( \ omega = \ frac { { 2 pi } } { T } = 2 \ pi f \ )
– Đơn vị : rad / s
IV – Vận tốc và gia tốc của dao động điều hòa
1. Vận tốc
– Vận tốc là đạo hàm của li độ theo thời hạn .
\ ( v = x ’ = – \ omega Asin \ left ( { \ omega t + \ varphi } \ right ) \ )
– Vận tốc là đại lượng biến thiên điều hòa :
+ Ở vị trí biên \ ( x = \ pm A \ ) tốc độ bằng 0
+ Ở vị trí cân đối x = 0 thì tốc độ cực lớn \ ( { v_ { max } } = \ omega A \ )
2. Gia tốc
– Gia tốc là đạo hàm của tốc độ theo thời hạn
\ ( a = v ’ = – { \ omega ^ 2 } Acos \ left ( { \ omega t + \ varphi } \ right ) = – { \ omega ^ 2 } x \ )
Tại vị trí cân đối x = 0 ⇒ a = 0 và hợp lực F = 0 .
Gia tốc luôn ngược dấu với li độ ( hay vectơ tần suất luôn hướng về vị trí cân đối ) và có độ lớn tỉ lệ với độ lớn của li độ .
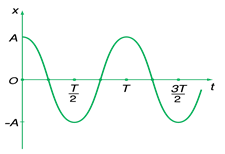
V – Đồ thị của dao động điều hòa
Đồ thị của xê dịch điều hòa là một đường hình sin .
CÂU HỎI (C)
Trả lời câu hỏi C1 trang 5 Vật Lý 12
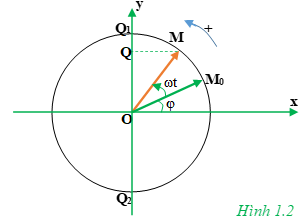
Gọi Q. là hình chiếu của điểm M lên trục y ( H. 1.2 ). Chứng minh rằng điểm Q. giao động điều hòa .
Trả lời:
Gọi Q. là hình chiếu của điểm M lên trục Oy
Ta có tọa độ y = OQ của điểm Q. có phương trình là :
yQ = OMsin ( ωt + φ )
Đặt OM = A, phương trình tọa độ y được viết lại là :
yQ = Asin ( ωt + φ )
Vì hàm sin hay cosin là một xê dịch điều hòa, nên xê dịch của điểm Q. được gọi là xê dịch điều hòa .
CÂU HỎI VÀ BÀI TẬP
Dưới đây là phần Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 8 9 sgk Vật Lí 12 vừa đủ và ngắn gọn nhất. Nội dung cụ thể bài giải ( câu vấn đáp ) những câu hỏi và bài tập những bạn xem sau đây :
❓
1. Giải bài 1 trang 8 Vật Lý 12
Phát biểu định nghĩa của xê dịch điều hòa .
Trả lời:
Dao động điều hòa là xê dịch trong đó li độ của vật là một hàm cosin ( hay sin ) của thời hạn .
Phương trình x = Acos ( ωt + φ ) được gọi là phương trình của xê dịch điều hòa .
2. Giải bài 2 trang 8 Vật Lý 12
Viết phương trình của xê dịch điều hòa và lý giải những đại lượng trong phương trình .
Trả lời:
Phương trình xê dịch điều hòa là \ ( x = Acos ( ωt + φ ) \ ), trong đó :
– \ ( x \ ) : là li độ của xê dịch, có đơn vị chức năng là centimet hoặc mét ( cm ; m )
– \ ( A \ ) : là biên độ giao động, có đơn vị chức năng là centimet hoặc mét ( cm ; m )
– \ ( ω \ ) : là tần số góc của giao động, có đơn vị chức năng là ( rad / s )
– \ ( ( ωt + φ ) \ ) : là pha của xê dịch tại thời gian t, có đơn vị chức năng là radian ( rad )
– \ ( φ \ ) : là pha khởi đầu của giao động, có đơn vị chức năng là radian ( rad )
3. Giải bài 3 trang 8 Vật Lý 12
Mối liên hệ giữa giao động điều hòa và hoạt động tròn bộc lộ ở chỗ nào ?
Trả lời:
Một điểm dao động điều hòa trên một đoạn thẳng luôn luôn có thể được coi là hình chiếu của một điểm tương ứng chuyển động tròn đều lên đường kính là đoạn thẳng đó.
4. Giải bài 4 trang 8 Vật Lý 12
Nêu định nghĩa chu kì và tần số của giao động điều hòa .
Trả lời:
Chu kì T của giao động điều hòa là khoảng chừng thời hạn để triển khai được một giao động toàn phần. Đơn vị của chu kì là giây ( s )
Tần số f của xê dịch điều hòa là số xê dịch toàn phần triển khai được trong một giây. Đơn vị của tần số là héc ( Hz )
5. Giải bài 5 trang 8 Vật Lý 12
Giữa chu kì, tần số và tần số góc có mối liên hệ như thế nào ?
Trả lời:
Tần số góc ω của giao động điều hòa là một đại lượng liên hệ với chu kì T hay với tần số f bằng những hệ thức sau đây :
ω = 2 π / T = 2 πf .
6. Giải bài 6 trang 8 Vật Lý 12
Một vật giao động điều hòa theo phương trình : x = Acos ( ωt + φ )
a. Lập công thức tính tốc độ và tần suất của vật
b ) Ở vị trí nào thì tốc độ bằng 0. Ở vị trí nào thì tần suất bằng 0 .
c ) Ở vị trí nào thì tốc độ có độ lớn cực lớn. Ở vị trí nào thì tần suất có độ lớn cực lớn .
Trả lời:
a) v = x’ = -ωAsin(ωt + φ)
a = v ’ = – ω2Acos ( ωt + φ ) = – ω2x
b) Ở vị trí biên thì vận tốc bằng 0. Tại vị trí cân bằng thì gia tốc bằng 0.
c ) Ở vị trí cân đối thì tốc độ có độ lớn cực lớn. Còn ở vị trí biên thì tần suất có độ lớn cực lớn .
?
1. Giải bài 7 trang 9 Vật Lý 12
Một vật xê dịch điều hòa có quỹ đạo là một đoạn thẳng dài 12 cm. Biên độ xê dịch của vật là bao nhiêu ?
A. 12 cm, B. – 12 cm .
C. 6 cm, D. – 6 cm .
Bài giải:
Ta có :
Chiều dài quỹ đạo : \ ( L = 12 cm = 2A \ )
→ Biên độ xê dịch của vật :
\ ( A = \ dfrac { L } { 2 } = \ dfrac { 12 } { 2 } = 6 cm \ )
⇒ Đáp án C.
2. Giải bài 8 trang 9 Vật Lý 12
Một vật hoạt động tròn đều với vận tốc góc là \ ( \ pi rad / s \ ). Hình chiếu của vật trên một đường kính xê dịch điều hòa với tần số góc, chu kì và tần số bằng bao nhiêu ?
A. \ ( \ pi rad / s ; 2 s ; 0,5 Hz \ )
B. \ ( 2 \ pi rad / s ; 0,5 s ; 2 Hz \ )
C. \ ( 2 \ pi rad / s ; 1 s ; 1 Hz \ )
D. \ ( \ dfrac { \ pi } { 2 } rad / s ; 4 s ; 0,25 Hz \ )
Bài giải:
Ta có :
Tốc độ góc của vật hoạt động tròn cũng chính là tần số góc của vật : \ ( \ omega = \ pi ( rad / s ) \ )
Chu kì đao động của vật :
\ ( T = \ dfrac { 2 pi } { \ omega } = \ dfrac { 2 pi } { \ pi } = 2 s \ )
Tần số giao động của vật :
\ ( f = \ dfrac { 1 } { T } = \ dfrac { 1 } { 2 } = 0,5 Hz \ ) .
⇒ Đáp án A.
3. Giải bài 9 trang 9 Vật Lý 12
Cho phương trình của giao động điều hòa \ ( x = – 5 cos ( 4 πt ) ( cm ) \ ). Biên độ và pha bắt đầu của xê dịch là bao nhiêu ?
A. 5 cm ; 0 rad .
B. 5 cm ; 4 π rad .
C. 5 cm ; ( 4 πt ) rad .
D. 5 cm ; π rad .
Bài giải:
Ta có, phương trình giao động :
\ ( x = – 5 cos ( 4 \ pi t ) = 5 cos ( 4 \ pi t + \ pi ) cm \ )
So sánh với phương trình tổng quát \ ( x = Acos ( \ omega t + \ varphi ) \ )
→ Biên độ của giao động \ ( A = 5 cm \ ), pha bắt đầu \ ( \ varphi = \ pi rad \ )
⇒ Đáp án D.
4. Giải bài 10 trang 9 Vật Lý 12
Phương trình của giao động điều hòa là x = 2 cos ( 5 t – \ ( \ frac { \ pi } { 6 } ) \ ) ( cm ). Hãy cho biết biên độ, pha bắt đầu, và pha ở thời gian t của giao động .
Bài giải:
Phương trình : x = 2 cos ( 5 t – \ ( \ frac { \ pi } { 6 } ) \ ) cm
Biên độ : A = 2 cm
Pha ban đầu : φ = – \ ( \ frac { \ pi } { 6 } \ ) ( rad )
Pha giao động ở thời gian t : \ ( 5 t – ( \ frac { \ pi } { 6 } ) \ ) ( rad )
5. Giải bài 11 trang 9 Vật Lý 12
Một vật hoạt động điều hòa phải mất 0,25 s để đi từ điểm có tốc độ bằng 0 tới điểm tiếp theo cũng có tốc độ bằng 0. Khoảng cách giữa hai điểm là 36 cm. Tính :
a ) Chu kì .
b ) Tần số .
c ) Biên độ .
Bài giải:
Ta có :
\(\eqalign{
& {{{x^2}} \over {{A^2}}} + {{{v^2}} \over {{\omega ^2}{A^2}}} = 1 \Rightarrow v = \pm \omega \sqrt {{A^2} – {x^2}} \cr
& → v = 0 \Leftrightarrow \omega \sqrt {{A^2} – {x^2}} = 0 → x = A \cr} \)
⇒ tốc độ bằng 0 khi vật đi qua vị trí biên .
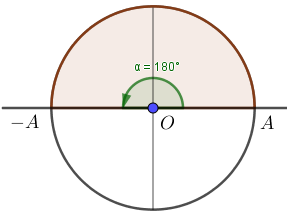
Góc mà vật quét được khi đi từ biên này sang biên kia là \ ( \ Delta \ varphi = 180 ^ 0 = \ pi = \ omega \ Delta t \ )
⇒ Khoảng thời hạn giữa hai lần liên tục tốc độ bằng 0 ( vật đi từ biên này đến biên kia ) là \ ( \ Delta t = \ dfrac { \ Delta \ varphi } { \ omega } = \ dfrac { \ pi } { \ dfrac { 2 \ pi } { T } } = \ dfrac { T } { 2 } = 0,25 s \ ) và khoảng cách giữa hai biên bằng \ ( 2A = 36 cm \ )
a) Ta suy ra chu kì dao động của vật: \(T = 2.0,25=0,5s\)
b) Tần số dao động của vật: \(f=\dfrac{1 }{T}=\dfrac{1}{0,5}=2Hz\)
c) Biên độ dao động của vật: \(A =\dfrac{36}{2}= 18cm\)
Bài tiếp theo:
Xem thêm :
Trên đây là phần Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 8 9 sgk Vật Lí 12 vừa đủ, ngắn gọn và dễ hiểu nhất. Chúc những bạn làm bài môn Vật lý 12 tốt nhất !
“ Bài tập nào khó đã có giaibaisgk.com “
Source: https://futurelink.edu.vn
Category: Tin tổng hợp