Tìm m để hàm số đồng biến trên khoảng nghịch biến trên khoảng là bài toán xuất hiện nhiều trong các đề thi THPTQG và trong các đề thi thử của các trường trên toàn quốc. Vậy làm thế nào để ôn tập và làm tốt dạng toán này? Bài viết dưới đây tôi sẽ hướng dẫn các bạn cách để tư duy đối với dạng toán này. Đồng thời cũng chỉ cho các bạn một số phương pháp theo thứ tự ưu tiên để giải toán. Đọc bài viết để tìm hiểu thêm nhé.
Tham gia Group để nhận được nhiều tài liệu cực xịn và hỗ trợ miễn phí từ mình: Click here!
I. PHƯƠNG PHÁP TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN NGHỊCH BIẾN TRÊN KHOẢNG
Bài toán: Cho hàm số f(x,m) xác định và có đạo hàm trên khoảng (a;b). Tìm giá trị của m để hàm số f(x,m) đơn điệu trên khoảng (a;b).
1. PHƯƠNG PHÁP GIẢI BÀI TOÁN TÌM M ĐỂ HÀM SỐ ĐƠN ĐIỆU TRÊN KHOẢNG
Trước hết ta đã có định lý sau: Cho hàm số f(x) có đạo hàm trên khoảng (a;b).
Hàm số f ( x ) đồng biến trên khoảng ( a ; b ) khi và chỉ khi f ‘ ( x ) ≥ 0 với mọi giá trị x thuộc khoảng ( a ; b ). Dấu = chỉ được xảy ra tại hữu hạn điểm .
Tương tự, hàm số f ( x ) nghịch biến trên khoảng ( a ; b ) khi và chỉ khi f ‘ ( x ) ≤ 0 với mọi giá trị x thuộc khoảng ( a ; b ). Dấu = chỉ được xảy ra tại hữu hạn điểm .
Như vậy muốn hàm số f ( x ) có đạo hàm trên khoảng ( a ; b ) thì f ( x ) cần phải xác lập và liên tục trên khoảng ( a ; b ) .
Do đó để xử lý bài toán tìm m để hàm số đồng biến trên khoảng cho trước hay tìm m để hàm số nghịch biến trên khoảng cho trước thì ta nên triển khai theo thứ tự như sau :
-
Kiểm tra tập xác định:
Vì bài toán có tham số nên ta cần tìm điều kiện của tham số để hàm số xác định trên khoảng (a;b).
-
Tính đạo hàm và tìm điều kiện của tham số để đạo hàm không âm (âm) hoặc không dương (dương) trên khoảng (a;b):
Theo định lý trên chúng ta cần xét dấu của đạo hàm trên khoảng (a;b). Do đó đương nhiên chúng ta phải tính đạo hàm.
2. PHƯƠNG PHÁP ĐÁNH GIÁ ĐẠO HÀM KHI CÓ THAM SỐ
Đến bước này những bạn cần đưa ra sự lựa chọn giải pháp nhìn nhận đạo hàm. Theo thứ tự những bạn nên ưu tiên như sau :
-
Nhẩm nghiệm của đạo hàm:
Hiển nhiên, nếu đạo hàm có nghiệm đặc biệt hoặc biết được hết các nghiệm thì ta dễ dàng xét được dấu của nó rồi. Nên ta phải ưu tiên cách này trước.
- Cô lập tham số m :
Cô lập được tham số m từ bất phương trình f ‘ ( x, m ) ≥ 0 với mọi x thuộc khoảng ( a ; b ) ví dụ điển hình. Ta sẽ thu được bất phương trình dạng m ≥ g ( x )
với mọi x thuộc khoảng (a;b). Hoặc m≤g(x) với mọi x thuộc khoảng (a;b). Khi đó, hãy chú ý rằng nếu g(x) có giá trị lớn nhất hay nhỏ nhất thì:
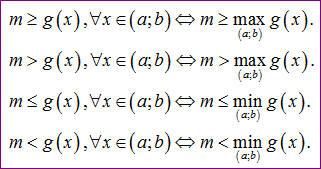Còn trong trường hợp không có giá trị lớn nhất hay nhỏ nhất thì ta có thể xét đến cận trên đúng hoặc cận dưới đúng của g(x). Và lúc này dấu = cần xem xét cẩn thận. -
Dùng kiến thức về nghiệm và dấu của tam thức bậc 2:
Hai cách trên không sử dụng được nữa thì ta phải áp dụng các kiến thức về nghiệm và dấu của tam thức bậc 2 vào giải quyết.
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
II. VÍ DỤ TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN TRÊN KHOẢNG NGHỊCH BIẾN TRÊN KHOẢNG
1. TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN TRÊN R NGHỊCH BIẾN TRÊN R
Trong chương trình, đây là dạng toán thường gặp so với hàm số đa thức bậc 3. Nếu là hàm đa thức bậc 3 thì tất cả chúng ta hoàn toàn có thể vận dụng kiến thức và kỹ năng sau :
Ví dụ:
Lời giải:
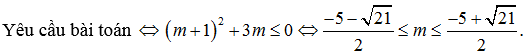
2. TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN NGHỊCH BIẾN TRÊN TỪNG KHOẢNG XÁC ĐỊNH
Trong chương trình đại trà phổ thông ta thường gặp dạng toán này ở hàm phân tuyến tính ( hay hàm số phân thức bậc 1 trên bậc 1 ). Đối với hàm số này ta hoàn toàn có thể vận dụng kỹ năng và kiến thức sau :
Ví dụ:
Lời giải:
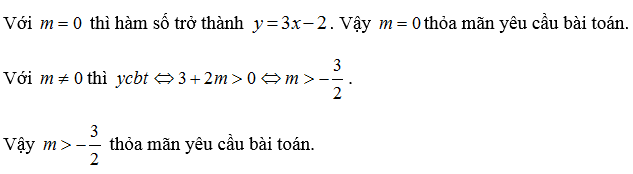
3. VÍ DỤ VỀ NHẨM ĐƯỢC NGHIỆM CỦA ĐẠO HÀM
Ví dụ:
Cho hàm số y = x³ – ( m + 1 ) x² – ( m²-2m ) x + 2020. Tìm m để hàm số nghịch biến trên khoảng ( 0 ; 1 ) .
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
4. VÍ DỤ VỀ CÔ LẬP THAM SỐ M
Ví dụ:
Cho hàm số y = x³ + mx² + 2 mx + 3. Tìm điều kiện kèm theo của m để hàm số đồng biến trên khoảng ( 0 ; 2 ) .
Lời giải:
5. VÍ DỤ VỀ HÀM PHÂN TUYẾN TÍNH ĐƠN ĐIỆU TRÊN KHOẢNG CHO TRƯỚC
Với hàm số phân tuyến tính có tham số, những bạn cần quan tâm đến những trường hợp hàm số suy biến. Cụ thể ta cần xét trường hợp hàm số suy biến thành hàm bậc nhất ( nếu có ). Còn trường hợp hàm suy biến thành hằng thì không cần xét vì trong trường hợp này hàm số cũng không phải hàm đơn điệu. Sau khi xét xong trường hợp suy biến ( nếu có ) thì những bạn hoàn toàn có thể sử dụng kiến thức và kỹ năng sau để giải toán .
Ví dụ 1:
Lời giải:
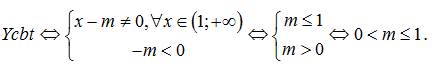
Ví dụ 2:
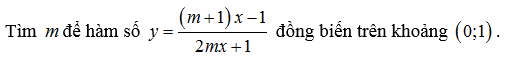
Lời giải:
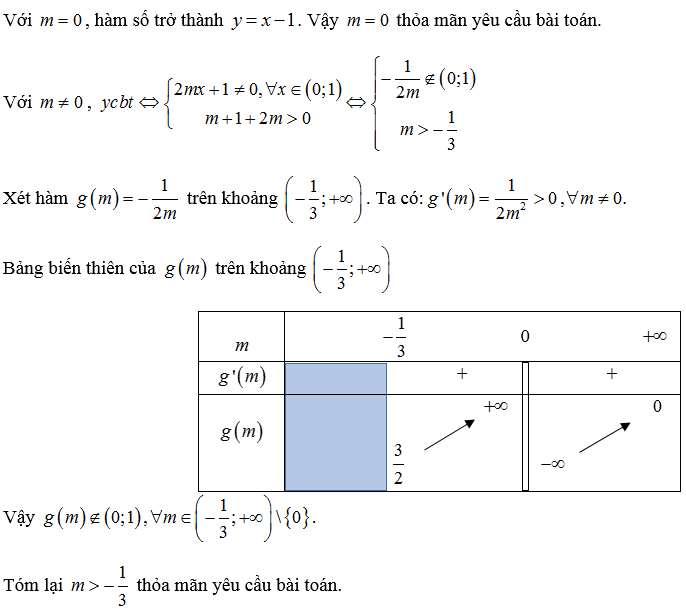
Trên đây là phương pháp và một số ví dụ về tìm giá trị tham số m để hàm số đơn điệu trên một khoảng cho trước. Chúc các bạn học giỏi và thành công.
Xem thêm :
Tính đơn điệu của hàm số là gì?
Hàm số –
Source: https://futurelink.edu.vn
Category: Tin tổng hợp