Lý thuyết
1. §1. Các định nghĩa
2. §2. Tổng và hiệu của hai vectơ
3. §3. Tích của vectơ với một số
4. §4. Hệ trục tọa độ
Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 27 28 sgk Hình học 10. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé !
Bài tập
Giaibaisgk. com ra mắt với những bạn rất đầy đủ chiêu thức giải bài tập hình học 10 kèm bài giải cụ thể bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 27 28 sgk Hình học 10 của Bài Ôn tập Chương I. Vectơ cho những bạn tìm hiểu thêm. Nội dung cụ thể bài giải từng bài tập những bạn xem dưới đây :

1. Giải bài 1 trang 27 sgk Hình học 10
Cho lục giác đều $ ABCDEF $ tâm USD O USD. Hãy chỉ ra những vectơ bằng vectơ $ AB $ có điểm đầu và điểm cuối là $ O USD hoặc những đỉnh của lục giác .
Bài giải:
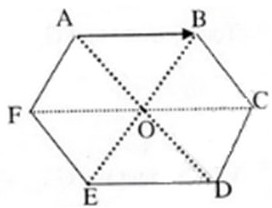
Các vectơ bằng vectơ $ AB $ có điểm đầu và điểm cuối là $ O USD hoặc những đỉnh của lục giác là :
USD \ overrightarrow { OC } ; \ overrightarrow { FO } ; \ overrightarrow { ED } $
2. Giải bài 2 trang 27 sgk Hình học 10
Cho hai vectơ $ \ overrightarrow { a } ; \ overrightarrow { b } $ đều khác $ \ overrightarrow { 0 } $. Các khẳng định chắc chắn sau đúng hay sai ?
a ) Hai vectơ $ \ overrightarrow { a } ; \ overrightarrow { b } $ cùng hướng thì cùng phương .
b ) Hai vectơ $ \ overrightarrow { b } ; k \ overrightarrow { b } $ cùng phương .
c ) Hai vectơ $ \ overrightarrow { a } ; ( – 2 ) \ overrightarrow { a } $ cùng hướng .
d ) Hai vectưo $ \ overrightarrow { a } ; \ overrightarrow { b } $ ngược hướng với vectơ thứ ba khác $ \ overrightarrow { 0 } $ thì cùng phương .
Trả lời:
Áp dụng kim chỉ nan kiến thức và kỹ năng về tọa độ trong vectơ, ta có :
a) Đúng, vì ta chỉ xét các vectơ cùng hướng hay ngược hướng khi các vectơ này cùng phương.
b) Đúng (theo định nghĩa tích của một số với một vectơ)
c) Sai, \(\overrightarrow a \) và \(( – 2)\overrightarrow a \) là hai vectơ ngược hướng
d) Đúng vì \(\overrightarrow a \uparrow \downarrow \overrightarrow c ,\;\;\overrightarrow b \uparrow \downarrow \overrightarrow c \Rightarrow \overrightarrow a \uparrow \uparrow \overrightarrow b .\)
3. Giải bài 3 trang 27 sgk Hình học 10
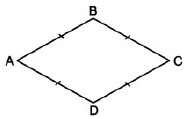
Tứ giác $ ABCD $ là hình gì nếu $ \ overrightarrow { AB } = \ overrightarrow { DC } $ và $ \ left | \ overrightarrow { AB } \ right | = \ left | \ overrightarrow { BC } \ right | $
Bài giải:
Ta có : \ ( \ overrightarrow { AB } = \ overrightarrow { DC } \ ) suy ra \ ( AB / / DC \ ) và \ ( AB = DC \ ) do đó \ ( ABCD \ ) là hình bình hành .
\ ( | \ overrightarrow { AB } | = | \ overrightarrow { BC } | \ ) suy ra \ ( AB = BC \ ), hình bình hành \ ( ABCD \ ) có \ ( 2 \ ) cạnh liên tục bằng nhau do đó \ ( ABCD \ ) là hình thoi ( theo tín hiệu phân biệt hình thoi ) .
4. Giải bài 4 trang 27 sgk Hình học 10
Chứng minh rằng : $ \ left | \ overrightarrow { a } + \ overrightarrow { b } \ right | \ leq \ left | \ overrightarrow { a } \ right | + \ left | \ overrightarrow { b } \ right | $
Bài giải:
♦ TH1 : Khi $ \ overrightarrow { a } $, $ \ overrightarrow { b } $ cùng phương
⇒ $ \ overrightarrow { a } = k \ overrightarrow { b } $
USD \ left | \ overrightarrow { a } \ right | = k \ left | \ overrightarrow { b } \ right | $
⇒ $ \ left | \ overrightarrow { a } + \ overrightarrow { b } \ right | \ leq \ left | \ overrightarrow { a } \ right | + \ left | \ overrightarrow { b } \ right | $ ( đpcm )
♦ TH2 : Khi $ \ overrightarrow { a } $, $ \ overrightarrow { b } $ không cùng phương

⇒ $ \ left | \ overrightarrow { a } + \ overrightarrow { b } \ right | \ leq \ left | \ overrightarrow { a } \ right | + \ left | \ overrightarrow { b } \ right | $ ( đpcm )
5. Giải bài 5 trang 27 sgk Hình học 10
Cho tam giác đều $ ABC $ nội tiếp đường tròn tâm USD O USD. Hãy xác lập những điểm USD M, N, P $ sao cho :
a ) $ \ overrightarrow { OM } = \ overrightarrow { OA } + \ overrightarrow { OB } $
b ) $ \ overrightarrow { ON } = \ overrightarrow { OB } + \ overrightarrow { OC } $
c ) $ \ overrightarrow { OP } = \ overrightarrow { OC } + \ overrightarrow { OA } $
Bài giải:
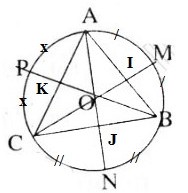
Gọi USD I, J, K $ lần lượt là trung điểm của những cạnh $ AB, BC $ và $ AC $ của tam giác đều $ ABC. $
a) Gọi $M$ là trung điểm của cung nhỏ $AB$
⇒ $ \ overrightarrow { OM } = 2 \ overrightarrow { OI } $
Mặt khác : $ \ overrightarrow { OA } + \ overrightarrow { OB } = 2 \ overrightarrow { OI } $
⇒ $ \ overrightarrow { OM } = \ overrightarrow { OA } + \ overrightarrow { OB } $ ( đpcm )
b) Gọi $N$ là trung điểm của cung nhỏ $BC$
⇒ $ \ overrightarrow { ON } = 2 \ overrightarrow { OJ } $
Mặt khác : $ \ overrightarrow { OB } + \ overrightarrow { OC } = 2 \ overrightarrow { OJ } $
⇒ $ \ overrightarrow { ON } = \ overrightarrow { OB } + \ overrightarrow { OC } $ ( đpcm )
c) Gọi $P$ là trung điểm của cung nhỏ $AC.$
⇒ $ \ overrightarrow { OP } = 2 \ overrightarrow { OK } $
Mặt khác : $ \ overrightarrow { OC } + \ overrightarrow { OA } = 2 \ overrightarrow { OK } $
⇒ $ \ overrightarrow { OP } = \ overrightarrow { OC } + \ overrightarrow { OA } $ ( đpcm )
6. Giải bài 6 trang 27 sgk Hình học 10
Cho tam giác đều $ ABC $ có cạnh bằng USD a USD. Tính :
a ) $ \ left | \ overrightarrow { AB } + \ overrightarrow { AC } \ right | $
b ) $ \ left | \ overrightarrow { AB } – \ overrightarrow { AC } \ right | $
Bài giải:

a) Từ $A$ vẽ đường cao $AH$, ta có:
USD \ overrightarrow { AB } + \ overrightarrow { AC } = 2 \ overrightarrow { AH } $
Mà $ \ overrightarrow { AH } = A \ frac { \ sqrt { 3 } } { 2 } $
⇒ $ \ left | \ overrightarrow { AB } + \ overrightarrow { AC } \ right | = 2 \ frac { a \ sqrt { 3 } } { 2 } = a \ sqrt { 3 } $
b) Theo bài ra: $\overrightarrow{AB}-\overrightarrow{AC} |$
= $ \ overrightarrow { AB } + \ overrightarrow { CA } = \ overrightarrow { CB } $
⇒ $ \ left | \ overrightarrow { AB } – \ overrightarrow { AC } \ right | = \ overrightarrow { CB } = a $ .
7. Giải bài 7 trang 28 sgk Hình học 10
Cho sáu điểm USD M, N, P., Q., R, S $ bất kể. Chứng minh rằng :
\ ( \ overrightarrow { MP } + \ overrightarrow { NQ } + \ overrightarrow { RS } = \ overrightarrow { MS } + \ overrightarrow { NP } + \ overrightarrow { RQ } \ )
Bài giải:
Ta có :
\(\eqalign{
& \overrightarrow {MP} = \overrightarrow {MS} + \overrightarrow {SP} \cr
& \overrightarrow {NQ} = \overrightarrow {NP} + \overrightarrow {PQ} \cr
& \overrightarrow {RS} = \overrightarrow {RQ} + \overrightarrow {QS} \cr
& \Rightarrow \overrightarrow {MP} + \overrightarrow {PQ} + \overrightarrow {RS} = (\overrightarrow {MS} + \overrightarrow {NP} + \overrightarrow {RQ} ) + (\overrightarrow {SP} + \overrightarrow {PQ} + \overrightarrow {QS} ) \cr} \)
Vì \ ( \ overrightarrow { SP } + \ overrightarrow { PQ } + \ overrightarrow { QS } = \ overrightarrow { SS } = \ overrightarrow 0 \ )
Từ đó suy ra điều phải chứng tỏ .
8. Giải bài 8 trang 28 sgk Hình học 10
Cho tam giác USD OAB USD. Gọi USD M $ và $ N $ lần lượt là trung điểm của $ OA $ và USD OB USD. Tìm những số USD M, N $ sao cho :
a ) \ ( \ overrightarrow { OM } = m \ overrightarrow { OA } + n \ overrightarrow { OB } \ )
b ) \ ( \ overrightarrow { AN } = m \ overrightarrow { OA } + n \ overrightarrow { OB } \ )
c ) \ ( \ overrightarrow { MN } = m \ overrightarrow { OA } + n \ overrightarrow { OB } \ )
d ) \ ( \ overrightarrow { MB } = m \ overrightarrow { OA } + n \ overrightarrow { OB } \ )
Bài giải:
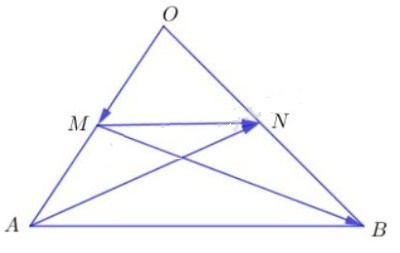
a) Ta có: \(\overrightarrow {OM} = {1 \over 2}\overrightarrow {OA} \)
Do đó : \ ( m = { 1 \ over 2 } ; n = 0 \ )
b) Ta có: vì N là trung điểm OB
\(\eqalign{
& 2\overrightarrow {AN} = \overrightarrow {AO} + \overrightarrow {AB} \cr
& \Rightarrow 2\overrightarrow {AN} = \overrightarrow {AO} + \overrightarrow {AO} + \overrightarrow {OB} \cr
& \Rightarrow 2\overrightarrow {AN} = 2\overrightarrow {AO} + \overrightarrow {OB} \Rightarrow \overrightarrow {AN} = – \overrightarrow {OA} + {1 \over 2}\overrightarrow {OB} \cr} \)
Vậy \ ( m = – 1 ; n = { 1 \ over 2 } \ )
c) Ta có:
\(\eqalign{
& \overrightarrow {MN} = {1 \over 2}\overrightarrow {AB} \Rightarrow \overrightarrow {MN} = {1 \over 2}(\overrightarrow {AO} + \overrightarrow {OB} ) \cr
& \Rightarrow \overrightarrow {MN} = – {1 \over 2}\overrightarrow {OA} + {1 \over 2}\overrightarrow {OB} \cr} \)
Vậy \ ( m = – { 1 \ over 2 }, n = { 1 \ over 2 } \ )
d) Ta có:
\(\eqalign{
& 2\overrightarrow {BM} = \overrightarrow {BA} + \overrightarrow {BO} \Rightarrow 2\overrightarrow {BM} = \overrightarrow {BO} + \overrightarrow {OA} + \overrightarrow {BO} \cr
& \Rightarrow 2\overrightarrow {BM} = 2\overrightarrow {BO} + \overrightarrow {OA} \Rightarrow 2\overrightarrow {MB} = – \overrightarrow {OA} + 2\overrightarrow {OB} \cr
& \Rightarrow \overrightarrow {MB} = – {1 \over 2}\overrightarrow {OA} + \overrightarrow {OB} \cr} \)
Vậy \ ( m = – { 1 \ over 2 }, n = 1 \ )
9. Giải bài 9 trang 28 sgk Hình học 10
Chứng minh rằng nếu USD G $ và USD G ’ $ lần lượt là trọng tâm của những tam giác $ ABC $ và $ A’B ’ C ’ $ bất kể thì :
\ ( 3 \ overrightarrow { GG ’ } = \ overrightarrow { AA ’ } + \ overrightarrow { BB ’ } + \ overrightarrow { CC ’ } \ )
Bài giải:
Ta có :
\(\eqalign{
& \overrightarrow {GG’} = \overrightarrow {GA} + \overrightarrow {AA’} + \overrightarrow {B’G’} \cr
& \overrightarrow {GG’} = \overrightarrow {GB} + \overrightarrow {BB’} + \overrightarrow {B’G’} \cr
& \overrightarrow {GG’} = \overrightarrow {GC} + \overrightarrow {CC’} + \overrightarrow {C’G’} \cr
& \Rightarrow 3\overrightarrow {GG’} = (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} ) + (\overrightarrow {AA’} + \overrightarrow {BB’} + \overrightarrow {CC’} ) + (\overrightarrow {A’G’} + \overrightarrow {B’G’} + \overrightarrow {C’G’} )(1) \cr} \)
USD G $ là trọng tâm của tam giác $ ABC $ nên :
\ ( \ overrightarrow { GA } + \ overrightarrow { GB } + \ overrightarrow { GC } = \ overrightarrow 0 \ ) ( 2 )
USD G ’ $ là trọng tâm của tam giác USD A’B ’ C ’ $ nên :
\(\eqalign{
& \overrightarrow {G’A’} + \overrightarrow {G’B’} + \overrightarrow {G’C’} = \overrightarrow 0 \cr
& \Leftrightarrow \overrightarrow {A’G’} + \overrightarrow {B’G’} + \overrightarrow {C’G’} = \overrightarrow 0 \cr} \)
( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) suy ra \ ( 3 \ overrightarrow { GG ’ } = \ overrightarrow { AA ’ } + \ overrightarrow { BB ’ } + \ overrightarrow { CC ’ } \ ) ( đpcm )
10. Giải bài 10 trang 28 sgk Hình học 10
Trong mặt phẳng tọa độ $ Oxy $, những chứng minh và khẳng định sau đúng hay sai ?
a ) Hai vectơ đối nhau thì chúng có hoành độ đối nhau
b ) Vectơ \ ( \ overrightarrow a \ ) cùng phương với \ ( \ overrightarrow i \ ) nếu a có hoành độ bằng 0
c ) Vectơ \ ( \ overrightarrow i \ ) có hoành độ bằng 0 thì cùng phương với \ ( \ overrightarrow j \ )
Trả lời:
a) Trong mặt phẳng tọa độ $Oxy$ cho vectơ \(\overrightarrow a \) = (a1, a2) và vecto đối của vecto \(\overrightarrow a \) là vecto \(\overrightarrow b \)= – \(\overrightarrow a \) = (-a1, -a2).
Vậy chứng minh và khẳng định hai vectơ đối nhau thì chúng có hoành độ đối nhau là đúng .
b) Trong mặt phẳng tọa độ $Oxy$, vectơ \(\overrightarrow i \) (1, 0):
Vectơ \ ( \ overrightarrow a \ ) $ ≠ 0 USD cùng phương với vectơ \ ( \ overrightarrow i \ ) khi \ ( \ overrightarrow a = k \ overrightarrow i \ ) với USD k ∈ R. $
Suy ra : \ ( \ overrightarrow a \ ) $ = ( k, 0 ) USD với USD k ≠ 0. $
Vậy chứng minh và khẳng định vectơ USD a ≠ 0 USD cùng phương với vectơ nếu có hoành độ bằng USD 0 $ là sai .
c) Trong mặt phẳng $Oxy$ có vecto $(0, 1)$
Vectơ \ ( \ overrightarrow a \ ) cùng phương với vectơ \ ( \ overrightarrow j \ ) khi \ ( \ overrightarrow a \ ) = k \ ( \ overrightarrow j \ ) với USD k ∈ R. $
Suy ra : \ ( \ overrightarrow a \ ) USD = ( 0, k ) USD với USD k ∈ R. $
Vậy chứng minh và khẳng định vectơ \ ( \ overrightarrow a \ ) có hoành độ bằng USD 0 USD thì cùng phương với \ ( \ overrightarrow j \ ) là đúng .
11. Giải bài 11 trang 28 sgk Hình học 10
Cho \ ( \ overrightarrow a ( 2,1 ) ; \ overrightarrow b ( 3, – 4 ) ; \ overrightarrow c ( – 7,2 ) \ )
a ) Tìm tọa độ của vectơ \ ( \ overrightarrow u = 3 \ overrightarrow a + 2 \ overrightarrow b – 4 \ overrightarrow c \ )
b ) Tìm tọa độ vectơ x sao cho \ ( \ overrightarrow x + \ overrightarrow a = \ overrightarrow b – \ overrightarrow c \ )
c ) Tìm những số k và h sao cho \ ( \ overrightarrow c = k \ overrightarrow a + h \ overrightarrow b \ )
Bài giải:
a) Ta có:
\(\eqalign{
& \overrightarrow u = (3.2 + 2.3 – 4.( – 7);3.1 + 2( – 4) – 4.2) \cr
& \Rightarrow \overrightarrow u = (40, – 13) \cr} \)
b) Gọi tọa độ của x là (m, n). Ta có:
\(\eqalign{
& \overrightarrow x + \overrightarrow a = (m + 2,n – 1) \cr
& \overrightarrow b – \overrightarrow c = ( – 10,6) \cr} \)
Giải hệ phương trình :
\(\eqalign{
& \left\{ \matrix{
m + 2 = 10 \hfill \cr
n + 1 = – 6 \hfill \cr} \right. \Rightarrow m = 8,n = 7 \cr
& \Rightarrow \overrightarrow x = (8, – 7) \cr} \)
c) Ta có: \(\overrightarrow c = k\overrightarrow a + h\overrightarrow b \Rightarrow \overrightarrow c = (2k + 3h;k – 4)\)
Với ta có hệ phương trình :
\(\left\{ \matrix{
2k + 3h = – 7 \hfill \cr
k – 4h = 2 \hfill \cr} \right.\)
Giải hệ phương trình này ta được : USD k = – 2, h = – 1 USD
12. Giải bài 12 trang 28 sgk Hình học 10
Cho :
\ ( \ overrightarrow u = { 1 \ over 2 } \ overrightarrow i – 5 \ overrightarrow j, \ overrightarrow v = \ overrightarrow { mi } – 4 \ overrightarrow j \ )
Tìm m để \ ( \ overrightarrow u \ ) và \ ( \ overrightarrow v \ ) cùng phương .
Bài giải:
Ta có :
\(\eqalign{
& \overrightarrow u = {1 \over 2}\overrightarrow i – 5\overrightarrow j \Rightarrow \overrightarrow u = ({1 \over 2}; – 5) \cr
& \overrightarrow v = m\overrightarrow i – 4\overrightarrow j \Rightarrow \overrightarrow v = (m, – 4) \cr} \)
Để thỏa mãn nhu cầu nhu yếu của đề bài :
\(\overrightarrow u //\overrightarrow v \Leftrightarrow \overrightarrow u = k\overrightarrow v \Leftrightarrow \left\{ \matrix{
{1 \over 2} = km \hfill \cr
– 5 = – 4k \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
m = {2 \over 5} \hfill \cr
k = {5 \over 4} \hfill \cr} \right. \Rightarrow m = {2 \over 5}\)
13. Giải bài 13 trang 28 sgk Hình học 10
Trong những khẳng định chắc chắn sau, khẳng định chắc chắn nào là đúng ?
a ) Điểm $ A $ nằm trên trục hoành thì có hoành độ bằng USD 0 USD
b ) $ P $ là trung điểm của đoạn thẳng $ AB $ khi và chỉ khi hoành độ của $ P $ bằng trung bình cộng những hoành độ của $ A $ và $ B $ .
c ) Nếu tứ giác $ ABCD $ là hình bình hành thì trung bình cộng những tọa độ tương ứng của $ A $ và $ C $ bằng trung bình cộng những tọa độ tương ứng của $ B $ và USD D $ .
Trả lời:
a) Sai vì các điểm nằm trên trục hoành thì có tung độ bằng $0$.
b) Sai. Để $P$ là trung điểm của $AB$ thì phải có:
– Hoành độ của $ P $ bằng trung bình cộng những hoành độ của $ A $ và $ B $ .
– Tung độ của $ P $ bằng trung bình cộng những tung độ của $ A $ và $ B $ .
Thiếu một trong hai điều trên đây thì $ P $ chưa chắc là trung điểm của $ AB $ .
c) Đúng.
Vì trong trường hợp này tứ giác $ ABCD $ có hai đường chéo $ AC $ và $ BD $ cắt nhau tại trung điểm của mỗi đường .
Bài trước:
Bài tiếp theo:
Xem thêm :
Chúc những bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 27 28 sgk Hình học 10 !
“ Bài tập nào khó đã có giaibaisgk.com “
Source: https://futurelink.edu.vn
Category: Tin tổng hợp