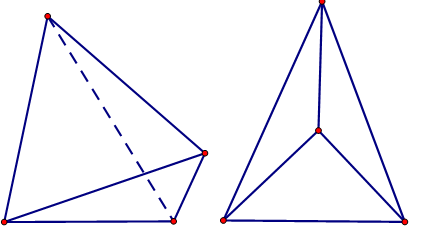
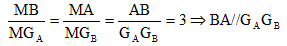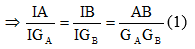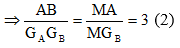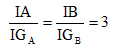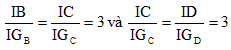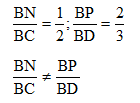Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 45: Hãy vẽ thêm một vài hình biểu diễn của hình chóp tam giác.
Lời giải
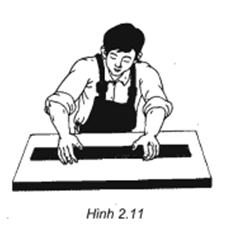
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 47: Tại sao người thợ mộc kiểm tra độ phẳng mặt bàn bằng cách rê thước trên mặt bàn? (h.2.11).
Lời giải
Theo đặc thù 3, nếu đường thẳng là 1 cạnh của thước có 2 điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường thẳng đó thuộc mặt phẳng bàn
Khi đó, nếu rê thước mà có 1 điểm thuộc cạnh thước nhưng không thuộc mặt bàn thì bàn đó chưa phẳng và ngược lại
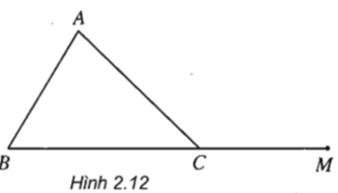
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 47: Cho tam giác ABC, M là điểm thuộc phần kéo dài của đoạn thẳng BC (h.2.12). Hãy cho biết M có thuộc mặt phẳng (ABC) không và đường thẳng AM có nằm trong mặt phẳng (ABC) không?
Lời giải
M ∈ BC mà BC ∈ ( ABC ) nên M ∈ ( ABC )
Vì A ∈ ( ABC ) nên mọi điểm thuộc AM đều thuộc ( ABC ) hay AM ∈ ( ABC )
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 48: Trong mặt phẳng (P), cho hình bình hành ABCD. Lấy điểm S nằm ngoài mặt phẳng (P). Hãy chỉ ra một điểm chung của hai mặt phẳng (SAC) và (SBD) khác điểm S (h.2.15).
Lời giải
Một điểm chung của hai mặt phẳng ( SAC ) và ( SBD ) khác điểm S là điểm I
I ∈ AC ∈ ( SAC )
I ∈ BD ∈ ( SBD )
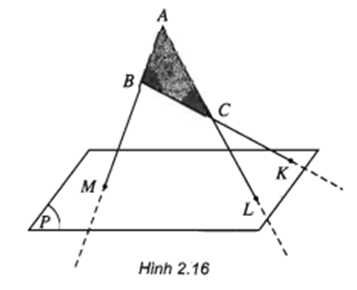
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 48: Hình 2.16 đúng hay sai? Tại sao?
Lời giải
Sai Vì theo đặc thù 2, có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng
Theo hình vẽ lại có : ba điểm không thẳng hàng M, L, K vừa thuộc ( ABC ), vừa thuộc ( P. ) ⇒ vô lý
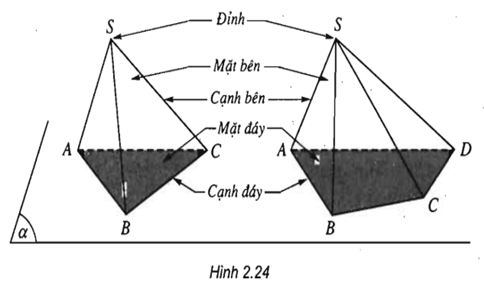
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 52: Kể tên các mặt bên, cạnh bên, cạnh đáy của hình chóp ở hình 2.24.
Lời giải
– Hình chóp tam giác :
Các mặt bên : ( SAB ), ( SBC ), ( SAC )
Các cạnh bên : SA, SB, SC
Các cạnh đáy : AB, AC, BC
– Hình chóp tứ giác :
Các mặt bên : ( SAB ), ( SBC ), ( SCD ), ( SAD )
Các cạnh bên : SA, SB, SC, SD
Các cạnh đáy : AB, BC, CD, DA
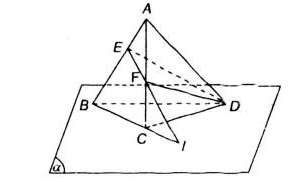
Bài 1 (trang 53 SGK Hình học 11): Cho điểm A không nằm trên mặt phẳng (α) chứa tam giác BCD. Lấy E và F là các điểm lần lượt nằm trên các cạnh AB, AC.
a ) Chứng minh đường thẳng EF nằm trong mặt phẳng ( ABC ) .
b ) Giả sử EF và BC cắt nhau tại I, chứng tỏ I là điểm chung của hai mặt phẳng ( BCD ) và ( DEF ) .
Lời giải:
a ) E ∈ AB mà AB ⊂ ( ABC )
=> E ∈ ( ABC )
F ∈ AC mà AC ⊂ ( ABC )
=> F ∈ ( ABC )
Đường thẳng EF có hai điểm E, F cùng thuộc mp ( ABC ) nên theo đặc thù 3 thì EF ⊂ ( ABC ) .
b ) I ∈ BC mà BC ⊂ ( BCD ) nên I ∈ ( BCD ) ( 1 )
I ∈ EF mà EF ⊂ ( DEF ) nên I ∈ ( DEF ) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra I là điểm chung của hai mặt phẳng ( BCD ) và ( DEF ) .
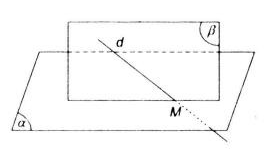
Bài 2 (trang 53 SGK Hình học 11): Gọi M là giao điểm của đường thẳng d và mặt phẳng (α). Chứng minh M là điểm chung của (α) với bất kì mặt phẳng nào chứa d.
Lời giải:
M là điểm chung của d và ( α ) nên :
M ∈ ( α ) ( 1 )
Một mặt phẳng bất kỳ ( P. ) chứa d thì M ∈ d mà d ⊂ ( P. ) nên :
M ∈ ( P. ) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra M là điểm chung của
( α ) và ( P. ) .
Bài 3 (trang 53 SGK Hình học 11): Cho ba đường thẳng d1, d2, d3 không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy.
Lời giải:
Gọi I = d1 ∩ d2
Giả sử d3 không qua I :
Khi đó phải cắt d1, d2 lần lượt tại M, N khác I
=> d3 đồng phẳng với d1, d2 : điều này xích míc !
Vậy d3 đồng quy với d1, d2 tại I .
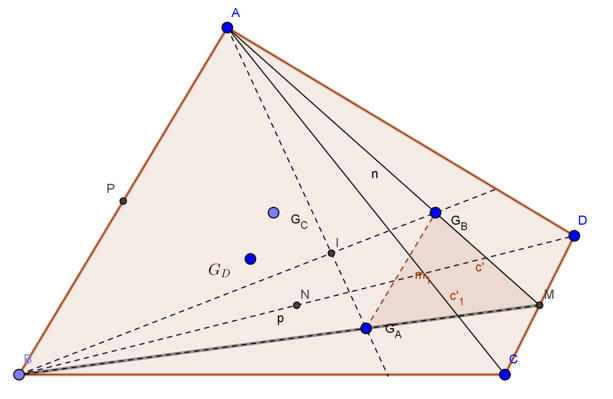
Bài 4 (trang 53 SGK Hình học 11): Cho bốn điểm A, B, C và D không đồng phẳng. Gọi GA, GB, GC, GD lần lượt là trọng tâm của các tam giác BCD, CDA, ADB, ACB. Chứng minh rằng AGA, BGB, CGC, DGD đồng qui.
Lời giải:
Gọi M, N, P. là trung điểm của CD, DB, BA .
Trong mp ( MAB ) : AGA ∩ BGB = I. Ta có :
Vậy ΔIAB đồng dạng với ΔIGAGB
Lại có ΔMAB đồng dạng với ΔMGBGA
Từ ( 1 ) và ( 2 ), ta có :
Chứng minh tương tự như, ta cũng có :
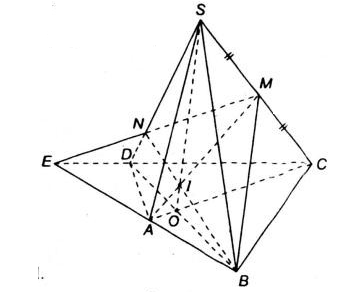
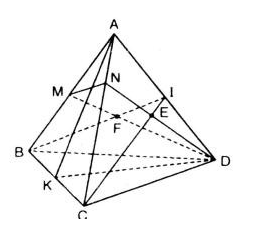
Bài 5 (trang 53 SGK Hình học 11): Cho tứ giác ABCD nằm trong mặt phẳng (α) có hai cạnh AB và CD không song song với nhau. S là điểm nằm ngoài mặt phẳng (α) và M là trung điểm của đoạn SC.
a ) Tìm giao điểm N của đường thẳng SD và mặt phẳng ( MAB ) .
b ) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM và BN đồng quy .
Cần nhớ
A ∈ d ⊂ mp ( α ) => A ∈ mp ( α )
Lời giải:
a ) Tìm N ∈ SD ∩ mp ( MAB )
Trong mp ( ABCD ), AB cắt CD tại E .
Trong mp ( SCD ), EM cắt SD tại N .
Ta có:
N ∈ SD
N ∈ EM ⊂ mp ( MAB )
Vậy N = SD ∩ mp ( MAB )
b ) Chứng minh SO, MA, BN đồng quy
Ta có :
* SO, MA, BN không ở trong cùng một mặt phẳng .
* SO và MA cắt nhau ( trong mp ( SAC ) )
MA và BN cắt nhau ( trong mp ( BEN ) )
BN và SO cắt nhau ( trong mp ( SBD ) )
Vậy SO, MA, BN đồng quy .
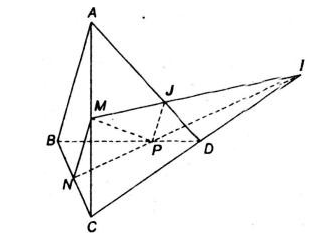
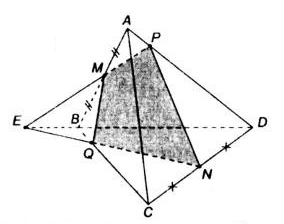
Bài 6 (trang 54 SGK Hình học 11): Cho bốn điểm A, B, C và D không đồng phẳng. Gọi M và N lần lượt là trung điểm của các đoạn thẳng AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a ) Tìm giao điểm của đường thẳng CD và mặt phẳng ( MNP ) .
b ) Tìm giao tuyến của hai mặt phẳng ( MNP ) và ( ACD ) .
Lời giải:
a ) Ta có :
=> NP và CD không song song với nhau .
=> NP và CD cắt nhau tại I .
I ∈ NP => I ∈ ( MNP ). Mà I ∈ CD : Vậy I ∈ CD ∩ ( MNP )
b ) Trong mặt phẳng ( ACD ) thì AD và MI cắt nhau tại điểm J :
J ∈ AD => J ∈ ( ACD )
J ∈ MI => J ∈ ( MNP )
Vậy J là một điểm chung của hai mặt phẳng ( ACD ) và ( MNP ) .
Ta đã có M là một điểm chung của hai mặt phẳng ( ACD ) và ( MNP ) .
Vậy MJ = ( ACD ) ∩ ( MNP ) .
Bài 7 (trang 54 SGK Hình học 11): Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
a ) Tìm giao tuyến của hai mặt phẳng ( IBC ) và ( KAD ) .
b ) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng ( IBC ) và ( DMN ) .
Lời giải:
a ) Tìm giao tuyến của mp ( IBC ) và mp ( KAD ) .
Ta có :
K ∈ BC => K ∈ ( IBC )
I ∈ AD => I ∈ ( KAD )
Vậy KI = ( IBC ) ∩ ( KAD )
b ) trong mp ( ABD ) : BI ∩ DM = F => F ∈ ( IBC ) ∩ ( DMN )
CI ∩ Doanh Nghiệp = E E ∈ ( IBC ) ∩ ( DMN )
Vậy ( IBC ) ∩ ( DMN ) = FE
Bài 8 (trang 54 SGK Hình học 11): Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD, trên cạnh AD lấy điểm P không trùng với trung điểm của AD.
a ) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng ( PMN ) và ( BCD ) .
b ) Tìm giao điểm của hia mặt phẳng ( PMN ) và BC .
Lời giải:
a ) Trong mp ( ABD ) : MP không song song với BD nên MP ∩ BD = E .
E ∈ MP => E ∈ ( PMN )
E ∈ BD => E ∈ ( BCD )
Nên E ∈ ( PMN ) ∩ ( BCD )
Nên EN = ( PMN ) ∩ ( BCD )
b ) Trong mp ( BCD ) : EN ∩ BC = Q. Mà ( PMN ) ≡ ( MEN ) ≡ ( MEQ )
Q ∈ ( MEQ ) ≡ ( PMN )
Mặt khác Q ∈ BC nên Q = BC ∩ ( PMN ) .
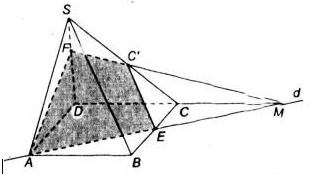
Bài 9 (trang 54 SGK Hình học 11): Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C’ là một điểm nằm trên cạnh SC.
a ) Tìm giao điểm M của CD và mp ( C’AE ) .
b ) Tìm thiết diện của hình chóp cắt bởi mặt phẳng ( C’AE ) .
Lời giải:
a ) Giao điểm M của CD và mp ( C’AE ) .
Trong mp ( ABCD ), d cắt CD tại M, ta có :
* M ∈ CD
* M ∈ d ⊂ ( C’AE )
M ∈ ( C’AE )
Vậy M là giao điểm của CD và mp ( C’AE ) .
b ) Thiết diện của hình chóp cắt bởi mp ( C’AE ) .
Trong mp ( SCD ), MC ’ cắt SD tại F .
Vậy thiết diện của hình chóp S.ABCD cắt bởi mp ( C’AE ) là tứ giác AFC’E .
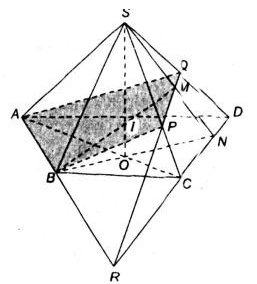
Bài 10 (trang 54 SGK Hình học 11): Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
a ) Tìm giao điểm N của đường thẳng CD và mp ( SBM ) .
b ) Tìm giao tuyến của hai mặt phẳng ( SBM ) và ( SAC ) .
c ) Tìm giao điểm I của đường thẳng BM và mặt phẳng ( SAC ) .
d ) Tìm giao điểm P. của SC và mặt phẳng ( ABM ), từ đó suy ra giao tuyến của hai mặt phẳng ( SCD ) và ( ABM ) .
Lời giải:
a ) Gọi N là giao điểm của SM và CD, thì N = CD ∩ ( SBM ) .
b ) Trong mp ( ABCD ), BN và AC cắt nhau tại điểm O .
O ∈ BN => O ∈ ( SBM )
O ∈ AC => O ∈ ( SAC )
=> O là một điểm chung của ( SBM )
và ( SAC ) .
Dễ thấy S cũng là một điểm chung của ( SBM ) và ( SAC ) .
Vậy SO = ( SBM ) ∩ ( SAC ) .
c ) Trong mp ( SBM ) thì BM và SO cắt nhau tại điểm I, ta có :
I ∈ BM I ∈ SO I ∈ ( SAC ). Vậy I = BM ∩ ( SAC ) .
d ) Trong mp ( SAC ), AI cắt SC tại O, ta có P ∈ SC và P ∈ AI .
=>P ∈ (ABM) hay P là giao điểm của mp(ABM) với cạnh SC của hình chóp.
Trong mp ( SCD ), PM cắt SD ở điểm Q., ta có Q ∈ SD ; Q ∈ PM nên PM ∈ ( ABM )
=> Q ∈ ( BM ) hay Q. là giao điểm của mp ( ABM ) với cạnh SD của hình chóp .
Vậy : ( SCD ) ∩ ( ABM ) = PQ .
Post navigation
Source: https://futurelink.edu.vn
Category: Tin tổng hợp