I. Định nghĩa về bất phương trình
1. Dạng tổng quát
f ( x ) g ( x ), f ( x ) ≤ g ( x ), f ( x ) ≥ g ( x )
Ví dụ cho BPT 4. x + 2 > 0 nghiệm đúng với mọi số thực x > − 0.5. Ta có tập nghiệm : x ∈ R | x | > − 0.5 = ( 0.5 ; ∞ )
2. Phương pháp giải bất phương trình lớp 10
* Bất phương trình bậc nhất một ẩn
Là bất phương trình dạng : a. x + b > 0
Trường hợp a # 0
– Nếu a > 0, tập nghiệm là :

– Nếu a < 0, tập nghiệm là :

Trường hợp a =0
– Nếu b > 0, Phương trình vô số nghiệm .
– Nếu b < 0, Phương trình vô nghiệm .
* Cách giải bất phương trình bậc 2 một ẩn
Là BPT dạng : a. x2 + b. x + c > 0 với a # 0
Đặt Δ = b2 − 4. a. c. Ta có những trường hợp sau :
– a < 0 thì BPT không nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là: ∅.
– a > 0 thì BPT nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là : R .
– a < 0 thì BPT không nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là : ∅ .
– a > 0 thì BPT nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là :
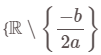
- Nếu Δ > 0, gọi x1, x2 (x1 < x2) là hai nghiệm của phương trình bậc hai a.x2 + b.x + c = 0 với

Khi đó :
– Nếu a > 0 thì tập nghiệm là : ( − ∞ ; x1 ) ∪ ( x2 ; + ∞ )
– Nếu a < 0 thì tập nghiệm là : ( x1 ; x2 )
II. Ví dụ về bất phương trình
Bài 1: Giải bất phương trình chứa căn sau:
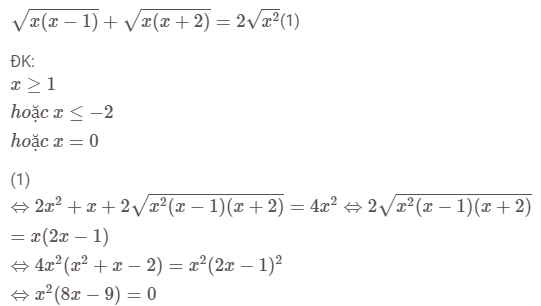
Vậy nghiệm của BPT là x = 0 hoặc x = 98
Bài 2: Tìm m để bất phương trình có nghiệm duy nhất:

III. Các bài tập giải bất phương trình lớp 10
Trong phần 2, chúng tôi xin trình làng những dạng bài tập vận dụng những công thức giải bất phương trình lớp 10. Các bài tập cũng được chia ra : bpt bậc nhất, bậc hai và những phương trình chứa dấu GTTĐ và chứa ẩn dưới dấu căn .
1. Bài tập về Bất phương trình :
Bài 1/ BPT bậc nhất


Bài 5/ BPT qui về bậc hai có chứa căn thức
Giải những phương trình sau :
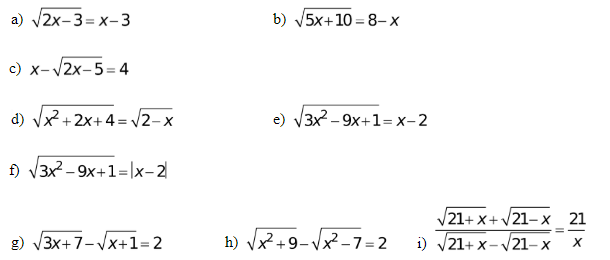
2. Bài tập về phương trình
3. Bài tập tổng hợp những dạng
Trên đây là những công thức giải bất phương trình lớp 10 và kèm theo là những dạng bài tập giải bất phương trình lớp 10. Để làm tốt dạng toán giải bất phương trình, trước hết những em học viên cần phải nắm vững những quy tắc xét dấu của tam thức bậc nhất và tam thức bậc hai. Sau đó, dựa vào những công thức mà tài liệu đã trình làng, những em hoàn toàn có thể vận dụng để giải những bất phương trình phức tạp hơn. Giải bất phương trình là một dạng toán rất quan trọng và theo suốt tất cả chúng ta trong chương trình toán THPT. Do đó, nó luôn Open trong những bài kiểm tra một tiết và đề thi học kì lớp 10 nên những em cần đặc biệt quan trọng chú ý quan tâm trong quy trình ôn tập. Hy vong, với những công thức mà Toploigiai trình làng, những bạn học viên lớp 10 sẽ thành thạo việc giải bất phương trình và đạt điểm trên cao trong những bài kiểm tra sắp tới .
Source: https://futurelink.edu.vn
Category: Tin tổng hợp