Câu C1 trang 86 SGK Vật Lý 10 Nâng Cao
Hãy nêu ý nghĩa của đại lượng k trong công thức ( 19.1 ) .
Giải :
Trong biểu thức Fđh = -k∆l, với cùng độ biến dạng, lò xo nào có k càng lớn thì lực đàn hồi càng lớn \(=>\) k đặc trưng cho khả năng tạo ra lực đàn hồi.
Câu C2 trang 86 SGK Vật Lý 10 Nâng Cao
Trên hình 19.5, ba lò xo khác nhau có cùng chiều dài tự nhiên. Khi những quả nặng như nhau được treo vào, độ biến dạng của những lò xo khác nhau. Lò xo nào có k lớn nhất ? Nêu ý nghĩa, đơn vị chức năng của k .
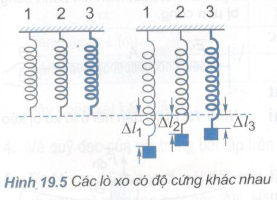
Giải :
H. 19.5 SGK cho \ ( \ Delta { l_1 } > \ Delta { l_2 } > \ Delta { l_3 } \ )
Áp dụng định luật Húc : \ ( \ eqalign { và P = \ left | { { F_ { dh } } } \ right | = { k_1 } \ Delta { l_1 } = { k_2 } \ Delta { l_2 } = { k_3 } \ Delta { l_3 } \ cr và = > \, { k_1 } < { k_2 } < { k_3 } \ cr } \ )
\ ( => \ ) lò xo có k càng lớn càng khó biến dạng, k càng nhỏ càng dễ biến dạng .
Vậy k đặc trưng cho tính dễ hay khó biến dạng của lò xo .
Đơn vị của k là N / m .
Bài 1 trang 88 SGK Vật Lý 10 Nâng Cao
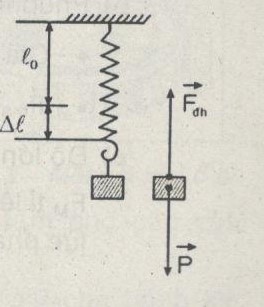
Trong thí nghiệm ở Hình 19.4, gọi độ cứng của lò xo là k, khối lượng vật nặng là m, tần suất rơi tự do là g. Độ dãn của lò xo nhờ vào vào những đại lượng nào ?
A. m, k .
B. k, g .
C. m, k, g .
D. m, g .
Giải :
Chọn C ( Khi đạt cân đối thì độ lớn :
\ ( { F_ { dh } } = P < = > k \ Delta l = mg = > \ Delta l = { { mg } \ over k } \ )
Độ dãn lò xo nhờ vào m, k, g ) .
Bài 2 trang 88 SGK Vật Lý 10 Nâng Cao
Phải treo một vật có khối lượng bằng bao nhiêu vào lò xo có độ cứng k = 100 N / m để lò xo dãn ra được 10 cm ?
Giải :
Ta có \ ( m = { { k \ Delta l } \ over g } = { { 100.0,1 } \ over { 9,8 } } \ approx 1,02 \, ( kg ). \ )
Bài 3 trang 88 SGK Vật Lý 10 Nâng Cao
Một xe hơi tải kéo một xe hơi con có khối lượng 2 tấn và chạy nhanh dần đều với tốc độ bắt đầu \ ( { v_0 } = 0 \ ). Sau 50 s đi được 400 m. Khi đó cáp nối hai xe hơi dãn ra bao nhiêu nếu độ cứng của nó là \ ( k = 2, { 0.10 ^ 6 } \, N / m \ ) ? Bỏ qua những lực cản công dụng lên xe hơi con .
Giải
Khi xe hơi tải chạy, dây cáp bị kéo căng, tính năng lực căng lên xe hơi con gây tần suất cho xe hơi con, vận dụng định luật II Niu – tơn và định luật Húc, ta có :
\ ( \ left. \ matrix { T = ma \ hfill \ cr T = k \ Delta l \ hfill \ cr } \ right \ } = > k \ Delta l = ma = > \ Delta l = { { ma } \ over k } \, ( 1 ) \ )
Ô tô con hoạt động nhanh dần đều không tốc độ đầu nên :
\ ( a = { { 2. S } \ over { { t ^ 2 } } } = { { 2.400 } \ over { 50 } } = 0,32 \, ( m / { s ^ 2 } ) \ )
Vậy \ ( \ Delta l = { { 2000.0,32 } \ over { 2, { { 0.10 } ^ 6 } } } = 3, { 2.10 ^ { – 4 } } ( m ) = 0,32 \, ( mm ) \ )
Bài 4 trang 88 SGK Vật Lý 10 Nâng Cao
Khi người ta treo quả cân có khối lượng 300 g vào đầu dưới của một lò xo ( đầu trên cố định và thắt chặt ), thì lò xo dài 31 cm. Khi treo thêm quả cân 200 g nữa thì lò xo dài 33 cm. Tính chiều dài tự nhiên và độ cứng của lò xo. Lấy \ ( g = 10 \, m / { s ^ 2 } \ ) .
Giải
Ta có :
\ ( \ eqalign { và { l_1 } – { l_0 } = \ Delta { l_1 } = { { { m_1 } g } \ over k } \, ( 1 ) \ cr và { l_2 } – { l_0 } = \ Delta { l_2 } = { { ( { m_1 } + { m_2 } ) g } \ over k } ( 2 ) \ cr } \ )
Lấy ( 2 ) – ( 1 ), được :
\ ( { l_2 } – { l_1 } = { { { m_2 } g } \ over k } \ )
\(= > k = {{{m_2}g} \over {{l_2} – {l_1}}} = {{0,2.10} \over {(33 – 31){{.10}^{ – 2}}}} = 100\,(N/m)\)
Từ ( 1 ) \ ( = > { l_0 } = { l_1 } – { { { m_1 } g } \ over k } = 0,31 – { { 0,3. 10 } \ over { 100 } } = 0,28 \, ( m ) \ )
\ ( = 28 \, cm \ )
Giaibaitap.me
Source: https://futurelink.edu.vn
Category: Tin tổng hợp